16637x

001513

Dipl.-Ing. (FH) Lukas Sühnel

04.04.2018

Tuyaux soumis à une pression interne

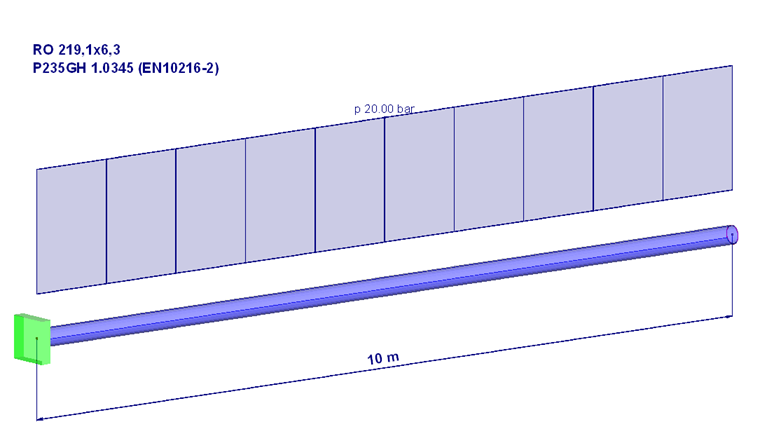
Les systèmes de canalisation sont exposés à un grand nombre de chargements. La pression interne est l’une des charges les plus déterminantes. Cet article décrit les contraintes et déformations résultantes d’une charge de pression intérieure pure dans la paroi du tuyau et pour le tuyau lui-même.

L’exemple suivant nous permet d’illustrer les explications de l’article.

Système

Le tuyau est considéré comme fermé des deux côtés. Ainsi, la pression est appliquée perpendiculaire à l’« aire de surface de la plaque de revêtement » interne.

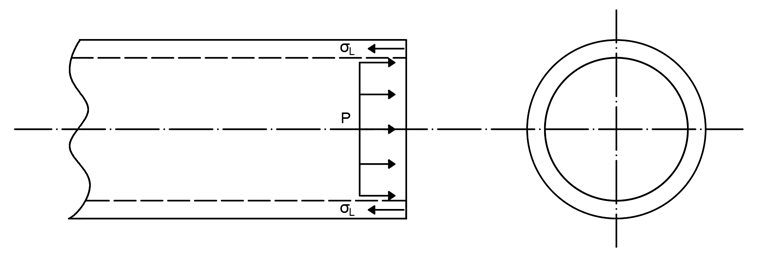
Contrainte longitudinale

Les forces résultantes doivent être absorbées par la paroi de tuyau. Ceci résulte d’une contrainte longitudinale pouvant être calculée comme suit :

σ_{l} = \frac{P \cdot r_{i}^{2}}{r_{e}^{2} - r_{i}^{2}}

Formule 1

où
r_i, r_e = rayons intérieur et extérieur

Autrement, la pression interne agit perpendiculaire à l’aire de surface de la paroi interne du tuyau. Ceci résulte de contraintes tangentielles et radiales pouvant être déterminées par les formules suivantes :

σ_{t} = P \cdot \frac{{(\frac{r_{e}}{r})}^{2} 1}{{(\frac{r_{e}}{r_{i}})}^{2} - 1}

Formule 2

σ_{r} = - P \cdot \frac{{(\frac{r_{e}}{r})}^{2} - 1}{{(\frac{r_{e}}{r_{i}})}^{2} - 1}

Formule 3

où
r = rayon aux limites r_i ≤ r ≤ r_e

Il est alors évident que les contraintes dépendent du rayon r considéré. L’autre conclusion est que ces contraintes sont réparties de manière non-uniforme sur la section. Toutefois, s’il s’agit de tuyaux à parois minces (diamètre extérieur/intérieur < 1,2), on peut supposer une distribution uniforme des contraintes. Les contraintes tangentielles et radiales sont alors les suivantes :

\begin{array}{l} {\bar{σ}}_{t} = \frac{P \cdot r_{i}}{r_{e} - r_{i}} \\ {\bar{σ}}_{r} = \frac{P \cdot r_{i}}{r_{e} r_{i}} \end{array}

Formule 4

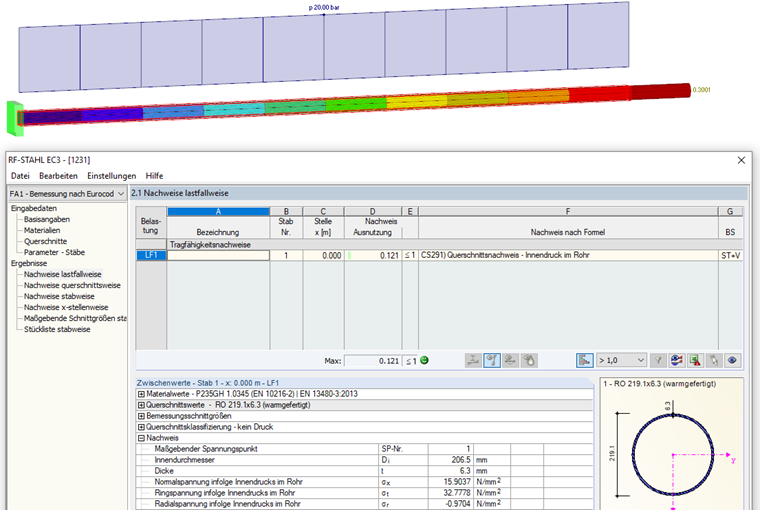
En entrant les valeurs initiales pour les paramètres, nous obtenons les contraintes suivantes :

\begin{array}{l} σ_{l} = \frac{2 \cdot 103, 25^{2}}{109, 55^{2} - 103, 25^{2}} = 15, 9 N / mm ² \\ {\bar{σ}}_{t} = \frac{2 \cdot 103, 25}{109, 55 - 103, 25} = 32, 8 N / mm ² \\ {\bar{σ}}_{r} = \frac{- 2 \cdot 103, 25}{109, 55 103, 25} = - 1, 0 N / mm ² \end{array}

Formule 5

Le changement de la longueur de tuyau résulte également de la pression interne. En général, la modification de la longueur est égale au produit de la longueur et de la déformation epsilon :
ΔL = L ∙ ε

La déformation du tuyau résulte des trois contraintes tout juste calculées :

ε = \frac{(σ_{l} - v \cdot (σ_{t} σ_{r}))}{E} = \frac{(15, 9 - 0, 3 \cdot (32, 8 - 1))}{212.000} = 3 \cdot 10^{- 5}

Formule 6

Ainsi, la modification de longueur est la suivante :
ΔL = 10.000 mm ∙ 3 ∙ 10^-5 = 0,3 mm

Les résultats, calculés à la main dans cet article, peuvent être reproduits dans RFEM (déformation) ou dans les modules pour la vérification de l’acier (contraintes).

Résultat

Pour la détermination des déformations, il est important d’activer l’effet Bourdon dans les paramètres globaux de calcul de RFEM. Si vous souhaitez ne pas considérer ni les contraintes axiales des tuyaux, ni l’allongement des coudes, utilisez le module additionnel RF-PIPING.

Littérature

[1]	Franke, W.; Platzer, B. : Principes de base de la tuyauterie - Planification - Assemblage. Munich : Carl Hanser, 2014
[2]	Wikipédia : Formule de Barlow (en anglais)

Auteur

M. Sühnel est responsable de l'assurer de la qualité de RSTAB ; il participe également au développement de produits et fournit un support technique pour nos clients.

Liens

Modules additionnels de RFEM 5 - Systèmes de tuyauterie

Téléchargements

Fichier du modèle RFEM

2,38 MB

;