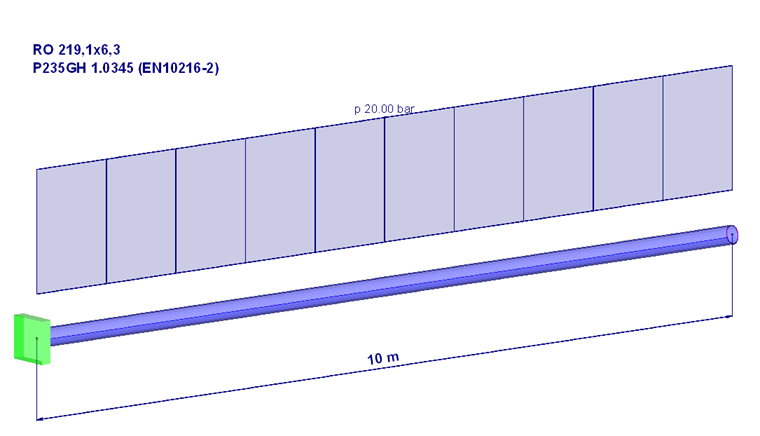
Zur Nachvollziehbarkeit wird folgendes Beispiel verwendet.
Das Rohr wird hierbei als an beiden Seiten geschlossen betrachtet. Dadurch wird einerseits ein Druck senkrecht auf die innere "Deckelfläche" ausgeübt.
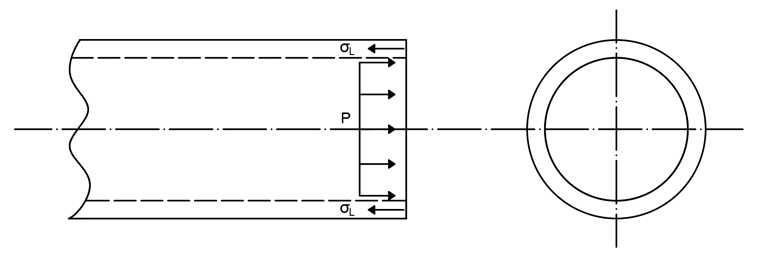
Die dadurch entstehende Kraft muss wiederum von der Rohrwandung aufgenommen werden. Dies hat eine Längsspannung zur Folge, die wie folgt berechnet werden kann:
mit
ri, re = Innen- und Außenradius
Andererseits wirkt der Innendruck senkrecht auf die Rohrinnenwand. Dies hat eine Tangential- sowie Radialspannung zur Folge, die mittels der folgenden Formeln bestimmt werden können:
mit
r = Radius in den Grenzen ri ≤ r ≤ re
Es wird ersichtlich, dass die Spannungen vom betrachteten Radius r abhängen. Dies bedeutet im Umkehrschluss, dass diese ungleichmäßig über den Querschnitt verlaufen. Für dünnwandige Rohre (Außendurchmesser/Innendurchmesser < 1,2) kann jedoch eine gleichmäßige Spannungsverteilung angenommen werden. Damit ergeben sich die mittlere Tangential- beziehungsweise Radialspannung zu:
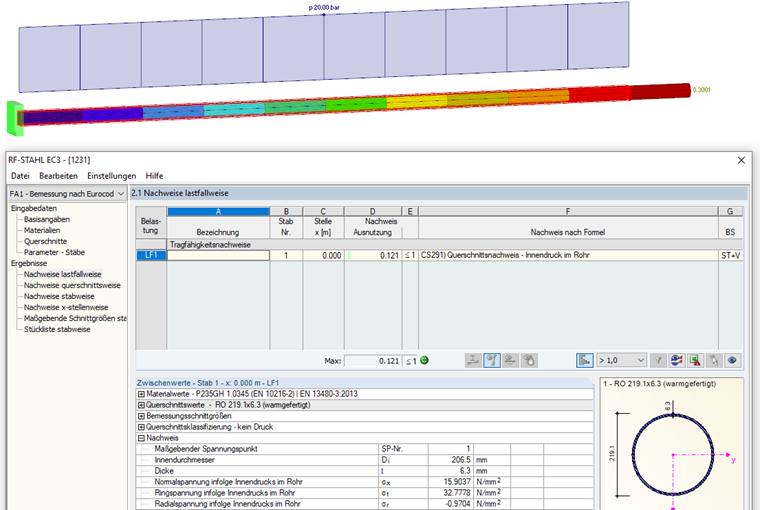
Setzt man die Eingangswerte in die Formeln ein, erhält man folgende Spannungen:
Aus dem Innendruck folgt ebenso eine Längenänderung des Rohres. Allgemein formuliert ist die Längenänderung gleich dem Produkt der Länge mit der Dehnung Epsilon:
ΔL = L ∙ ε
Die Dehnung des Rohres ergibt sich aus den drei soeben berechneten Spannungen:
Die Längenänderung beträgt daher:
ΔL = 10.000 mm ∙ 3 ∙ 10-5 = 0,3 mm
Die hier händisch berechneten Ergebnisse können auch in RFEM (Verformung) beziehungsweise den Stahl-Bemessungsmodulen (Spannungen) nachvollzogen werden.
Wichtig für die Verformung ist die Aktivierung des Bourdon-Effekts in den globalen Berechnungsparametern von RFEM. Möchte man nicht nur die axiale Dehnung von Rohren berücksichtigen, sondern auch die Aufweitung von Rohrbögen, ist auf das Zusatzmodul RF-PIPING zurückzugreifen.
Literatur