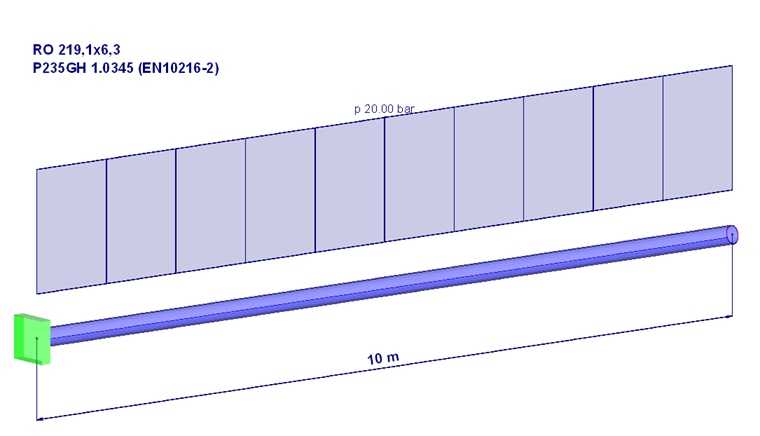
Para una compresión mejor, se usa el ejemplo siguiente.
El tubo se considera cerrado en ambos lados. Por una parte, se aplica la presión perpendicular al "superficie interna de la placa de la tapa".
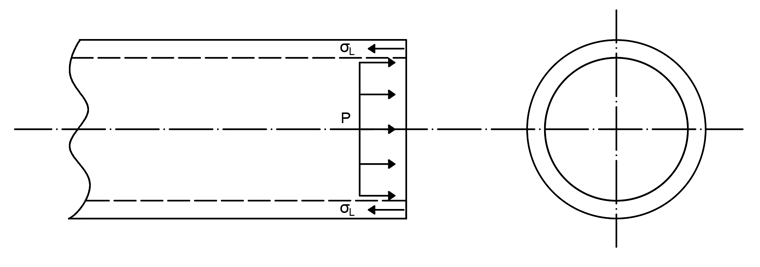
La fuerza que surge debe ser absorbida por la pared de la tubería. Esto resulta en una tensión longitudinal que puede ser calculada como sigue:
Donde
ri, re = radio interior y exterior
Por otra parte, la presión interna actúa perpendicular al área de la superficie de la pared del tubo. Esto resulta en una tensión tangencial y también radial que pueden determinarse por las fórmulas siguientes:
Donde
r = radio en los límites ri ≤ r ≤ re
Se puede ver que las tensiones dependen del radio r considerado. Esto implica, a la inversa, que estos corren de manera desigual a lo largo de la sección transversal. Sin embargo, para los tubos de paredes delgadas (diámetro exterior/diámetro interior <1,2), se puede suponer una distribución uniforme de la tensión. Por tanto, las tensiones tangenciales y radiales medias son las siguientes:
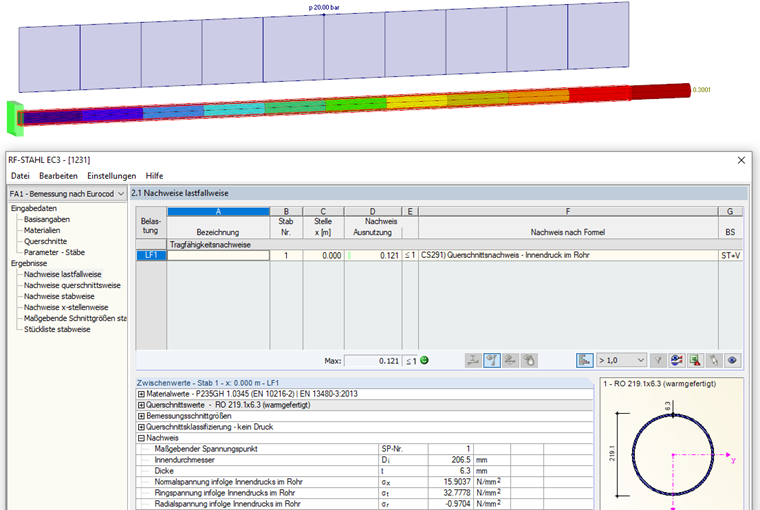
Estableciendo los valores iniciales en las fórmulas, obtenemos las tensiones siguientes:
Un cambio en la longitud del tubo también resulta de la presión interna. Hablando en general, el cambio en la longitud es igual al producto de la longitud y la deformación epsilon:
ΔL = L ∙ ε
La deformación de los tubos resulta de las 3 tensiones calculadas anteriormente:
Por tanto, el cambio en la longitud es el siguiente:
ΔL = 10 000 mm ∙ 3 ∙ 10-5 = 0,3 mm
Los resultados, los cuales están calculados manualmente en este artículo, se pueden reproducir también en RFEM (deformación) o en los módulos de cálculo de acero (tensiones).
Para la deformación es importante activar el efecto Bourdon en los parámetros de cálculo generales de RFEM. Si no sólo quiere considerar la deformación axial de tubos sino también el alargamiento de las curvas de tubos, use el módulo adicional RF-PIPING.
Bibliografía