13910x

Dipl.-Ing. (FH) Lukas Sühnel

2018-04-04

管道结构受内部压力作用

管道结构系统通常所受的荷载形式较多。其中最重要的荷载就是管道内部的压力荷载。本篇专题将阐述管道在内部压力荷载作用下管道和管道壁的应力和变形计算。

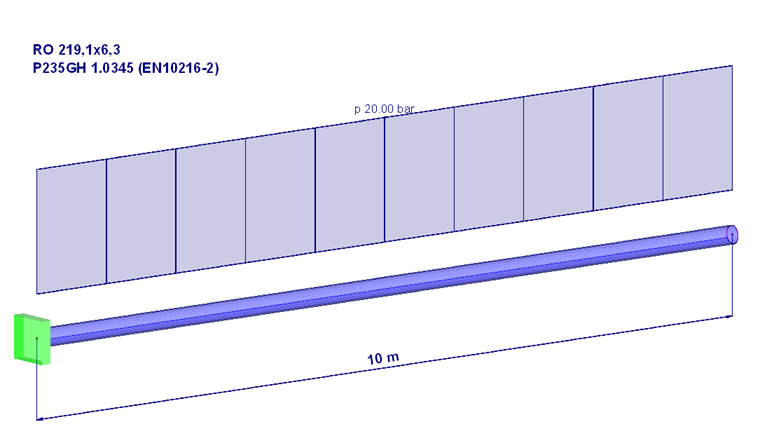
为了便于完全理解可以参考下面的例题。

System

例题中管道结构的两端为封闭状态。那么可以在管道的一端将压力垂直作用于管道内部的“盖板平面”。

Längsspannung

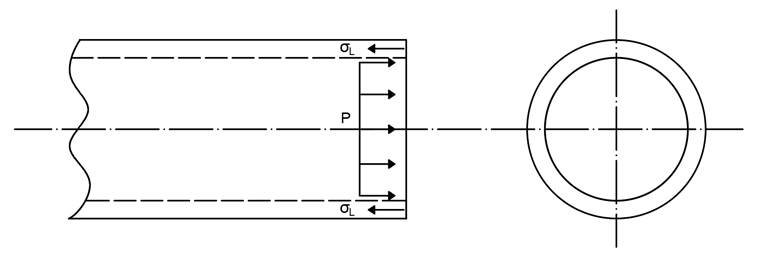
上述压力产生的荷载必须通过由管道壁产生的反力抵消。管道壁中的纵向应力可以按照下列方法进行计算：

σ_{l} = \frac{P \cdot r_{i}^{2}}{r_{e}^{2} - r_{i}^{2}}

公式 1

值:
r_i, r_e = 内部和外部半径

另外一个方面由管道内部压力可以产生垂直于管道内壁的作用。此作用可以产生切向和径向的应力，具体应力数值可以按照下列方法进行计算：

σ_{t} = P \cdot \frac{{(\frac{r_{e}}{r})}^{2} 1}{{(\frac{r_{e}}{r_{i}})}^{2} - 1}

公式 2

σ_{r} = - P \cdot \frac{{(\frac{r_{e}}{r})}^{2} - 1}{{(\frac{r_{e}}{r_{i}})}^{2} - 1}

公式 3

值:
r = 半径范围内 r_i ≤ r ≤ r_e

可以看出，应力与考虑的半径 r 相关。反之，这意味着它们在截面上的延伸是不均匀的。对于薄壁管（外径/内径 < 1.2），可以假设应力分布是均匀的。由此可以得出切向和径向应力的数值为：

\begin{array}{l} {\bar{σ}}_{t} = \frac{P \cdot r_{i}}{r_{e} - r_{i}} \\ {\bar{σ}}_{r} = \frac{P \cdot r_{i}}{r_{e} r_{i}} \end{array}

公式 4

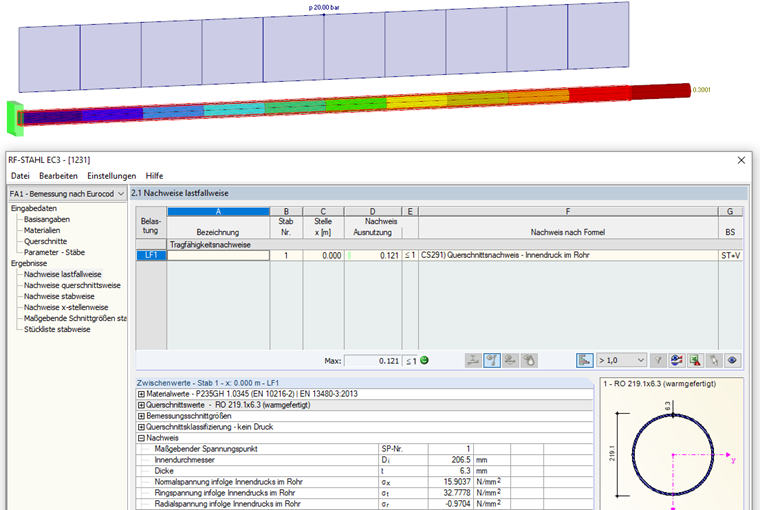
带入初始的数据后，得出应力值为：

\begin{array}{l} σ_{l} = \frac{2 \cdot 103, 25^{2}}{109, 55^{2} - 103, 25^{2}} = 15, 9 N / mm ² \\ {\bar{σ}}_{t} = \frac{2 \cdot 103, 25}{109, 55 - 103, 25} = 32, 8 N / mm ² \\ {\bar{σ}}_{r} = \frac{- 2 \cdot 103, 25}{109, 55 103, 25} = - 1, 0 N / mm ² \end{array}

公式 5

由管道内部压力同样会产生管道的纵向长度变化。一般的计算表达式为，纵向长度变化等于长度乘以线应变 Epsilon：
ΔL = L ∙ ε

管道的线应变可以由上述相关的三个应力进行计算：

ε = \frac{(σ_{l} - v \cdot (σ_{t} σ_{r}))}{E} = \frac{(15, 9 - 0, 3 \cdot (32, 8 - 1))}{212.000} = 3 \cdot 10^{- 5}

公式 6

纵向长度变化等于：
ΔL = 10,000 mm ∙ 3 ∙ 10^-5 = 0.3 mm

进行比较后，例题中手算的计算结果与在有限元软件 RFEM（变形）以及钢结构附加模块（应力）的计算结果也相符。

结果

计算时需要注意在 RFEM 软件中激活全局基本计算参数中的管道应力分析需考虑的波登效应（Bourdon 效应）选项。如果不仅要计算管道轴向的线应变而且还需要考虑弯管的扩张，那么就需要使用附加模块 RF-PIPING 进行计算。

使用的文献材料

[1]	弗兰卡，W. Platzer, B.: 管道基础 - 设计 - 安装。慕尼黑：卡尔·汉瑟，2014
[2]	维基百科:锅炉公式

作者

Sühnel 先生目前主要负责 RSTAB 的质量保证部门；同时还参与产品开发，为客户提供技术支持。

链接

RFEM 5 附加模块 - 管道系统

下载

RFEM Model File

2.38 MB

您有什么问题想问的吗？

视频

知识库

知识库知识库 | 使用自由线荷载生成杆件荷载

长度: 00:00:38 min

知识库

KB 000712 | 管道面建模

长度: 00:00:31 min

知识库

知识库 000670 | 保存和导入杆端铰图表

长度: 00:00:34 min

常见问题和解答 (FAQ)

[ZH] 常见问题 004830 | 如何激活管道建模？

长度: 00:00:19 min

常见问题和解答 (FAQ)

[ZH] FAQ 001062 | 我已经计算了一个箱形梁。哪个面产生或面应力...

长度: 00:01:00 min

活动

RFEM中的板壳建模-第2部分

长度: 01:06:55 min

活动

RFEM中的板壳建模-第1部分

长度: 01:06:05 min

常见问题和解答 (FAQ)

FAQ 004165 | 如何考虑杆件单元的真实截面几何形状...

长度: 00:00:22 min

常见问题和解答 (FAQ)

FAQ 004159 | 我想要创建一个由多个部分组成的环形管道。如何防止...

长度: 00:01:13 min

播放列表

下载模型

347x

25x

管道 - U 形补偿器

817x

53x

钢筋混凝土箱形涵洞

464x

双下水道涵洞

853x

13x

双涵洞

592x

12x

混凝土涵洞

1255x

漏斗板

445x

17x

欧米茄管

772x

50x

法兰和弯头的连接

566x

39x

管道缩减

知识库文章

了解更多

Nicht alle Strukturelemente des realen Bauwerks werden im statischen Modell herangezogen. Als Beispiel hierfür soll eine Rohrleitung dienen, die auf einem Stahlträgergerüst verläuft.

了解更多

Speziell im Anlagenbau, aber auch bei der Detailbetrachtung von statischen Strukturen kann es notwendig werden, Rohrquerschnitte als Flächenmodelle analysieren zu müssen. Für diese Zwecke bietet RFEM die Möglichkeit, anhand einer Linie automatisch Rohrquerschnitte zu erzeugen.

了解更多

In RFEM 5 und RSTAB 8 können Stabendgelenken Nichtlinearitäten zugeordnet werden. Es steht hierbei neben den Nichtlinearitäten "Fest, falls..." und "Teilweise Wirkung..." auch "Diagramm..." zur Verfügung. Wählt man die Option "Diagramm...", sind im zugehörigen Dialog die entsprechenden Einstellungen für die Wirkung des Stabendgelenks einzutragen. Hierbei sind für die einzelnen Definitionspunkte die Abszissen- und Ordinatenwerte (Verformungen beziehungsweise Verdrehungen und zugehörige Schnittgrößen) einzutragen, welche das Gelenk definieren.