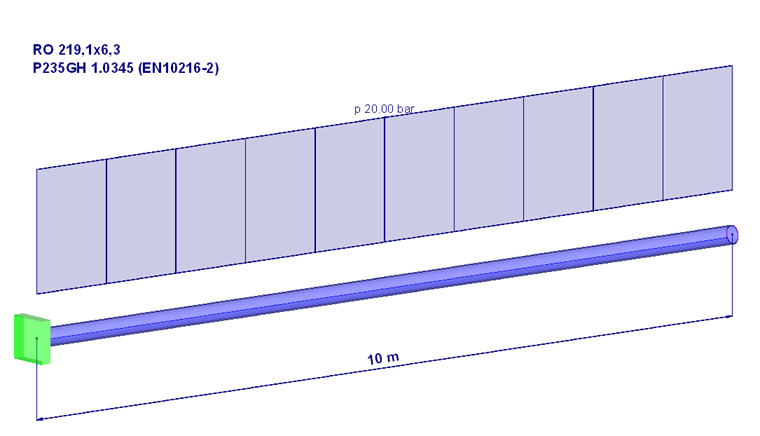
Zrozumienie zjawiska ułatwia poniższy przykład.
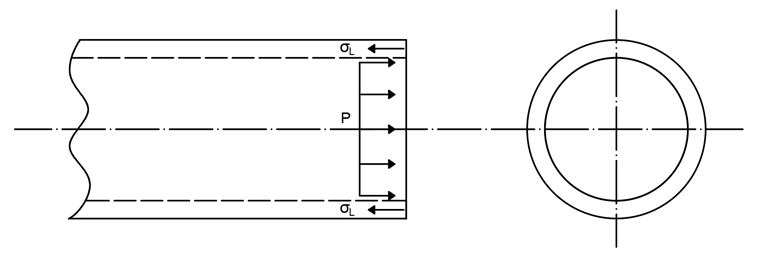
Zakłada się, że rura jest zamknięta po obu stronach. Z jednej strony, ciśnienie zostaje przyłożone prostopadle do wewnętrznego “obszaru powierzchni pokrywy”.
Rosnąca siła musi zostać przeniesiona przez ścianę rury. Skutkuje to powstaniem naprężenia wzdłużnego, obliczanego następująco:
Gdzie
ri, re = promień wewnętrzny i zewnętrzny
Z drugiej strony, ciśnienie wewnętrzne działa prostopadle do obszaru powierzchni ściany rury. To z kolei powoduje powstanie naprężenia stycznego oraz promieniowego, które może zostać określone z użyciem poniższych wzorów:
Gdzie
r = promień w granicach ri ≤ r ≤ re
Jak widać, naprężenia zależą od rozpatrywanego promienia r. To z kolei implikuje, że przebiegają one nierównomiernie w poprzek przekroju. W przypadku rur cienkościennych (średnica zewnętrzna/średnica wewnętrzna < 1,2) można jednak założyć równomierny rozkład naprężeń. Tak więc, średnie naprężenie styczne i promieniowe wynosi:
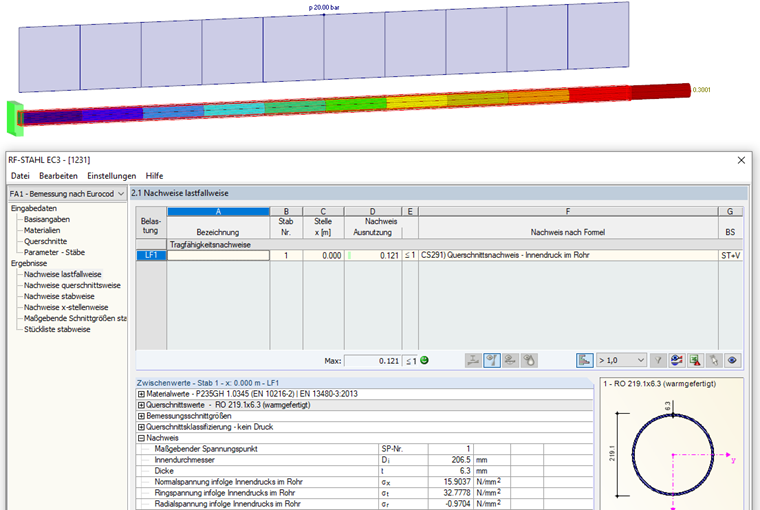
Wstawiając wartości początkowe do wzorów, otrzymujemy następujące naprężenia:
Zmiana długości rury także wynika z ciśnienia wewnętrznego. Mówiąc ogólnie, zmiana długości jest równa iloczynowi długości rury i odkształcenia epsilon:
ΔL = L ∙ ε
Odkształcenie rury wynika z trzech wartości naprężeń obliczonych powyżej:
Tak więc, zmiana długości jest następująca:
ΔL = 10,000 mm ∙ 3 ∙ 10-5 = 0.3 mm
Wyniki, które w niniejszym artykule są obliczane ręcznie, można także odtworzyć w programie RFEM (w zakresie odkształcenia) lub w modułach do analizy konstrukcji stalowych (naprężenia).
W przypadku analizy odkształcenia, ważne jest aktywowanie w ogólnych parametrach obliczeniowych programu RFEM efektu Bourdon’a. Jeżeli uwzględniane ma być nie tylko odkształcenie osiowe rur, lecz także ich rozszerzania się na zakrętach rury, należy skorzystać z modułu dodatkowego RF-PIPING.
Literatura