7047x

001669

Dipl.-Ing. (FH) Gerhard Rehm

2020-12-18

Потеря устойчивости плоской формы изгиба в деревянных конструкциях | Примеры 2

Предыдущая статья Потеря устойчивости плоской формы изгиба в деревянных конструкциях | В примере 1 на простых примерах поясняется практическое применение расчета критического изгибающего момента M_crit или критического изгибающего напряжения σ_crit при продольном изгибе изогнутой балки. В нашей статье критический изгибающий момент будет найден с учетом упругого основания при наличии связи жесткости.

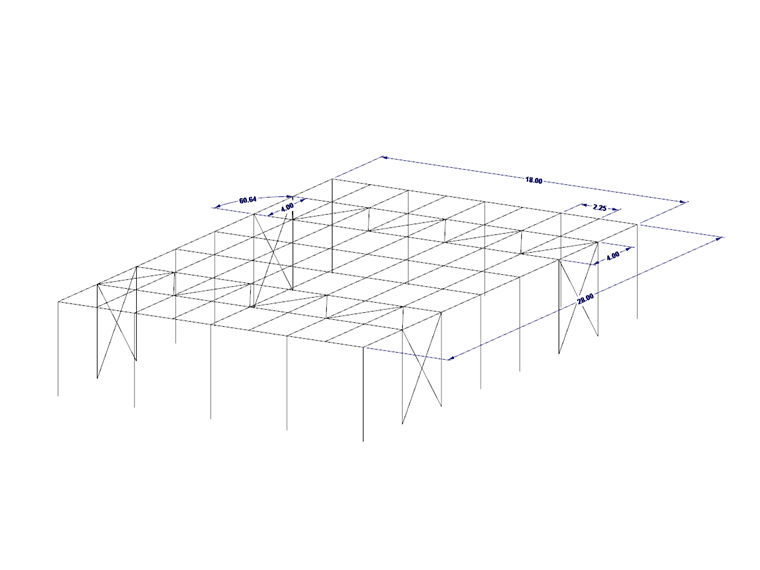
Конструктивная модель

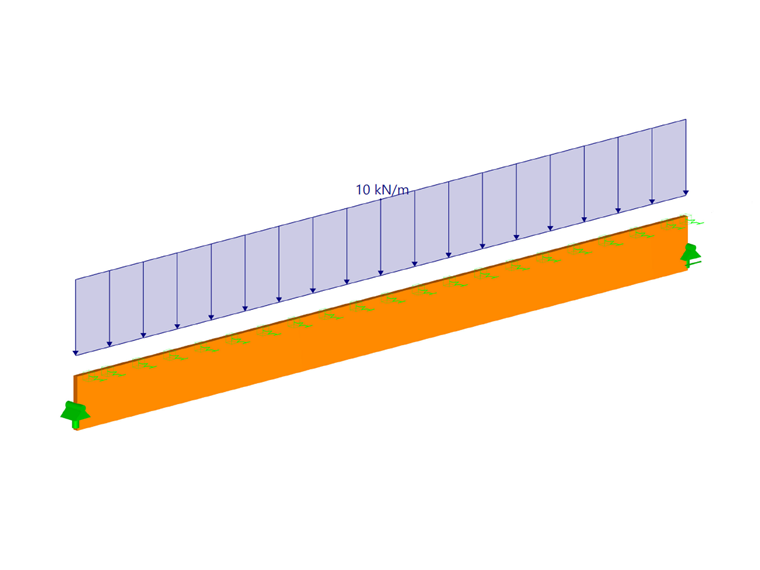
Для конструкции, показанной на Рисунке 01, необходимо выполнить расчет стропильной фермы на боковое выпучивание. На уровне кровли размещены шесть ферм в качестве параллельных балок длиной 18 м с двумя связями жесткости. Балки по сторонам фронтона опираются на колонны и не учитываются в расчете. На фермы действует расчетная нагрузка q_d, равная 10 кН/м.

1 Конструктивная модель

Данные о модели

Result of Eigenvalue Analysis for Single-Span Beam With Lateral and Torsional Restraint without Intermediate Supports	18	m	Длина балки
b	120	мм	Ширина балки
h	1,200	мм	Высота балки
GL24h	-	-	Материал по норме EN 14080
i_Z	172.800.000	мм⁴	Момент инерции
I_T	647.654.753	мм⁴	момент инерции при кручении
q_d	10	кН/м	Расчетная нагрузка
a_z	600	мм	Положение нагрузки
e	600	мм	Положение фундамента

Внимание! Несмотря на то, что следующие уравнения E и G не ссылаются прямо на значения 5% квантиля в индексе, они были соответственно приняты во внимание.

Однопролетная балка с вильчатым опиранием без промежуточных опор

2 Однопролетная балка с вильчатым опиранием без промежуточных опор

Для полноты мы сначала проанализируем стропильную ферму без боковых опор (см. Рисунок 02). Длина заменяемого стержня в случае приложения нагрузки с верхней стороны фермы при a₁ = 1,13 и a₂ = 1,44 равна:

l_{ef} = \frac{L}{a_{1} \cdot (1 - a_{2} \cdot \frac{a_{z}}{L} \cdot \sqrt{\frac{E_{0, 05} \cdot I_{Z}}{G_{0, 05} \cdot I_{T}}})}

l_ef	Ersatzstablänge
L	Trägerlänge, Abstand der seitlichen Halterung
a₁,a₂	Kippbeiwerte
a_z	Abstand des Lastangriffs vom Schubmittelpunkt
E_0,05	5 % Quantile des Elastizitätsmoduls
G_0,05	5 % Quantile des Schubmoduls
I_z	Trägheitsmoment um die schwache Achse
I_T	Torsionsträgheitsmoment

Длина эквивалентного стержня

l_ef = 17,79 м

После этого мы можем рассчитать значение критического изгибающего момента следующим образом:

M_{crit} = \frac{π \cdot \sqrt{E_{0, 05} \cdot I_{Z} \cdot G_{0, 05} \cdot I_{tor}}}{l_{ef}}

M_crit	Kritisches Biegemoment
E_0,05	5 % Quantile des Elastizitätsmoduls
G_0,05	5 % Quantile des Schubmoduls
I_z	Trägheitsmoment um die schwache Achse
I_T	Torsionsträgheitsmoment
l_ef	Ersatzstablänge

Критический изгибающий момент

M_crit = 134,52 кНм

В наших примерах мы не будем рассматривать увеличение произведения 5% квантилей параметров жесткости в результате гомогенизации балок из клееной древесины.

Изгибающий момент, действующий на фермы, равен:

M_{d} = \frac{q_{d} \cdot L^{2}}{8}

M_d	Bemessungsmoment
q_d	Bemessungslast
L	Trägerlänge

Расчетный момент

M_d = 405,00 кНм

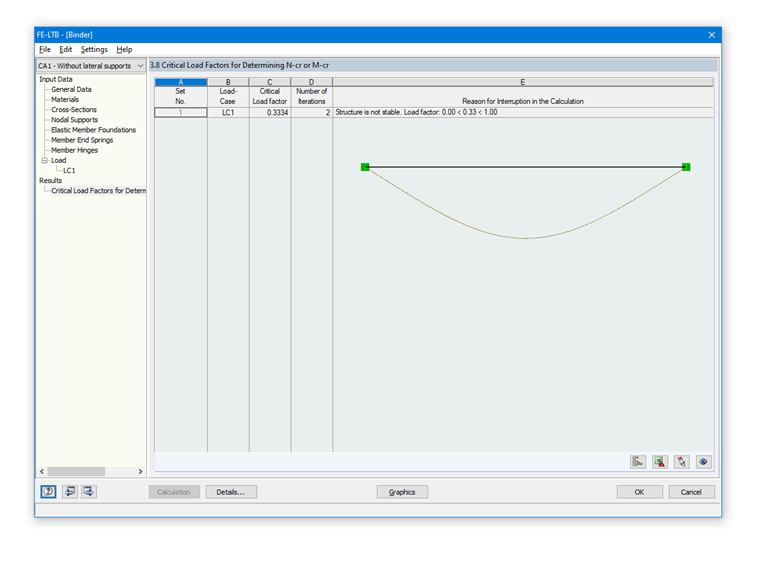
В результате анализа собственных чисел в дополнительном модуле RF-/FE-LTB мы получим коэффициент критической нагрузки, равный 0,3334. На основе этого критический изгибающий момент равен

M_crit = 0,3334 ⋅ 405 кНм = 135,03 кНм

и, таким образом, идентичен результату аналитического решения.

Результаты расчета методом собственных чисел у однопролетной балки с вильчатым опиранием без промежуточных опор

3 Result of Eigenvalue Analysis for Single-Span Beam With Lateral and Torsional Restraint without Intermediate Supports

Как и следовало ожидать, у такой тонкой фермы без опор действующий изгибающий момент больше (в 3 раза), чем критический изгибающий момент, и, таким образом, ферма недостаточно защищена от потери устойчивости. Вместе с тем, этому должна противостоять связь, которую мы теперь введем в расчет.

Однопролетная балка с вильчатым опиранием и жесткими промежуточными опорами

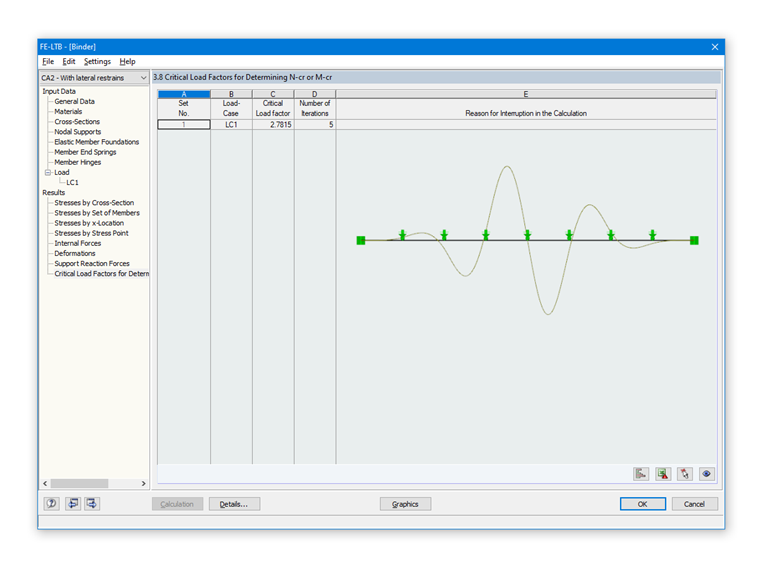
4 Однопролетная балка с вильчатым опиранием и жесткими промежуточными опорами

Если связь обладает достаточной жесткостью, то на практике в качестве длины заменяемого стержня в расчете потери устойчивости часто применяется расстояние между боковыми опорами (например, прогонами). Данный порядок был пояснен в предыдущей статье «Потеря устойчивости плоской формы изгиба в деревянных конструкциях». | Примеры 1

Потеря устойчивости плоской формы изгиба в деревянных конструкциях | Примеры 1

Таким образом, в качестве длины L применяется значение 2,25 м. При a₁ = 1,00 и a₂ = 0,00 мы получим:

l_{ef} = \frac{L}{a_{1} \cdot (1 - a_{2} \cdot \frac{a_{z}}{L} \cdot \sqrt{\frac{E_{0, 05} \cdot I_{z}}{G_{0, 05} \cdot I_{T}}})}

l_ef	Ersatzstablänge
L	Trägerlänge, Abstand der seitlichen Halterung
a₁,a₂	Kippbeiwerte
a_z	Abstand des Lastangriffs vom Schubmittelpunkt
E_0,05	5 % Quantile des Elastizitätsmoduls
G_0,05	5 % Quantile des Schubmoduls
I_z	Trägheitsmoment um die schwache Achse
I_T	Torsionsträgheitsmoment

Длина эквивалентного стержня

l_ef = 2,25 м

Критический изгибающий момент равен:

M_{crit} = \frac{π \cdot \sqrt{E_{0, 05} \cdot I_{Z} \cdot G_{0, 05} \cdot I_{tor}}}{l_{ef}}

M_crit	Kritisches Biegemoment
E_0,05	5 % Quantile des Elastizitätsmoduls
G_0,05	5 % Quantile des Schubmoduls
I_z	Trägheitsmoment um die schwache Achse
I_T	Torsionsträgheitsmoment
l_ef	Ersatzstablänge

Критический изгибающий момент

M_crit = 1063,51 кНм

Поскольку изгибающий момент, действующий на балку, меньше критического изгибающего момента, балка не подвержена потере устойчивости при наличии жестких промежуточных опор.

В результате анализа собственных чисел в дополнительном модуле RF-/FE-LTB мы получим коэффициент критической нагрузки, равный 2,7815. На основе этого критический изгибающий момент равен

M_{crit} = η \cdot M_{d}

M_crit	Kritisches Biegemoment
η	Verzweigungslastfaktor
M_d	Bemessungsmoment

Критический изгибающий момент

M_crit = 2,7815 ⋅ 405 кНм = 1 126,50 кНм

5 Результаты расчета методом собственных чисел у однопролетной балки с вильчатым опиранием и жесткими промежуточными опорами

Однопролетная балка с вильчатым опиранием и упругим основанием стержня

Как при потере устойчивости плоской формы изгиба в деревянных конструкциях | теории, нахождение эквивалентных длин стержня расширено коэффициентами α и β для стержней с упругим основанием в [1].

Потеря устойчивости плоской формы изгиба в деревянных конструкциях | Способ расчёта

Таким образом можно принять во внимание сдвиговую жесткость связи в потере устойчивости фермы. Жесткость связи при сдвиге' можно определить, например, по {%><#Refer [2]]] рисунку 6.34. Как мы видим, она зависит от типа связи, жесткости при растяжении подкосов и стоек, наклона подкосов и податливости соединительных элементов. Для связи, показанной на Рисунке 01, жесткость при сдвиге равна:

s_{id} = E_{D} \cdot A_{D} \cdot \sin {(α)}^{2} \cdot \cos (α)

s_id	Ideelle Schubsteifigkeit des Aussteifungsverbandes
E_D	5 % Quantile des Elastizitätsmoduls der Diagonalen
A_D	Querschnittsfläche der Diagonalen
α	Winkel zwischen der Diagonalen und der Gurte

Идеальная жесткость поперечной связи

При этом E_D - модуль упругости подкосов, а A_D - площадь их сечения. Однако в указанное выше уравнение не входит податливость соединительных элементов подкосов. Податливость, а также удлинение стержней подкосов можно учесть с помощью фиктивной площади сечения A_D'. Из этого следует:

s_{id} = E_{D} \cdot A_{D}' \cdot \sin {(α)}^{2} \cdot \cos (α)

s_id	Ideelle Schubsteifigkeit des Aussteifungsverbandes
E_D	5 % Quantile des Elastizitätsmoduls der Diagonalen
A_D'	Fiktive Querschnittsfläche der Diagonalen
α	Winkel zwischen der Diagonalen und der Gurte

Идеальная жесткость поперечной связи

Где:

A_{D}' = \frac{A_{D}}{1 + \frac{E_{D} \cdot A_{D}}{L_{D}} \cdot \sum \frac{1}{K_{ser}}}

A_D'	Fiktive Querschnittsfläche der Diagonalen
A_D	Querschnittsfläche der Diagonalen
E_D	5 % Quantile des Elastizitätsmoduls der Diagonalen
L_D	Länge der Diagonalen
K_ser	Verschiebungsmodul der Verbindung

Условная площадь сечения диагоналей

Подкосы имеют размер w/h = 120/200 мм и длину L_D 4,59 м. Модуль смещения соединения с каждой стороны подкоса должен составлять 110 000 Н/мм.

Идеальная площадь равна соответственно

A_D' = 12 548 мм²

и, следовательно, жесткость связи при сдвиге с углом подкоса относительно пояса 60,64 °

s_{id} = E_{D} \cdot A_{D}' \cdot \sin {(α)}^{2} \cdot \cos (α)

s_id	Ideelle Schubsteifigkeit des Aussteifungsverbandes
E_D	5 % Quantile des Elastizitätsmoduls der Diagonalen
A_D'	Fiktive Querschnittsfläche der Diagonalen
α	Winkel zwischen der Diagonalen und der Gurte

Идеальная жесткость поперечной связи

s_id = 44 864 кН

Основание стержня для каждой связи можно преобразовать по формуле {%ref#Refer [2]]] 7.291 следующим образом:

K_{y}' = s_{id} \cdot \frac{π^{2}}{L^{2}}

K_{y}' = 44.864 kN \cdot \frac{π^{2}}{{(18 m)}^{2}} = 1.367 \frac{kN}{m^{2}} = 1, 367 \frac{N}{{mm}^{2}}

K_y'	Elastische Stabbettung pro Verband
s_id	Ideelle Schubsteifigkeit des Aussteifungsverbandes
L	Länge des Verbandes

Упругое основание стержня на отдельных связях

Для двух связей и шести ферм можно применить следующую константу упругости для каждой фермы:

K_{y} = \frac{2 \cdot K_{y}'}{6}

K_y	Elastische Stabbettung pro Binder
K_y'	Elastische Stabbettung pro Verband

Упругое основание стержня на отдельные фермы

K_y = 455,6 кН/м² = 0,456 Н/мм²

При условии, что K_G = ∞, K_θ = 0, K_y = 0,456 Н/мм², e = 600 мм, a₁ = 1,13 и a₂ = 1,44, длина заменяемого стержня равна:

l_{ef} = \frac{L}{a_{1} \cdot (1 - a_{2} \cdot \frac{a_{z}}{L} \cdot \sqrt{\frac{E_{0, 05} \cdot I_{z}}{G_{0, 05} \cdot I_{T}}})} \cdot \frac{1}{α \cdot β}

l_ef	Ersatzstablänge
L	Trägerlänge, Abstand der seitlichen Halterung
a₁,a₂	Kippbeiwerte
a_z	Abstand des Lastangriffs vom Schubmittelpunkt
E_0,05	5 % Quantile des Elastizitätsmoduls
G_0,05	5 % Quantile des Schubmoduls
I_z	Trägheitsmoment um die schwache Achse
I_T	Torsionsträgheitsmoment
α, β	Beiwerte zur Berücksichtigung einer Stabbettung

Длина эквивалентного стержня

l_ef = 0,13

Критический изгибающий момент в результате равен утопическому значению:

M_{crit} = \frac{π \cdot \sqrt{E_{0, 05} \cdot I_{Z} \cdot G_{0, 05} \cdot I_{tor}}}{l_{ef}}

M_crit	Kritisches Biegemoment
E_0,05	5 % Quantile des Elastizitätsmoduls
G_0,05	5 % Quantile des Schubmoduls
I_z	Trägheitsmoment um die schwache Achse
I_T	Torsionsträgheitsmoment
l_ef	Ersatzstablänge

Критический изгибающий момент

M_crit = 18 482,84 кНм

Ожидать можно было значение, аналогичное системе с жесткими промежуточными опорами. Как при потере устойчивости плоской формы изгиба в деревянных конструкциях | теории, то применение расширенной формулы с α и β ограничено.

Потеря устойчивости плоской формы изгиба в деревянных конструкциях | Способ расчёта

Строго говоря, формула действительна только в случае прогиба по большой синусоидальной дуге. Другими словами, если основание очень пластично. В нашем примере это не так. Многоволновые собственные функции, которые при более высоких константах упругости приводят к более низкой критической нагрузке, не включены в вышеупомянутое уравнение, поскольку оно основано на односоставном синусовом подходе.

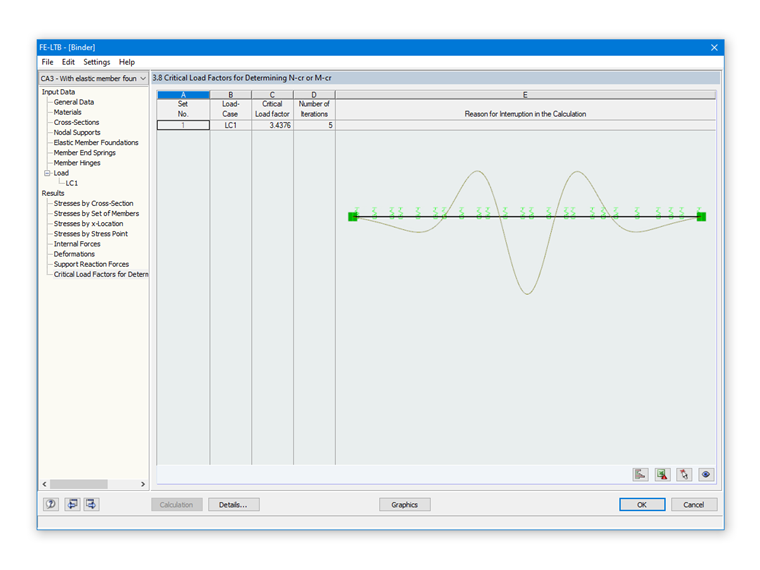
Как видно на рисунке 07, результатом анализа собственных значений является многоволновая собственная форма.

6 Результаты расчета методом собственных чисел у однопролетной балки с вильчатым опиранием и упругим основанием стержня

В данном случае можно применить метод, разработанный профессором Генрихом Кройцингером (2020). Критический изгибающий момент рассчитывается следующим образом:

M_{crit} = \frac{(2 \cdot e \cdot c^{*} - a_{z}^{*} \cdot B^{*}) + \sqrt{{(2 \cdot e \cdot c^{*} - a_{z}^{*} \cdot B^{*})}^{2} + 4 \cdot 1, 0 \cdot (B^{*} \cdot T^{*} - e^{*} \cdot {c^{*}}^{2})}}{2}

c^{*} = K_{y} \cdot \frac{L^{2}}{π^{2} \cdot n^{2}}

a_{z}^{*} = \frac{a_{z}}{n^{2}}

B^{*} = E_{0, 05} \cdot I_{Z} \cdot \frac{π^{2} \cdot n^{2}}{L^{2}} + c^{*}

T^{*} = G_{0, 05} \cdot I_{T} + c^{*} \cdot e^{2}

n = 1, 2, 3 . . .

M_crit	Kritisches Biegemoment
a_z	Abstand des Lastangriffs vom Schubmittelpunkt
e	Abstand der Stabbettung vom Schubmittelpunkt
K_y	elastische Stabbettung pro Binder
L	Trägerlänge
n	n-te Eigenlösung
E_0,05	5 % Quantile des Elastizitätsmoduls
I_z	Trägheitsmoment um die schwache Achse
G_0,05	5 %-Quantile des Schubmoduls
I_T	Torsionsträgheitsmoment

Критический изгибающий момент

Константа n обозначает первое, второе, третье и т.д. собственное решение. Таким образом, необходимо проанализировать несколько собственных решений, а определяющим будет наименьший критический изгибающий момент. Следующие критические изгибающие моменты мы получим для n = 1…30.

n	M_crit [кНм]	n	M_crit[кНм]
1	9 523,25	16	2 214,63
2	4 281,26	17	2 339,17
3	2 294,32	18	2 464,92
4	1 605,56	19	2 591,63
5	1 354,68	20	2 719,14
6	1 282,70	21	2 847,30
7	1 294,12	22	2 976,00
8	1 348,81	23	3 105,16
9	1 428,05	24	3 234,71
10	1 522,29	25	3 364,60
11	1 626,24	26	3 494,77
12	1 736,77	27	3 625,20
13	1 851,94	28	3 755,84
14	1 970,50	29	3 886,67
15	2 091,60	30	4 017,68

При n = 6 M_crit имеет минимальное значение, которое равно 1 282,70 кНм.

Результатом решения собственных чисел в дополнительном модуле RF-/FE-LTB (см. Рисунок 07) является:

M_crit = 3,4376 ⋅ 405 кНм = 1 397,25 кНм

Оба результата практически совпадают. Кроме того, аналитическое решение является надежным, поскольку данный метод упрощенно основывается на постоянном распределении изгибающего момента. Постоянному критическому изгибающему моменту М_crit таким образом присваивается критическая нагрузка q_crit.

q_{crit} = \frac{M_{crit} \cdot 8}{L^{2}}

q_crit	Kritische Last
M_crit	Kritisches Biegemoment
L	Trägerlänge

Критическая нагрузка

Поскольку в данном примере основание стержня считается очень жестким и постоянным по всей длине фермы, то мы получим критические изгибающие моменты, которые немного выше, чем в случае жестких точечных опор.

Согласно [3], раздел 9.2.5.3 (2), жесткие связи должны обладать достаточной жесткостью для того, чтобы не был превышен горизонтальный прогиб L/500. Расчет должен выполняться с расчетными значениями жесткости (см. [1] Глава NCI по 9.2.5.3).

При k_crit = 0,195, H = 5 м и q_p = 0,65 кН/м² в качестве динамического давления порыва ветра мы получим следующие нагрузки (см. [3] раздел 9.2.5.3):

N_{d} = (1 - k_{crit}) \cdot \frac{M_{d}}{h}

N_d	Stabilisierungskraft für den Druckgurt
k_crit	Kippbeiwert
M_d	Bemessungsmoment
h	Trägerhöhe

Стабилизирующая сила для сжатого пояса

N_d = (1 - 0,195) ⋅ 405 / 1,2 = 271,68 кН

q_{d} = \sqrt{\frac{15}{L}} \cdot \frac{n \cdot N_{d}}{k_{f, 3} \cdot L}

q_d	Aussteifungslast
n	Anzahl der Binder
L	Trägerlänge
k_f,3	Modifikationsbeiwert für den Aussteifungswiderstand

Нагрузка на крепь

q_d = 2,76 кН/м

q_{d, Wind} = γ_{Q} \cdot (c_{pe, D} \cdot c_{pe, E}) \cdot q_{p} \cdot \frac{H}{2}

q_d,Wind	Bemessungslast aus Wind
γ_Q	Teilsicherheitsbeiwert für veränderliche Einwirkung
c_pe	Außendruckbeiwert
q_p	Böengeschwindigkeitsdruck
h	Höhe des Gebäudes

Расчетная ветровая нагрузка

q_d,ветер = 1,5 ⋅ (0,7 + 0,3) ⋅ 0,65 ⋅ 5 / 2 = 2,44 кН/м

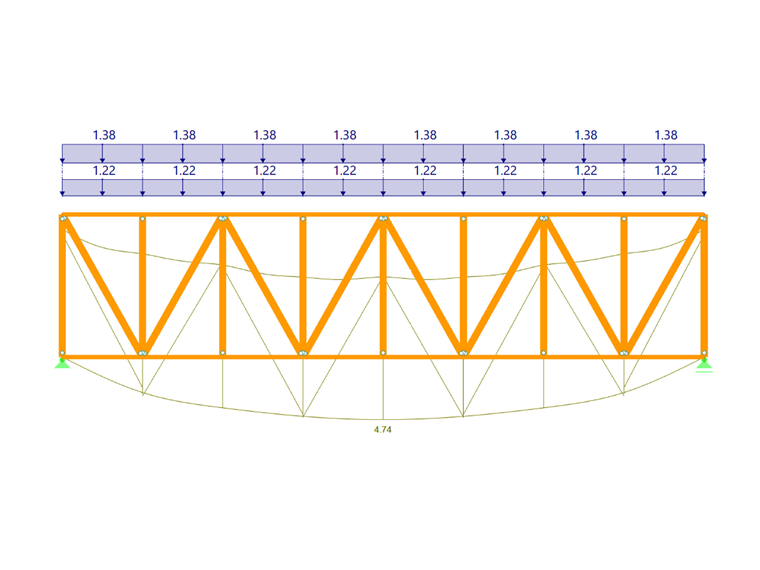
Деформация связей жесткости показана на рисунке 08. При этом нагрузки были снова разделены пополам из-за наличия двух связей жесткости.

Горизонтальное перемещение связей жесткости

Допустимая деформация составляет:

\frac{L}{500} = \frac{18 m}{500} = 36, 00 mm \geq 4, 74 mm

Допустимая деформация

Результат подтверждает предположение связи с высокой жесткостью и соответствует почти одинаковым критическим изгибающим моментам конструкции с жесткими промежуточными опорами и конструкции с упругим основанием стержня.

Заключение

В статье было показано, какие возможности существуют для расчета бокового выпучивания изогнутых балок в деревянных конструкциях. В применении распространенных методов решения важно обеспечить достаточную жесткость связей для того, чтобы можно было применить в расчете жесткие опоры. В нашей статье также были показаны варианты для тех случаев, когда данное предположение не действительно. Как правило, для изгибаемых балок и связей жесткости должен быть выполнен расчет несущей способности и пригодности к эксплуатации по соответствующей норме. Однако это не является предметом нашей статьи.

База знаний

KB 001669 | Потеря устойчивости плоской формы изгиба в деревянных конструкциях | Примеры 2

Автор

Г-н Рем отвечает за разработку продуктов для деревянных конструкций и оказывает техническую поддержку заказчикам.

Ссылки

DIN. (2013). Национальное приложение – Еврокод 5: Проектирование деревянных конструкций - Часть 1‑1: Allgemeines - Allgemeine Regeln und Regeln für den Hochbau; DIN EN 1995-1-1/NA:2013-08
Petersen, C.: (1982). Statik und Stabilität der Baukonstruktionen, (2-я издание. Висбаден: Vieweg, 1982
Еврокод 5: Проектирование деревянных конструкций - Часть 1‑1: Общее - Общие правила и правила для надземных сооружений; DIN EN 1995‑1‑1:2010‑12

;