返回知识库

6146x

001669

Dipl.-Ing.格哈德·雷姆（FH）

2020-12-18

木结构弯扭屈曲 | 示例 2

木结构中的弯扭屈曲位于上一个文章 | 示例 1 通过简单的示例说明了计算梁弯扭屈曲的临界弯矩 M_crit或临界弯曲应力 σ_crit的实际应用。此处临界弯矩是通过考虑由加劲支撑形成的弹性地基来计算的。

结构模型

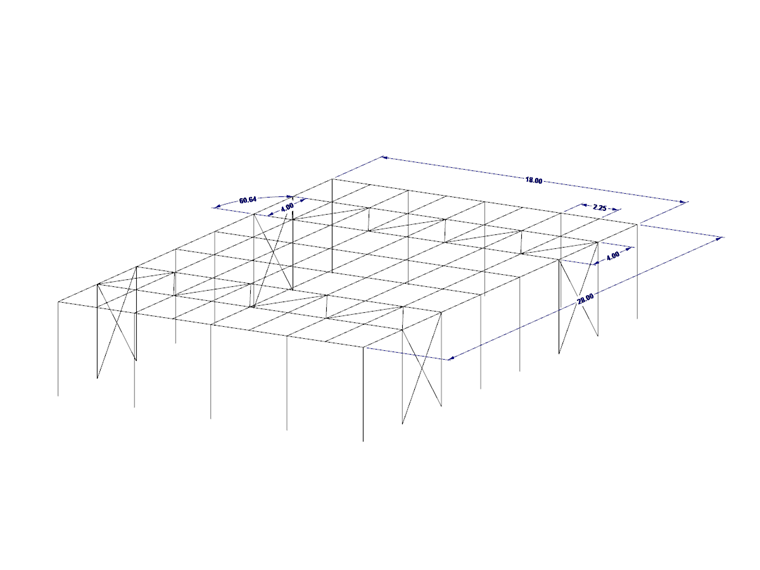
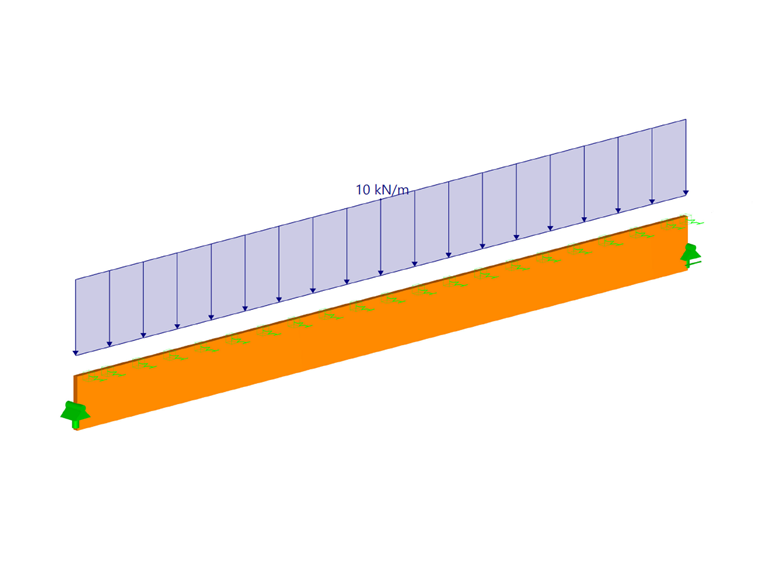
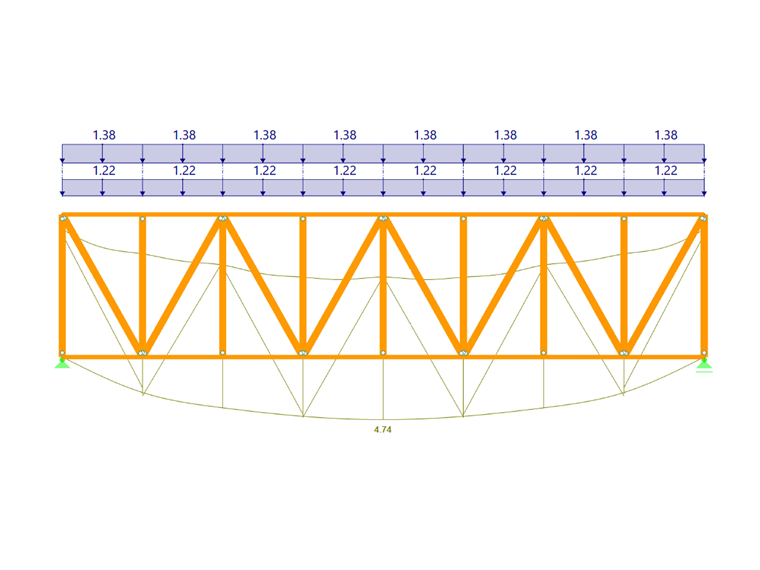
图01中的结构体系需要分析桁架的屈曲问题。屋顶平面上有 6 个长 18 m 的桁架平行梁和 2 个支撑。山墙上的梁由柱子支撑，在计算中不考虑。对桁架杆件施加 10 kN/m 的设计荷载 q_d 。

1 结构模型

模型数据

l	18	m	梁长度
B	120	mm	梁宽
h	1,200	mm	梁高
GL24h	-	-	材料按照 EN 14080
I_z	172.800.000	mm⁴	惯性矩
I_T	647.654.753	mm⁴	抗扭惯性矩
q_d	10	kN/m	荷载计算值
a_z	600	mm	荷载位置
e	600	mm	基础位置

请注意：以下用于 E 和 G 的公式虽然没有明确涉及系数中的 5% 分位数，但已被相应地考虑在内。

单跨无中间支座弯扭约束梁

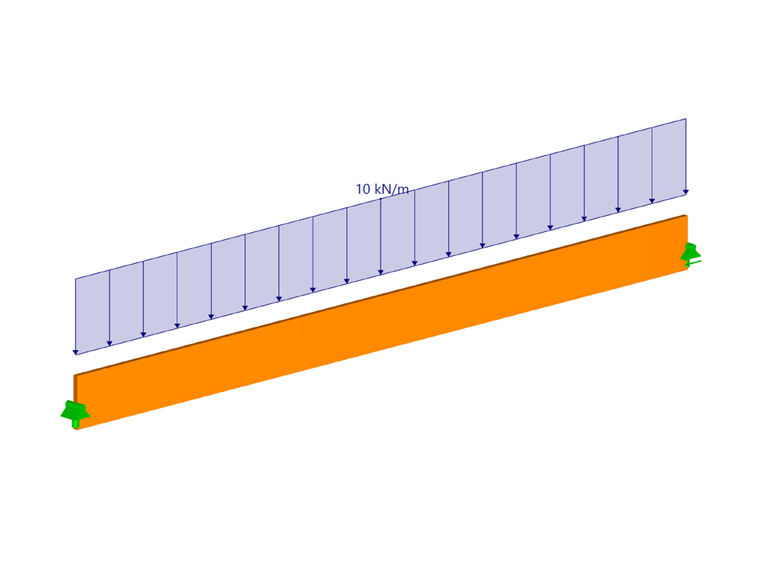
2 无侧向和扭转约束的单跨梁

为了完整起见，首先分析桁架，没有设置侧向支座（见图 02）。等效杆件长度是在桁架结构上部施加荷载时得出的，其中 a₁ = 1.13 和 a₂ = 1.44：

l_{ef} = \frac{L}{a_{1} \cdot (1 - a_{2} \cdot \frac{a_{z}}{L} \cdot \sqrt{\frac{E_{0, 05} \cdot I_{Z}}{G_{0, 05} \cdot I_{T}}})}

l_ef	Ersatzstablänge
L	Trägerlänge, Abstand der seitlichen Halterung
a₁,a₂	Kippbeiwerte
a_z	Abstand des Lastangriffs vom Schubmittelpunkt
E_0,05	5 % Quantile des Elastizitätsmoduls
G_0,05	5 % Quantile des Schubmoduls
I_z	Trägheitsmoment um die schwache Achse
I_T	Torsionsträgheitsmoment

等效杆件长度

l_ef = 17.79 m

临界弯矩可以按照下式计算：

M_{crit} = \frac{π \cdot \sqrt{E_{0, 05} \cdot I_{Z} \cdot G_{0, 05} \cdot I_{tor}}}{l_{ef}}

M_crit	Kritisches Biegemoment
E_0,05	5 % Quantile des Elastizitätsmoduls
G_0,05	5 % Quantile des Schubmoduls
I_z	Trägheitsmoment um die schwache Achse
I_T	Torsionsträgheitsmoment
l_ef	Ersatzstablänge

临界弯矩

M 临界 =_134.52 kNm

这些示例没有由于对层板胶合木梁的均匀化处理而导致刚度属性的 5% 分位数的增加。

桁架弯矩按照下式计算：

M_{d} = \frac{q_{d} \cdot L^{2}}{8}

M_d	Bemessungsmoment
q_d	Bemessungslast
L	Trägerlänge

设计弯矩

M_d = 405.00 kNm

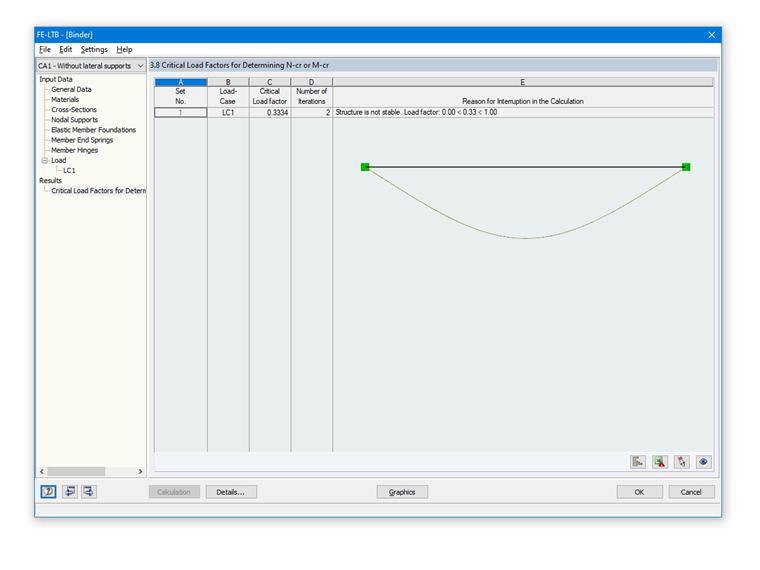
使用附加模块RF-/FE-LTB进行特征值分析时，其临界屈曲荷载系数为0.3334。由此可以得出，临界弯矩

M 临界 =_0.3334 ⋅ 405 kNm = 135.03 kNm

，因此与解析解的结果相同。

3 Ergebnis der Eigenwertanalyse für den gabelgelagerter Einfeldträger ohne Zwischenabstützungen

正如对于这个无支撑的细长桁架杆件一样，作用的弯矩大于临界弯矩（3 倍），因此桁架没有得到足够的约束以防止侧向屈曲。现在在计算中应该考虑一个支撑。

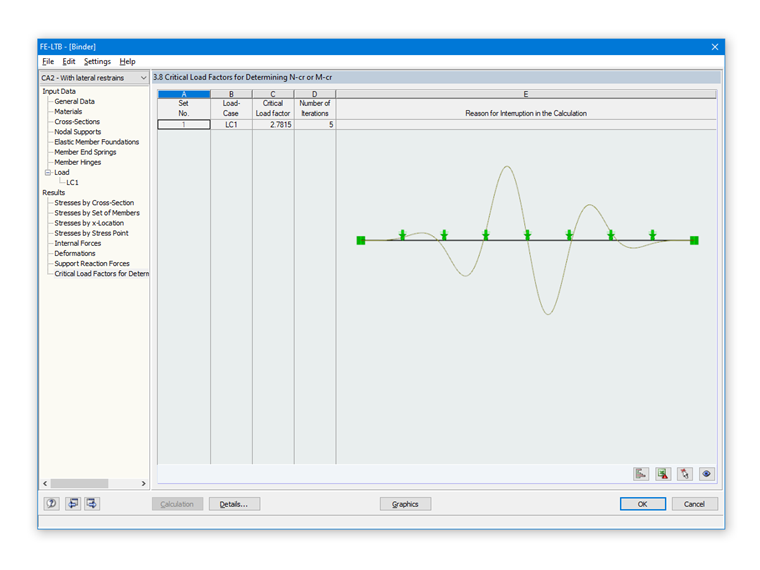
刚性约束弯扭的简支梁

4 刚性和中间扭转约束的单跨梁

如果横向屈曲支撑足够大，则侧向支座之间的间距（例如檩条）通常作为等效杆件长度进行侧向屈曲分析。在上一篇文章木结构中的侧向屈曲分析中已经介绍了这个方法。 | 示例 1.

木结构弯扭屈曲 | Beispiele 1

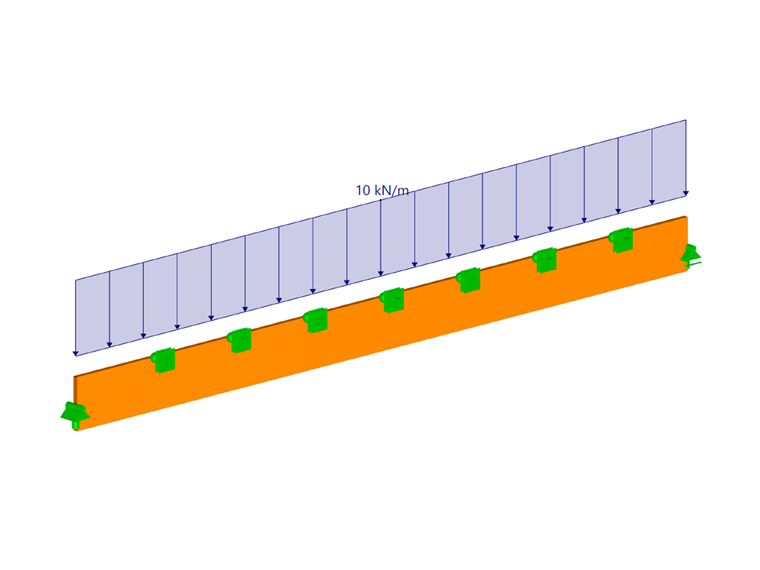
因此L取2.25 m。当 a₁ = 1.00 和 a₂ = 0.00 时，

l_{ef} = \frac{L}{a_{1} \cdot (1 - a_{2} \cdot \frac{a_{z}}{L} \cdot \sqrt{\frac{E_{0, 05} \cdot I_{z}}{G_{0, 05} \cdot I_{T}}})}

l_ef	Ersatzstablänge
L	Trägerlänge, Abstand der seitlichen Halterung
a₁,a₂	Kippbeiwerte
a_z	Abstand des Lastangriffs vom Schubmittelpunkt
E_0,05	5 % Quantile des Elastizitätsmoduls
G_0,05	5 % Quantile des Schubmoduls
I_z	Trägheitsmoment um die schwache Achse
I_T	Torsionsträgheitsmoment

等效杆件长度

l_ef = 2,25 m

临界弯矩值的计算结果如下：

M_{crit} = \frac{π \cdot \sqrt{E_{0, 05} \cdot I_{Z} \cdot G_{0, 05} \cdot I_{tor}}}{l_{ef}}

M_crit	Kritisches Biegemoment
E_0,05	5 % Quantile des Elastizitätsmoduls
G_0,05	5 % Quantile des Schubmoduls
I_z	Trägheitsmoment um die schwache Achse
I_T	Torsionsträgheitsmoment
l_ef	Ersatzstablänge

临界弯矩

M 临界 =_1063.51 kNm

因为作用在梁上的弯矩小于临界弯矩，所以在刚性中间支座假设情况下，梁不会出现侧向屈曲。

使用附加模块 RF-/FE-LTB 进行特征值分析的结果是，该项目的临界屈曲荷载系数为 2.7815。由此可以得出，临界弯矩

M_{crit} = η \cdot M_{d}

M_crit	Kritisches Biegemoment
η	Verzweigungslastfaktor
M_d	Bemessungsmoment

临界弯矩

M 临界 =_2.7815 ⋅ 405 kNm = 1.126.50 kNm

5 Ergebnis der Eigenwertanalyse für den gabelgelagerten Einfeldträger mit starren Zwischenabstützungen

考虑弯扭约束的单跨梁和杆件弹性地基

具有跨度和扭转约束的单跨梁和杆件弹性地基

与木结构中的弯扭屈曲相关 | ，对于 55% 弹性地基，在确定等效杆件长度的基础上扩大了系数 α 和 β，请参阅 [1]]] 弹性地基。

木结构弯扭屈曲 | 验算方法

这样可以考虑桁架杆件侧向屈曲的加劲支撑的剪切刚度. 支撑的抗剪刚度可以例如按照{%于#Refer [2]]] 图 6.34 确定。从上文可以看出，它取决于支撑的类型、斜腹杆和支撑杆的应变刚度、斜腹杆的倾角以及紧固件的延性。如图01所示，剪切刚度为：

s_{id} = E_{D} \cdot A_{D} \cdot \sin {(α)}^{2} \cdot \cos (α)

s_id	Ideelle Schubsteifigkeit des Aussteifungsverbandes
E_D	5 % Quantile des Elastizitätsmoduls der Diagonalen
A_D	Querschnittsfläche der Diagonalen
α	Winkel zwischen der Diagonalen und der Gurte

加固支座的理想抗剪刚度

式中 E_D是'对角线弹性模量，截面积 A_D 。但是，上面的公式不包括对角线 ' 紧固件的延性。这以及对角线的杆件伸长可以通过名义截面面积 A_D '来考虑。以下是说明：

s_{id} = E_{D} \cdot A_{D}' \cdot \sin {(α)}^{2} \cdot \cos (α)

s_id	Ideelle Schubsteifigkeit des Aussteifungsverbandes
E_D	5 % Quantile des Elastizitätsmoduls der Diagonalen
A_D'	Fiktive Querschnittsfläche der Diagonalen
α	Winkel zwischen der Diagonalen und der Gurte

加固支座的理想抗剪刚度

值:

A_{D}' = \frac{A_{D}}{1 + \frac{E_{D} \cdot A_{D}}{L_{D}} \cdot \sum \frac{1}{K_{ser}}}

A_D'	Fiktive Querschnittsfläche der Diagonalen
A_D	Querschnittsfläche der Diagonalen
E_D	5 % Quantile des Elastizitätsmoduls der Diagonalen
L_D	Länge der Diagonalen
K_ser	Verschiebungsmodul der Verbindung

对角线名义截面面积

斜杆的尺寸为宽/高 = 120/200 mm，长度 L_D为 4.59 m。在对角线每侧的连接的滑移模量应为 110000 N/mm。

则理想面积是

A_D ' = 12548 mm²

斜杆与弦的夹角为 60.64 °，支撑的抗剪刚度为

s_{id} = E_{D} \cdot A_{D}' \cdot \sin {(α)}^{2} \cdot \cos (α)

s_id	Ideelle Schubsteifigkeit des Aussteifungsverbandes
E_D	5 % Quantile des Elastizitätsmoduls der Diagonalen
A_D'	Fiktive Querschnittsfläche der Diagonalen
α	Winkel zwischen der Diagonalen und der Gurte

加固支座的理想抗剪刚度

s_id = 44 864 kN

单个支撑的杆件基础中的长度可根据 [2] 公式 7.291 进行转换：

K_{y}' = s_{id} \cdot \frac{π^{2}}{L^{2}}

K_{y}' = 44.864 kN \cdot \frac{π^{2}}{{(18 m)}^{2}} = 1.367 \frac{kN}{m^{2}} = 1, 367 \frac{N}{{mm}^{2}}

K_y'	Elastische Stabbettung pro Verband
s_id	Ideelle Schubsteifigkeit des Aussteifungsverbandes
L	Länge des Verbandes

弹性杆件基础每个支撑

对于两个支撑和六个杆件，每个杆件的弹簧常数如下：

K_{y} = \frac{2 \cdot K_{y}'}{6}

K_y	Elastische Stabbettung pro Binder
K_y'	Elastische Stabbettung pro Verband

每个桁架杆件的弹性杆件基础

K_y = 455,6 kN/m² = 0.456 N/mm²

K_G = ∞、K_θ = 0、K_y = 0.456 N/mm²、e = 600 mm、a₁ = 1.13 和 a₂ = 1.44，得出等效的杆件长度为：

l_{ef} = \frac{L}{a_{1} \cdot (1 - a_{2} \cdot \frac{a_{z}}{L} \cdot \sqrt{\frac{E_{0, 05} \cdot I_{z}}{G_{0, 05} \cdot I_{T}}})} \cdot \frac{1}{α \cdot β}

l_ef	Ersatzstablänge
L	Trägerlänge, Abstand der seitlichen Halterung
a₁,a₂	Kippbeiwerte
a_z	Abstand des Lastangriffs vom Schubmittelpunkt
E_0,05	5 % Quantile des Elastizitätsmoduls
G_0,05	5 % Quantile des Schubmoduls
I_z	Trägheitsmoment um die schwache Achse
I_T	Torsionsträgheitsmoment
α, β	Beiwerte zur Berücksichtigung einer Stabbettung

等效杆件长度

l_ef = 0.13

因此，临界弯矩为一个不切实际的值：

M_{crit} = \frac{π \cdot \sqrt{E_{0, 05} \cdot I_{Z} \cdot G_{0, 05} \cdot I_{tor}}}{l_{ef}}

M_crit	Kritisches Biegemoment
E_0,05	5 % Quantile des Elastizitätsmoduls
G_0,05	5 % Quantile des Schubmoduls
I_z	Trägheitsmoment um die schwache Achse
I_T	Torsionsträgheitsmoment
l_ef	Ersatzstablänge

临界弯矩

M 临界 =_18482.84 kNm

该值类似于具有刚性中间支座的结构体系。与木结构中的弯扭屈曲相关 | 理论上，带 α 和 β 的扩展公式的应用受到限制。

木结构弯扭屈曲 | 验算方法

严格来说，该选项只有在挠度呈正弦大弧形时才有效。也就是说，如果地基非常松软。本例中不再给出。由于上面的公式是基于单项式正弦函数法的，所以上面的公式中不包含多次波的特征函数，在任意较大的弹簧常数下导致小的临界屈曲荷载。

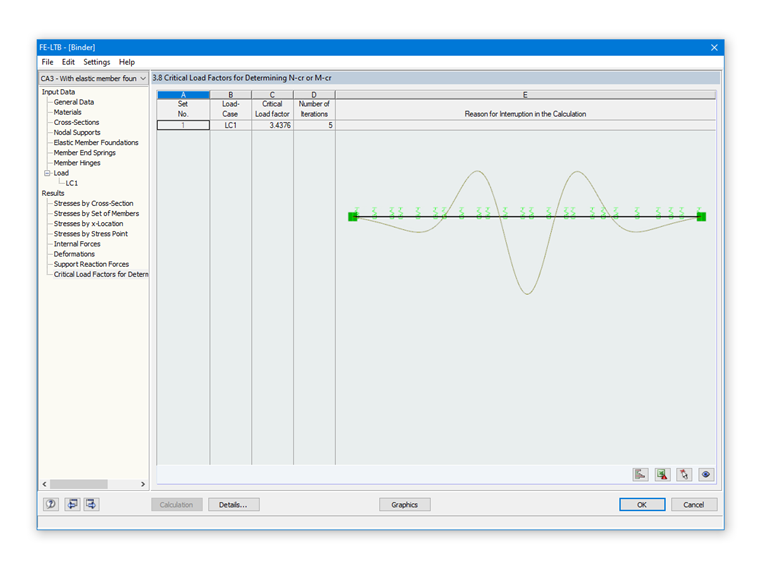
正如图 07 所看到的，由特征值分析得出的多波特征向量。

6 Ergebnis der Eigenwertanalyse für den gabelgelagerten Einfeldträger mit elastischer Stabbettung

在这种情况下，可以应用 Heinrich Kreuzinger 博士 Prof. (2020) 的方法。临界弯矩计算如下：

M_{crit} = \frac{(2 \cdot e \cdot c^{*} - a_{z}^{*} \cdot B^{*}) + \sqrt{{(2 \cdot e \cdot c^{*} - a_{z}^{*} \cdot B^{*})}^{2} + 4 \cdot 1, 0 \cdot (B^{*} \cdot T^{*} - e^{*} \cdot {c^{*}}^{2})}}{2}

c^{*} = K_{y} \cdot \frac{L^{2}}{π^{2} \cdot n^{2}}

a_{z}^{*} = \frac{a_{z}}{n^{2}}

B^{*} = E_{0, 05} \cdot I_{Z} \cdot \frac{π^{2} \cdot n^{2}}{L^{2}} + c^{*}

T^{*} = G_{0, 05} \cdot I_{T} + c^{*} \cdot e^{2}

n = 1, 2, 3 . . .

M_crit	Kritisches Biegemoment
a_z	Abstand des Lastangriffs vom Schubmittelpunkt
e	Abstand der Stabbettung vom Schubmittelpunkt
K_y	elastische Stabbettung pro Binder
L	Trägerlänge
n	n-te Eigenlösung
E_0,05	5 % Quantile des Elastizitätsmoduls
I_z	Trägheitsmoment um die schwache Achse
G_0,05	5 %-Quantile des Schubmoduls
I_T	Torsionsträgheitsmoment

临界弯矩

常数 n 表示第一、第二、第三等振型解。因此，必须要分析几个特征值解，最小的临界弯矩值将起到决定性的作用。以下是当 n = 1…30 时的临界弯矩值。

n	M_临界 [kNm]	n	M_临界[kNm]
1	9.523,25	16	2.214,63
2	4.281,26	17	2.339,17
3	2.294,32	18	2.464,92
4	1.605,56	19	2.591,63
5	1.354,68	20	2.719,14
6	1.282,70	21	2.847,30
7	1.294,12	22	2.976,00
8	1.348,81	23	3.105,16
9	1.428,05	24	3.234,71
10	1.522,29	25	3.364,60
11	1.626,24	26	3.494,77
12	1.736,77	27	3.625,20
13	1.851,94	28	3.755,84
14	1.970,50	29	3.886,67
15	2.091,60	30	4.017,68

M 临界在 n = 6 时最小，约为_1282.70 kNm。

根据附加模块 RF-/FE-LTB 的特征值解（见图 07）为：

M 临界 =_3.4376 ⋅ 405 kNm = 1.397.25 kNm

两个结果一致。然而，解析解是安全的，因为该方法是基于恒定弯矩分布的。然后对恒定临界弯矩M_crit分配临界荷载qcrit 。

q_{crit} = \frac{M_{crit} \cdot 8}{L^{2}}

q_crit	Kritische Last
M_crit	Kritisches Biegemoment
L	Trägerlänge

临界荷载

因为这个例子中的杆件基础被认为是非常刚的并且恒定分布在桁架杆件长度上，所以产生的临界弯矩略大于刚性的单个支座下的弯矩。

根据 {%于#参见[3]]] 章节 9.2.5.3 (2) ，加劲支撑的刚度必须不超过水平挠度 L/500。必须使用刚度的设计值进行计算（见 [1] 章节 NCI 到 9.2.5.3）。

当 k_crit = 0.195，H = 5 m 且阵风速度压力 q_p = 0.65 kN/m² 时，得出以下荷载（见 {%间#Refer [3]]] 章节 9.2.5.3）：

N_{d} = (1 - k_{crit}) \cdot \frac{M_{d}}{h}

N_d	Stabilisierungskraft für den Druckgurt
k_crit	Kippbeiwert
M_d	Bemessungsmoment
h	Trägerhöhe

压缩弦的稳定力

N_d = (1 - 0,195) ⋅ 405/1,2 = 271,68 kN

q_{d} = \sqrt{\frac{15}{L}} \cdot \frac{n \cdot N_{d}}{k_{f, 3} \cdot L}

q_d	Aussteifungslast
n	Anzahl der Binder
L	Trägerlänge
k_f,3	Modifikationsbeiwert für den Aussteifungswiderstand

加劲荷载

q_d = 2.76 kN/m

q_{d, Wind} = γ_{Q} \cdot (c_{pe, D} \cdot c_{pe, E}) \cdot q_{p} \cdot \frac{H}{2}

q_d,Wind	Bemessungslast aus Wind
γ_Q	Teilsicherheitsbeiwert für veränderliche Einwirkung
c_pe	Außendruckbeiwert
q_p	Böengeschwindigkeitsdruck
h	Höhe des Gebäudes

风荷载

q_d,wind = 1.5 ⋅ (0.7 + 0.3) ⋅ 0.65 ⋅ 5/2 = 2.44 kN/m

加劲支撑的变形如图08所示。因为有两个加劲支撑，所以荷载分成两半。

加固支撑的水平位移

容许变形为：

\frac{L}{500} = \frac{18 m}{500} = 36, 00 mm \geq 4, 74 mm

容许变形

结果验证了系统为非常刚度的支撑的假设，并且在刚性中间支座和弹性支座的系统中有着几乎相同的临界弯矩。

概述总结

展示了在木结构中的哪些可能性可以用于分析受弯梁的侧向屈曲。通常的计算方法都需要注意，支撑结构必须具有足够的刚度，以便能够承受刚性支座。本文列出了不适用这种假设的情况。原则上对弯梁和加劲支撑必须按照相应的规范进行承载力和正常使用设计。这不属于本文的讨论范围。

知识库

KB 001669 | 木结构翘曲屈曲 | 示例2

作者

Rehm 先生负责木结构产品的开发，并提供技术支持。

链接

参考

国家附录 - 欧洲规范 5：木结构设计 - 第1-1部分：总则 - 通用规范和建筑规范； DIN EN 1995‑1‑1/NA:2013‑08
Petersen, C. (1982). Statik und Stabilität der Baukonstruktionen , (2nd 编）。威斯巴登：视图eg。
欧洲规范 5：木结构设计 - 第1-1部分：总则 – 通用规范和建筑规范DIN EN 1995-1-1:2010-12

;