5701x

001669

Dipl.-Ing. (FH) Gerhard Rehm

2020-12-18

Lateral-Torsional Buckling in Timber Structures | Examples 2

The previous article Lateral-Torsional Buckling in Timber Construction | Examples 1 explains the practical application for determining the critical bending moment M_crit or the critical bending stress σcrit for a bending beam's lateral-torsional buckling by using simple examples. In this article, the critical bending moment is determined by considering an elastic foundation resulting from a stiffening bracing.

Structural Model

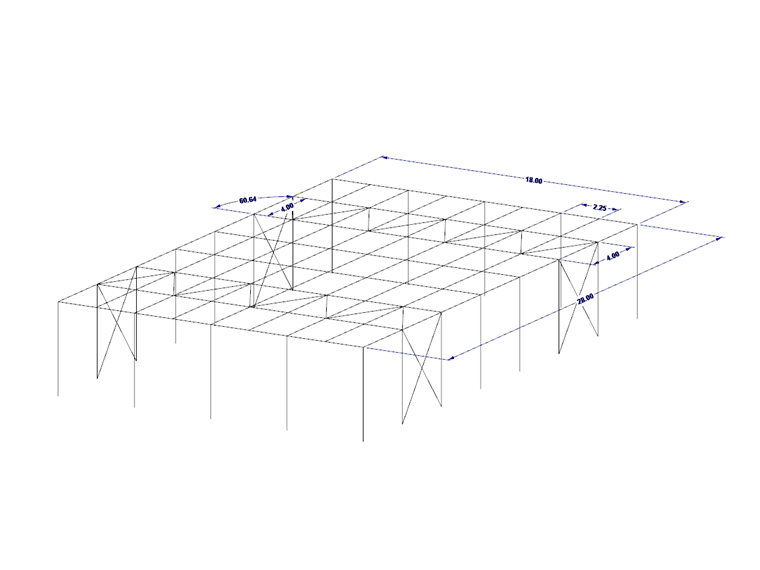
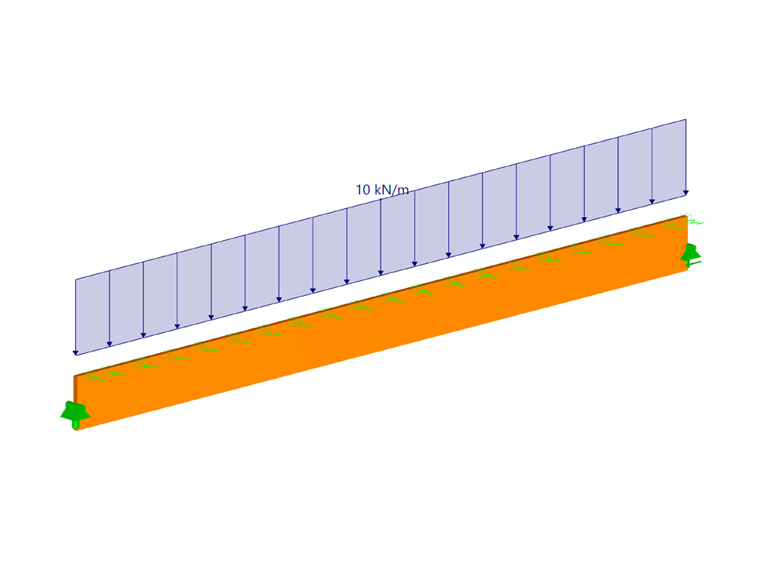
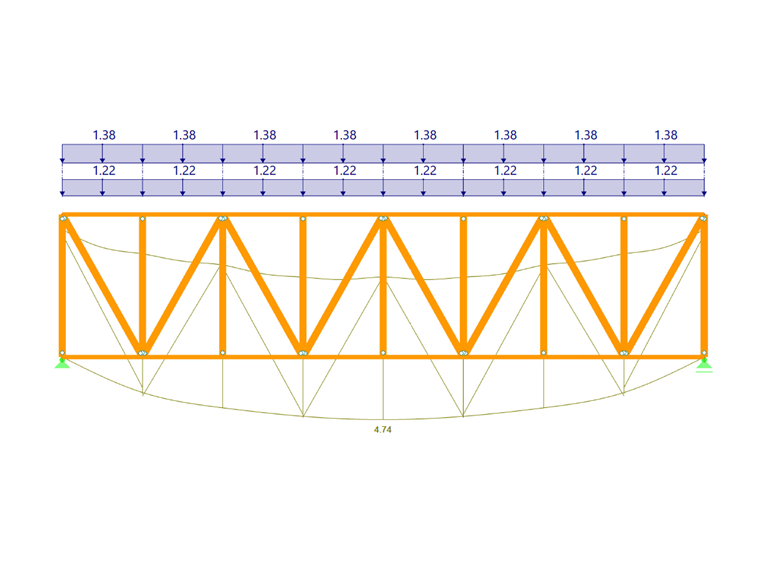
For the system shown in Image 01, the truss members should be analyzed for lateral buckling. In the roof plane, six truss members are available as parallel beams with a length of 18 m and two stiffening bracings. The beams on the gable sides are supported by columns and are not considered for the calculation. A design load q_d of 10 kN/m acts on the truss members.

1 Structural Model

Model Data

L	18	m	Beam length
b	120	mm	Beam width
h	1.200	mm	Beam height
GL24h	-	-	Material according to EN 14080
I_z	172.800.000	mm⁴	Moment of inertia
I_T	647.654.753	mm⁴	Torsion moment of inertia
q_d	10	kN/m	Design load
a_z	600	mm	Load position
e	600	mm	Foundation position

Note: Even if the following equations for E and G do not explicitly refer to the 5%-quantiles in the index, they have been taken into account accordingly.

Single-Span Beam with Lateral and Torsional Restraint Without Intermediate Supports

2 Single-Span Beam with Lateral and Torsional Restraint Without Intermediate Supports

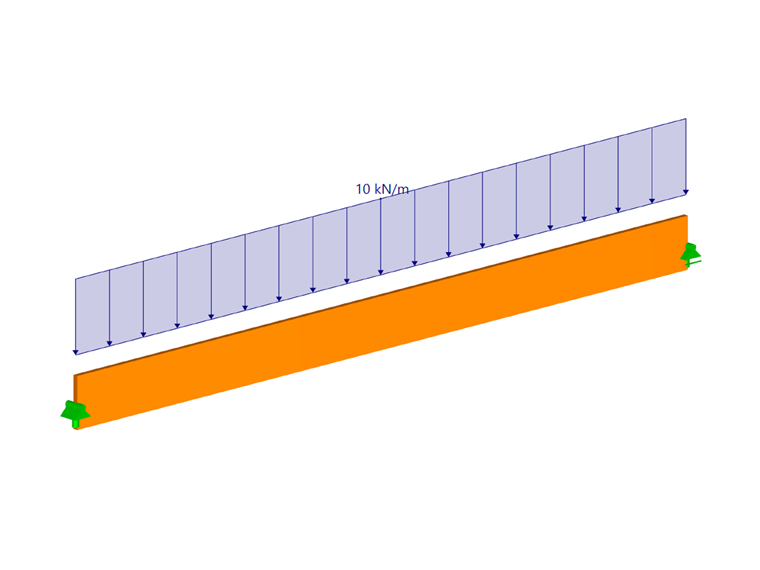
For the sake of completeness, the truss member is analyzed first, without lateral supports (see Image 02). The equivalent member length results from a load application on the upper side of the truss with a₁ = 1.13 and a₂ = 1.44 as follows:

l_{ef} = \frac{L}{a_{1} \cdot (1 - a_{2} \cdot \frac{a_{z}}{L} \cdot \sqrt{\frac{E_{0.05} \cdot I_{Z}}{G_{0.05} \cdot I_{T}}})}

l_ef	Equivalent member length
L	Beam length, spacing between lateral supports
a₁,a₂	Lateral buckling factors
a_z	Distance of load application from shear center
E_0.05	5 % quantile of modulus of elasticity
G_0.05	5 % quantile of shear modulus
I_z	Second moment of area about weak axis
I_T	Torsional constant

Equivalent Member Length

l_ef = 17.79 m

The critical bending moment can then be calculated as follows:

M_{crit} = \frac{π \cdot \sqrt{E_{0.05} \cdot I_{Z} \cdot G_{0.05} \cdot I_{tor}}}{l_{ef}}

M_crit	Critical bending moment
E_0.05	5 % quantile of modulus of elasticity
G_0.05	5 % quantile of shear modulus
I_z	Second moment of area about weak axis
I_T	Torsional constant
l_ef	Equivalent member length

Critical Bending Moment

M_crit = 134.52 kNm

These examples do without an increase of the product of the 5%-quantiles of the stiffness properties due to the homogenization of beams made of glued-laminated timber.

The bending moment acting on the trusses results as follows:

M_{d} = \frac{q_{d} \cdot L^{2}}{8}

M_d	Design moment
q_d	Design load
L	Beam length

Design Moment

M_d = 405.00 kNm

The eigenvalue analysis with the RF-/FE-LTB add-on module provides a critical buckling load factor of 0.3334 as a result. This results in the critical bending moment

M_crit = 0.3334 ⋅ 405 kNm = 135.03 kNm

and is thus identical to the result of the analytical solution.

3 Result of Eigenvalue Analysis for Single-Span Beam with Lateral and Torsional Restraint Without Intermediate Supports

As was to be expected for this unsupported, slender truss member, the acting bending moment is greater (by a factor of 3) than the critical bending moment, and the truss is thus not sufficiently restrained against lateral buckling. However, a bracing should counteract, which is now considered for the calculation.

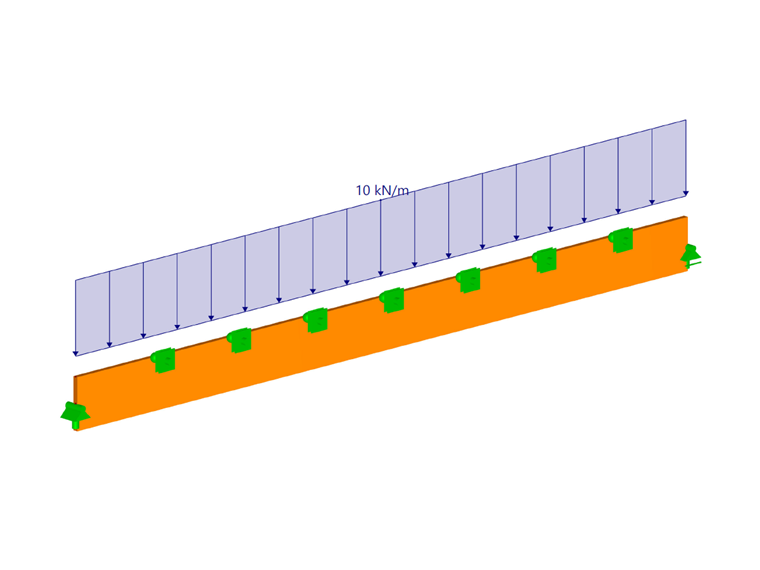
Single-Span Beam with Lateral and Torsional Restraint with Rigid Intermediate Supports

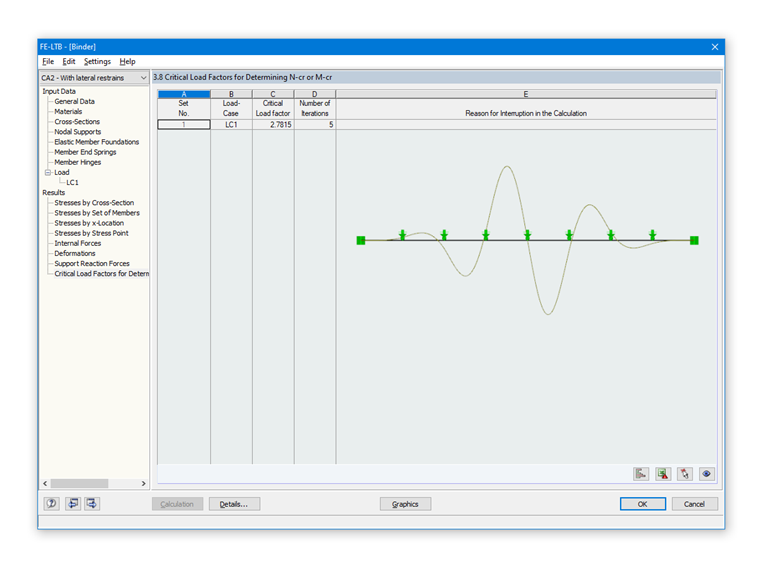
4 Single-Span Beam with Lateral and Torsional Restraint with Rigid Intermediate Supports

If the stiffening bracing is stiff enough, the spacing between the lateral supports (for example, by purlins) is often used as an equivalent member length for the lateral buckling analysis. This procedure was described in the previous article Lateral-Torsional Buckling in Timber Construction | Examples 1.

Lateral-Torsional Buckling in Timber Structures | Examples 1

Thus, 2.25 m is used as L. For a₁ = 1.00 and a₂ = 0.00, this follows:

l_{ef} = \frac{L}{a_{1} \cdot (1 - a_{2} \cdot \frac{a_{z}}{L} \cdot \sqrt{\frac{E_{0, 05} \cdot I_{z}}{G_{0, 05} \cdot I_{T}}})}

l_ef	Equivalent member length
L	Beam length, spacing between lateral supports
a₁,a₂	Lateral buckling factors
a_z	Load application distance from the shear center
E_0.05	5% quantile of the modulus of elasticity
G_0.05	5% quantile of the shear modulus
I_z	Second moment of area about the weak axis
I_T	Torsional constant

Equivalent Member Length

l_ef = 2.25 m

The following results for the critical bending moment:

M_{crit} = \frac{π \cdot \sqrt{E_{0.05} \cdot I_{Z} \cdot G_{0.05} \cdot I_{tor}}}{l_{ef}}

M_crit	Critical bending moment
E_0.05	5 % quantile of the modulus of elasticity
G_0.05	5 % quantile of the shear modulus
I_z	Second moment of the area about the weak axis
I_T	Torsional constant
l_ef	Equivalent member length

Critical Bending Moment

M_crit = 1,063.51 kNm

Since the bending moment acting on the beam is smaller than the critical bending moment, the beam is not endangered by lateral buckling under the assumption of rigid intermediate supports.

The eigenvalue analysis with the RF-/FE-LTB add-on module provides a critical buckling load factor of 2.7815 as a result. This results in the critical bending moment

M_{crit} = η \cdot M_{d}

M_crit	Critical bending moment
η	Critical buckling load factor
M_d	Design moment

Critical Bending Moment

M_crit = 2.7815 ⋅ 405 kNm = 1,126.50 kNm

5 Result of Eigenvalue Analysis for Single-Span Beam with Lateral and Torsional Restraint with Rigid Intermediate Supports

Single-Span Beam with Lateral and Torsional Restraint and Member Elastic Foundation

As described in Lateral-Torsional Buckling in Timber Construction | Theory, the determination of the equivalent member length for members on elastic foundation is extended by the factors α and β in [1].

Lateral-Torsional Buckling in Timber Structures | Theory

Thus, it is possible to consider the shear stiffness of a stiffening bracing for the lateral buckling of the truss members. The bracing's shear stiffness can be determined, for example, according to [2], Figure 6.34. As can be seen from the above, it depends on the type of bracing, the strain stiffness of diagonals and posts, the diagonals' inclination, and the ductility of the fasteners. For the stiffening bracing shown in Image 01, the shear stiffness results in:

s_{id} = E_{D} \cdot A_{D} \cdot \sin {(α)}^{2} \cdot \cos (α)

s_id	Ideal shear stiffness of the stiffening bracing
E_D	5 % quantile of the diagonals' modulus of elasticity
A_D	Cross-sectional area of diagonals
α	Angle between diagonals and chords

Ideal Shear Stiffness of Stiffening Bracing

Here, E_D is the diagonals' modulus of elasticity and A_D is their cross-sectional area. However, the equation above does not include the ductility of the diagonals' fasteners. This and the member elongation of the diagonals can be considered by means of a notional cross-section area A_D'. What follows is this:

s_{id} = E_{D} \cdot A_{D}' \cdot \sin {(α)}^{2} \cdot \cos (α)

s_id	Ideal shear stiffness of the stiffening bracing
E_D	5 % quantile of the diagonals' modulus of elasticity
A_D'	Notional cross-sectional area of diagonals
α	Angle between diagonals and chords

Ideal Shear Stiffness of Stiffening Bracing

where

A_{D}' = \frac{A_{D}}{1 + \frac{E_{D} \cdot A_{D}}{L_{D}} \cdot \sum \frac{1}{K_{ser}}}

A_D'	Notional cross-sectional area of diagonals
A_D	Cross-sectional area of diagonals
E_D	5 % quantile of the diagonals' modulus of elasticity
L_D	Length of diagonals
K_ser	Slip modulus of the connection

Notional Cross-Sectional Area of Diagonals

The diagonals have a dimension of w/h = 120/200 mm and a length L_D of 4.59 m. The slip modulus of the connection on each side of the diagonals should be 110,000 N/mm.

The ideal area is, accordingly,

A_D' = 12,548 mm²

and thus, the shear stiffness of a bracing with a diagonals-to-chord angle of 60.64 ° is

s_{id} = E_{D} \cdot A_{D}' \cdot \sin {(α)}^{2} \cdot \cos (α)

s_id	Ideal shear stiffness of the stiffening bracing
E_D	5 % quantile of the diagonals' modulus of elasticity
A_D'	Notional cross-sectional area of diagonals
α	Angle between diagonals and chords

Ideal Shear Stiffness of Stiffening Bracing

s_id = 44,864 kN

The member foundation per bracing can be converted according to [2], Formula 7.291 as follows:

K_{y}' = s_{id} \cdot \frac{π^{2}}{L^{2}}

K_{y}' = 44, 864 kN \cdot \frac{π^{2}}{{(18 m)}^{2}} = 1, 367 \frac{kN}{m^{2}} = 1.367 \frac{N}{{mm}^{2}}

K_y'	Elastic member foundation per bracing
s_id	Ideal shear stiffness of the stiffening bracing
L	Bracing length

Elastic Member Foundation per Bracing

For two bracings and six truss members, the following spring constant is available per truss:

K_{y} = \frac{2 \cdot K_{y}'}{6}

K_y	Elastic member foundation per truss member
K_y'	Elastic member foundation per bracing

Elastic Member Foundation per Truss Member

K_y = 455.6 kN/m² = 0.456 N/mm²

Provided that K_G = ∞, K_θ = 0, K_y = 0.456 N/mm², e = 600 mm, a₁ = 1.13, and a₂ = 1.44, the equivalent member length results in:

l_{ef} = \frac{L}{a_{1} \cdot (1 - a_{2} \cdot \frac{a_{z}}{L} \cdot \sqrt{\frac{E_{0.05} \cdot I_{z}}{G_{0.05} \cdot I_{T}}})} \cdot \frac{1}{α \cdot β}

l_ef	Equivalent member length
L	Beam length, spacing between lateral supports
a₁,a₂	Lateral buckling factors
a_z	Distance of the load application from the shear center
E_0.05	5 % quantile of the modulus of elasticity
G_0.05	5 % quantile of shear modulus
I_z	Second moment of the area about the weak axis
I_T	Torsional constant
α, β	Factors for considering a member foundation

Equivalent Member Length

l_ef = 0.13

Thus, the critical bending moment results in an unrealistic value of:

M_{crit} = \frac{π \cdot \sqrt{E_{0.05} \cdot I_{Z} \cdot G_{0.05} \cdot I_{tor}}}{l_{ef}}

M_crit	Critical bending moment
E_0.05	5 % quantile of the modulus of elasticity
G_0.05	5 % quantile of the shear modulus
I_z	Second moment of the area about the weak axis
I_T	Torsional constant
l_ef	Equivalent member length

Critical Bending Moment

M_crit = 18,482.84 kNm

A value similar to the system with rigid intermediate supports would be expected. As described in Lateral-Torsional Buckling in Timber Construction | Theory, the application of the extended formula with α and β is limited in its application.

Lateral-Torsional Buckling in Timber Structures | Theory

Strictly speaking, it is only valid if there is a deflection in a large sinusoidal arc. In other words, if the foundation is very soft. This is no longer given in this example. Multi-wave eigenfunctions, leading to a small critical buckling load for any larger spring constant, are not included in the aforesaid equation, since it is based on monomial sinus approaches.

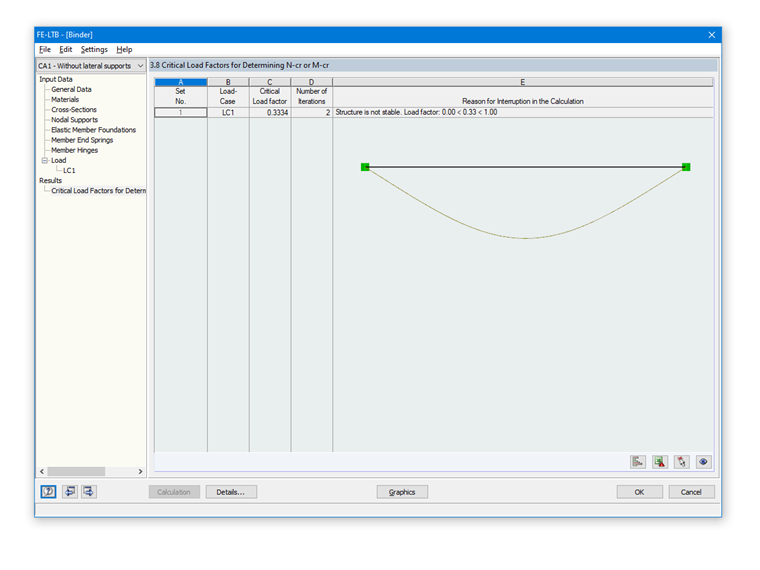
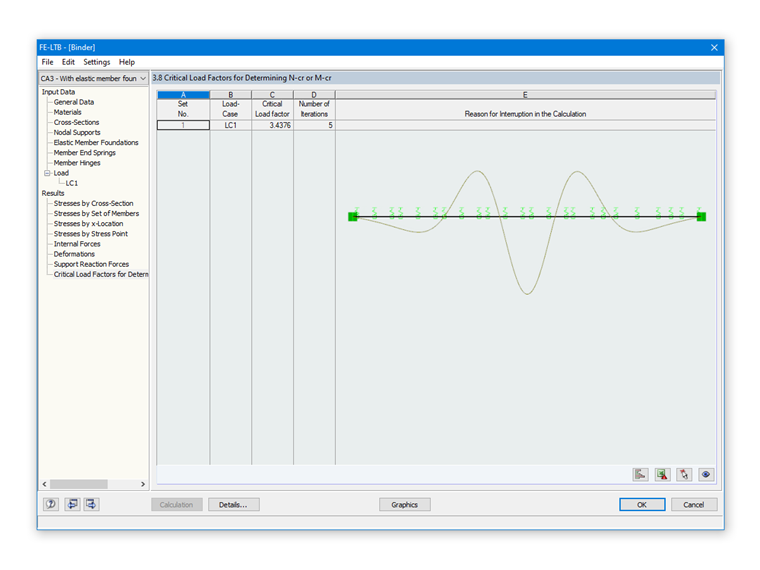
As you can see in Image 07, a multi-wave eigenvector results from the eigenvalue analysis.

6 Result of Eigenvalue Analysis for Single-Span Beam with Lateral and Torsional Restraint with Elastic Member Foundation

In this case, the method derived by Prof. Dr. Heinrich Kreuzinger (2020) can be applied. The critical bending moment is calculated as follows:

M_{crit} = \frac{(2 \cdot e \cdot c^{*} - a_{z}^{*} \cdot B^{*}) + \sqrt{{(2 \cdot e \cdot c^{*} - a_{z}^{*} \cdot B^{*})}^{2} + 4 \cdot 1.0 \cdot (B^{*} \cdot T^{*} - e^{*} \cdot {c^{*}}^{2})}}{2}

c^{*} = K_{y} \cdot \frac{L^{2}}{π^{2} \cdot n^{2}}

a_{z}^{*} = \frac{a_{z}}{n^{2}}

B^{*} = E_{0.05} \cdot I_{Z} \cdot \frac{π^{2} \cdot n^{2}}{L^{2}} + c^{*}

T^{*} = G_{0.05} \cdot I_{T} + c^{*} \cdot e^{2}

n = 1, 2, 3 . . .

M_crit	Critical bending moment
a_z	Distance of the load application from the shear center
e	Distance of the member elastic foundation from the shear center
K_y	Elastic member foundation per truss member
L	Beam length
n	n^th eigensolution
E_0.05	5 % quantile of the modulus of elasticity
I_z	Second moment of area about the weak axis
G_0.05	5 % quantile of the shear modulus
I_T	Torsional constant

Critical Bending Moment

The constant n denotes the 1st, 2nd, 3rd … eigensolution. Thus, several eigensolutions have to be analyzed, and the smallest critical bending moment then governs. The following critical bending moments are the result for n = 1…30.

n	M_crit [kNm]	n	M_crit[kNm]
1	9,523.25	16	2,214.63
2	4,281.26	17	2,339.17
3	2,294.32	18	2,464.92
4	1,605.56	19	2,591.63
5	1,354.68	20	2,719.14
6	1,282.70	21	2,847.30
7	1,294.12	22	2,976.00
8	1,348.81	23	3,105.16
9	1,428.05	24	3,234.71
10	1,522.29	25	3,364.60
11	1,626.24	26	3,494.77
12	1,736.77	27	3,625.20
13	1,851.94	28	3,755.84
14	1,970.50	29	3,886.67
15	2,091.60	30	4,017.68

M_crit becomes minimal for n = 6 and is about 1,282.70 kNm.

The eigenvalue solution from the RF-/FE-LTB add-on module (see Image 07) results in:

M_crit = 3.4376 ⋅ 405 kNm = 1,397.25 kNm

Both results match very well. However, the analytical solution is on the safe side, as this method is based on a constant bending moment distribution. Then, a critical load q_crit is assigned to the constant critical bending moment M_crit.

q_{crit} = \frac{M_{crit} \cdot 8}{L^{2}}

q_crit	Critical load
M_crit	Critical bending moment
L	Beam length

Critical Load

Since the member foundation in this example is regarded as very stiff and constantly distributed over the truss member length, critical bending moments occur that are slightly higher than for the rigid single supports.

According to [3], Chapter 9.2.5.3 (2), stiffening bracings must be stiff enough so that they do not exceed the horizontal deflection of L/500. The calculation must be carried out with the design values of the stiffnesses (see [1], Chapter NCI to 9.2.5.3).

For k_crit = 0.195, H = 5 m and q_p = 0.65 kN/m² as gust velocity pressure, the following loads result (see [3], Chapter 9.2.5.3):

N_{d} = (1 - k_{crit}) \cdot \frac{M_{d}}{h}

N_d	Stabilizing force for compression chord
k_crit	Lateral buckling factor
M_d	Design moment
h	Beam height

Stabilizing Force for Compression Chord

N_d = (1 - 0.195) ⋅ 405 / 1.2 = 271.68 kN

q_{d} = \sqrt{\frac{15}{L}} \cdot \frac{n \cdot N_{d}}{k_{f, 3} \cdot L}

q_d	Stiffening load
n	Number of truss members
L	Beam length
k_f,3	Modification factor for stiffening resistance

Stiffening Load

q_d = 2.76 kN/m

q_{d, Wind} = γ_{Q} \cdot (c_{pe, D} \cdot c_{pe, E}) \cdot q_{p} \cdot \frac{H}{2}

q_d,wind	Design load due to wind
γ_Q	Partial safety factor for a variable action
c_pe	External pressure coefficient
q_p	Peak velocity pressure
h	Height of the building

Design Load due to Wind

q_d,wind = 1.5 ⋅ (0.7 + 0.3) ⋅ 0.65 ⋅ 5 / 2 = 2.44 kN/m

The deformation of the stiffening bracing is shown in Image 08. The loads were divided in half because there are two stiffening bracings.

Horizontal Displacement of Stiffening Bracing

The allowable deformation is:

\frac{L}{500} = \frac{18 m}{500} = 36.00 mm \geq 4.74 mm

Allowable Deformation

The result confirms the assumption of a very stiff bracing and is consistent with the almost identical critical bending moments of the system with rigid intermediate supports and the one with elastic member foundation.

Conclusion

It was shown which possibilities in timber construction can be used to analyze the lateral buckling of bending beams. For common methods, it is important to ensure that the stiffening bracings are stiff enough to accept rigid supports. Options have been shown in this article for cases when this assumption does not apply. Basically, the bending beams and the stiffening bracings have to be designed for their load-bearing capacity and serviceability according to the corresponding standard. However, this is beyond the scope of this article.

Knowledge Base

KB 001669 | Lateral-Torsional Buckling in Timber Construction | Examples 2

Author

Mr. Rehm is responsible for developing products for timber structures, and he provides technical support for customers.

Links

References

DIN. (2013). National Annex – Eurocode 5: Design of Timber Structures – Part 1-1: General – Common Rules and Rules for Buildings, DIN EN 1995-1-1/NA:2013-08. Berlin: Beuth Verlag GmbH.
Petersen, C. (1982). Statik und Stabilität der Baukonstruktionen, (2nd ed.). Wiesbaden: Vieweg.
CEN. (2010). Eurocode 5: Design of Timber Structures – Part 1-1: General – Common Rules and Rules for Buildings; DIN EN 1995-1-1:2010-12. Berlin: Beuth Verlag GmbH.

;