Что такое центральное сжатие?
Сечение конструктивного элемента находится под действием центрального сжатия, если силы, действующие на одной стороне сечения, сокращаются в центре тяжести сечения до единственной силы N. Таким образом, данная нормальная сила N перпендикулярна сечению и направлена в его сторону. В отличие от комбинированного изгиба, такое нагружение никогда не встречается на практике, так как в реальности колонна никогда не подвергается полностью симметричной нагрузке, либо обладает несовершенствами в конструкции, как объясняется в следующей технической статье:
- КБ | Расчет железобетонных колонн, подверженных комбинированному изгибу в модуле RF-CONCRETE Columns
Критерий гибкости для единичных элементов
On admet que les effets du second ordre (imperfections, dissymétrie, etc…) peuvent être négligés si l'élément est sollicité uniquement par un effort normal de compression NEd et si le critère d'élancement est respecté.
Критерий гибкости
λ < λlim
λ ... Коэффициент гибкости
λlim ... Предельная гибкость
Гибкость и полезная длина по норме EN 1992-1-1
| λ | коэффициент гибкости |
| l0 | полезная длина = kcr ⋅ l |
| i | радиус инерции железобетонного профиля без трещин |
| kcr | коэффициент полезной длины = 0,5 ⋅ √ [(1 + k1/(0,45 + k1 )) ⋅ (1 + k2/(0,45 + k2 ))] по формуле (5.15) из 5.8.3.2 |
| l | свободная длина |
| к1 , к2 | коэффициенты гибкости на обоих концах элемента |
Предельная гибкость по норме EN 1992-1-1
Предельная гибкость
λlim = (20 ⋅ A ⋅ B ⋅ C) / √n согласно 5.8.3.1 (1) формула (5.13N)
A = 1 / (1 + 0,2 φef) = 0,7, если φef неизвестно
B = √(1 + 2 ⋅ ω) = 1,1, если ω неизвестно
C = 1,7 - rm = 0,7, если rm неизвестно
n = NEd/(Ac ⋅ fcd ) ... Относительная нормальная сила
φef ... Эффективный коэффициент ползучести
ω ... Механический процент армирования
rm ... соотношение моментов
NEd ... расчетное значение действующей нормальной силы
Ac ... Общая площадь чистого бетонного сечения
fcd ... Расчётное значение прочности бетона на сжатие
Напряжение сжатия в стали
Усадка бетона при осевом сжатии ограничена величиной ε c2 в случае параболическо-прямоугольной диаграммы σ-ε. Благодаря сцеплению бетона и стали, сокращение у арматуры одинаково, и по нему можно определить напряжение.
| σs | напряжение в арматуре |
| fyd | расчетный предел текучести арматурной стали = fyk/γs |
| εc2 | относительная деформация сжатия для максимального напряжения |
| Es | Модуль упругости |
| fyk | нормативный предел текучести |
| γs | Частичный коэфф. запаса стали |
| εud | расчетное значение предельной деформации = fyd/Es |
Сжимающее напряжение в бетоне
Напряжение в бетоне
fcd = αcc ⋅ fck / γc
αcc ... Коэффициент, учитывающий долговременное воздействие на прочность при сжатии
fck ... Нормативная прочность бетона на сжатие
γc ... частный коэффициент надежности по бетону
Размеры бетонного сечения
Сила, которая может быть уравновешена сечением бетона, соответствует его максимальной несущей способности при сжатии, которая напрямую зависит от сечения и расчетной прочности.
Уравновешивающая сила бетона
Fc = Ac ⋅ fcd
Арматура при этом уравновесит оставшуюся центральную сжимающую нагрузку.
Уравновешивающая сила арматуры
Fs = NEd - Fc
По этим двум уравнениям равновесия можно определить расчетное сечение бетона, а затем сечение арматуры.
Площадь бетонного сечения
Ac ≥ NEd / (fcd + As / Ac ⋅ σs)
As = Fs/σs ... площадь сечения арматуры
Применение теории с помощью дополнительного модуля RF-CONCRETE Members
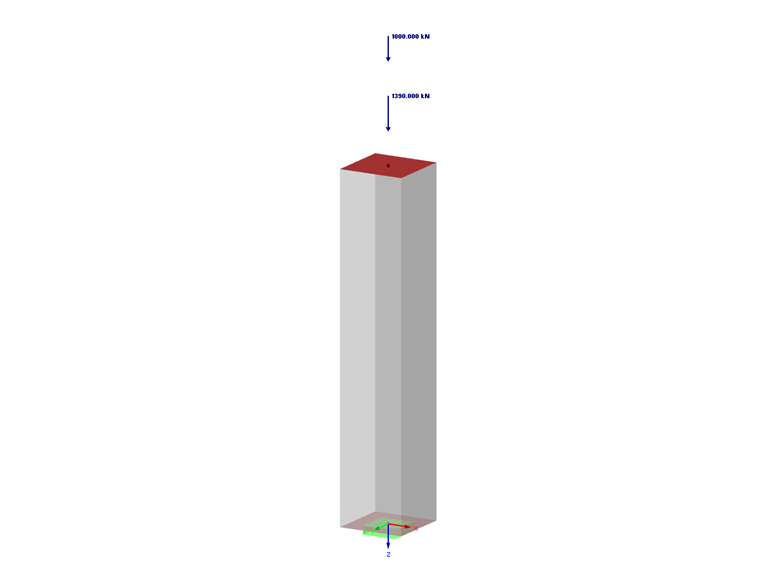
В нашей статье мы проанализируем результаты, полученные автоматически при расчете арматуры. Поскольку необходимо также определить сечение бетона для расчета, основная модель в RFEM 5 будет иметь заданную ширину и неизвестную высоту, большую или равную ширине.
Будем учитывать следующие параметры:
- Постоянные нагрузки: Ng = 1 390 кН
- Переменные нагрузки: Nq = 1000 кН
- Длина колонны: l = 2,1 м
- Подлежащее определению прямоугольное сечение: ширина b = 40 см / неизвестная высота ≥ 40 см
- Собственным весом колонны можно пренебречь.
- Колонна не объединена со связью жесткости.
- Класс бетона по прочности: C25/30
- Сталь: S 500 A для восходящей ветви
- Диаметр продольной арматуры: ϕ = 20 мм
- Диаметр поперечной арматуры: ϕt = 8 мм
- Защитный слой бетона: 3 см
свойства материала
Расчётное значение прочности бетона на сжатие
fcd = 1 ⋅ 25 / 1,5 = 16,7 МПа
Относительная деформация сжатия при максимальном напряжении
εc2 = 2 ‰
Расчетный предел текучести арматурной стали
fyd = 500 / 1,15 = 435 МПа
Предельная деформация в арматуре
εud = fyd / Es = 435 / (2 ⋅ 105) = 2,17 ‰
Напряжение в арматуре
σs = 2 ⋅ 10 5 ⋅ 0,002 = 400 МПа при εc2 < εud
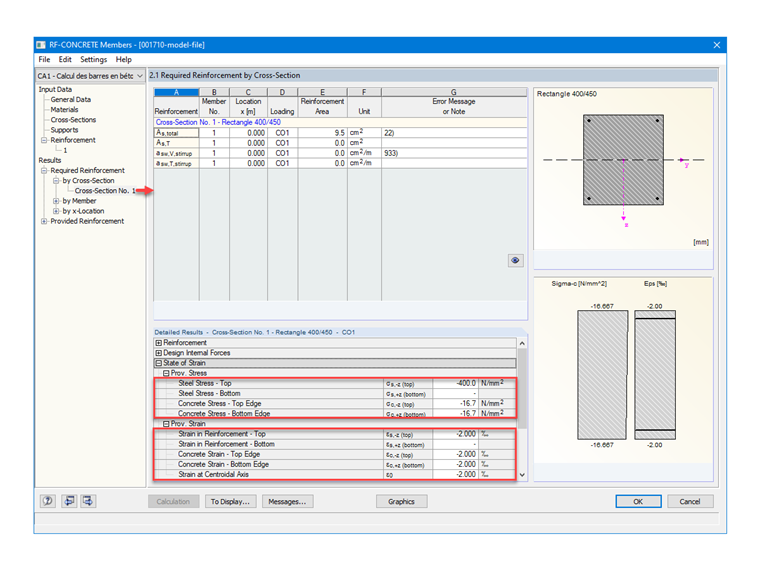
Для проверки настроек материала в RF-CONCRETE Columns на рисунке 02 показаны действующие напряжения и деформации для бетона и требуемой арматуры.
´État Предельное состояние 1-й группы
Расчетные нагрузки в предельном состоянии
NEd = 1,35 ⋅ Ng + 1,5 ⋅ Nq
NEd = 1,35 ⋅ 1390 + 1,5 ⋅ 1000 = 3,38 МН
Эффекты второго порядка не учитываются в предельном состоянии
Для того, чтобы правильно приложить нагрузку в оголовке колонны, мы смоделировали стержень, который защемлен только в основании и свободен в оголовке. Однако мы хотим учесть в расчете то, что колонна в оголовке прикреплена к балкам, при этом предполагается, что колонна обладает более низкой жесткостью, чем балки. Тогда можно считать, что стержень защемлен на обоих концах. Таким образом, теоретически коэффициенты гибкости должны быть равны нулю при идеальном защемлении. Однако на практике идеального защемления не существует. Наоборот, минимальное значение, которое необходимо учитывать для коэффициентов гибкости, равно: k1 или k2 = 0,1.
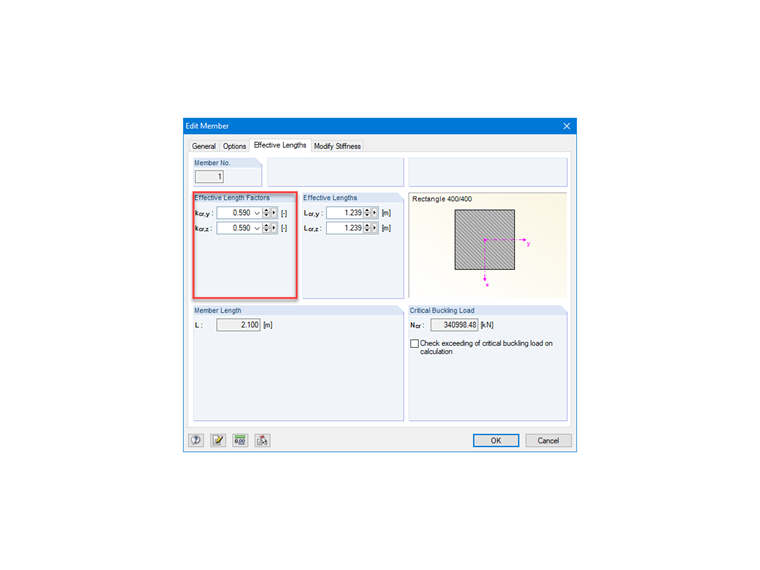
Коэффициент расчётной длины
kcr = 0,5 ⋅ (1 + 0,1 / (0,45 + 0,1)) = 0,59
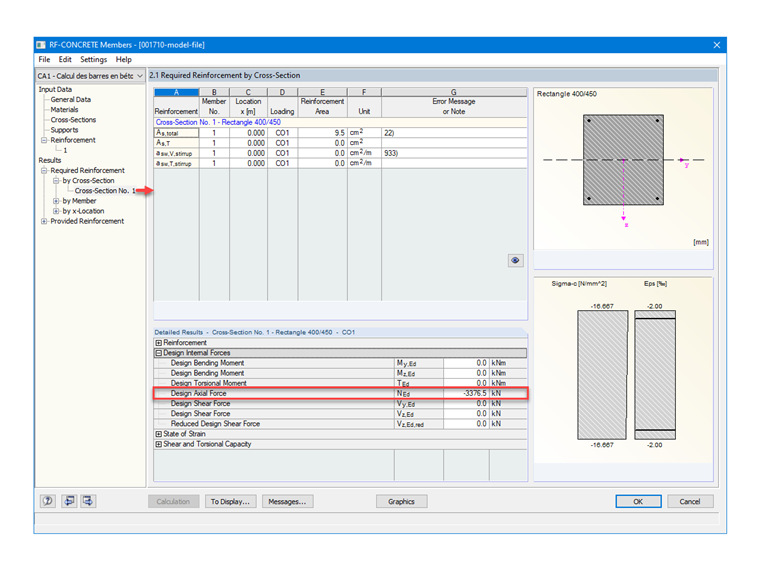
На рисунке 04 показана возможность настройки коэффициента свободной длины для стержневого элемента в программе RFEM.
Поскольку необходимо определить высоту сечения, предполагается, что h > b, и поэтому радиус инерции прямоугольного сечения является определяющим для небольшой ширины.
Радиус определяющей инерции в плоскости, параллельной ширине b = 40 см
iz = b / √12
Гибкость
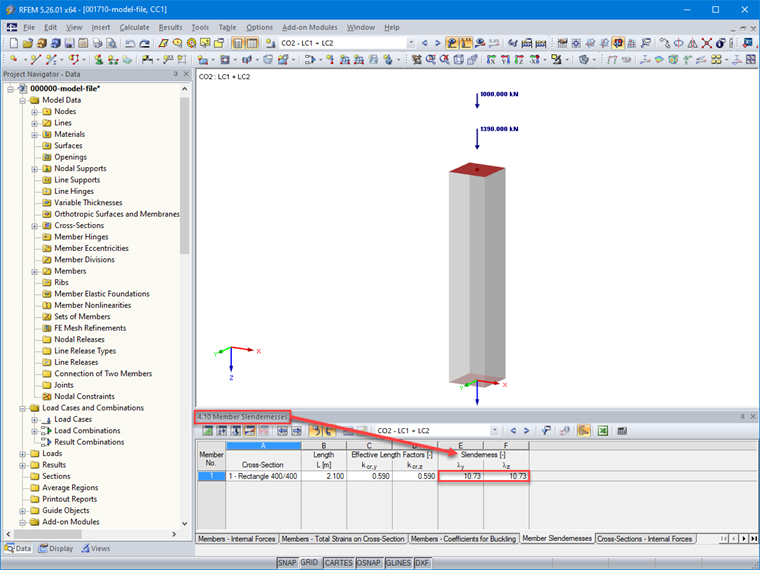
λz = (0,59 ⋅ 2,1 ⋅ √12) / 0,40 = 10,73 м
На рисунке 05 показаны значения гибкости, полученные для стержня в таблице 4.10 после расчета в RFEM.
Чтобы проверить значение гибкости, рассчитаем вручную предельную гибкость, приняв h = b.
Предельная гибкость
n = 3,38 / (0,40² ⋅ 16,7) = 1,26
λlim = 20 ⋅ 0,7 ⋅ 1,1 ⋅ 0,7 / √1,26 = 9,6 м
λz > λlim → условие не выполнено.
Тем не менее, мы все равно будем рассчитывать центральное сжатие, так как из-за небольшого отклонения мы позже отметим, что при определении реальной высоты сечения условие будет выполнено.
Реальная высота, подлежащая расчету
Для определения реальной высоты сечения h можно основываться на следующем предположении для коэффициента армирования: As/Ac = 1 %. Теперь мы можем определить реальное сечение для расчета и его высоту в зависимости от напряжения в арматуре и ширины сечения b.
Площадь бетонного сечения
Ac ≥ 3,38 / (16,7 + 400 / 100) = 0,163 м²
Высота сечения
Ac = b ⋅ h → h ≥ 0,163 / 0,4 = 0,41 м
Условие h > b, принятое для расчета гибкости, выполнено, и мы можем выбрать высоту сечения, кратную 5 см, то есть h = 45 см.
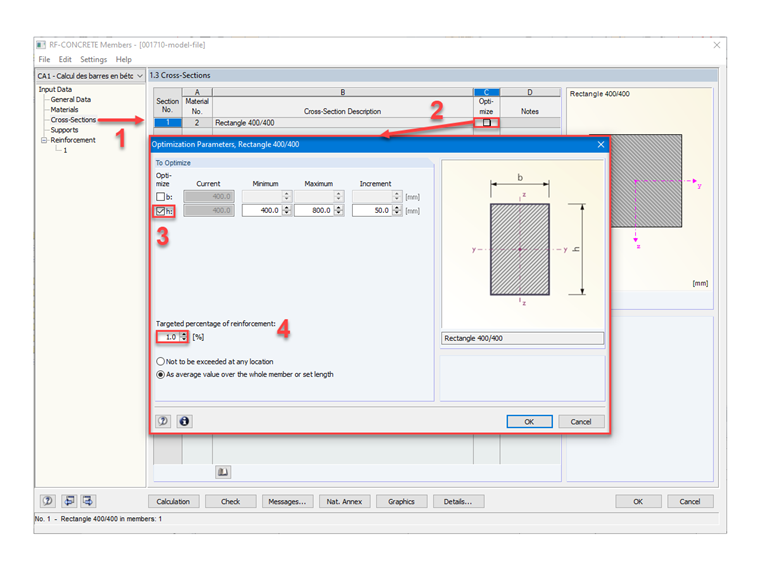
На рисунке 06 показаны шаги автоматического определения высоты прямоугольного сечения в модуле RF-CONCRETE Members с помощью функции «Оптимизировать».
Несущее сечение
Уравновешивающая сила бетона
Fc = 0,40 ⋅ 0,45 ⋅ 16,7 = 3 МН
Уравновешивающая сила арматуры
Fs = 3,376 - 3 = 0,38 МН
Получим соответствующую площадь сечения арматуры:
Площадь арматуры
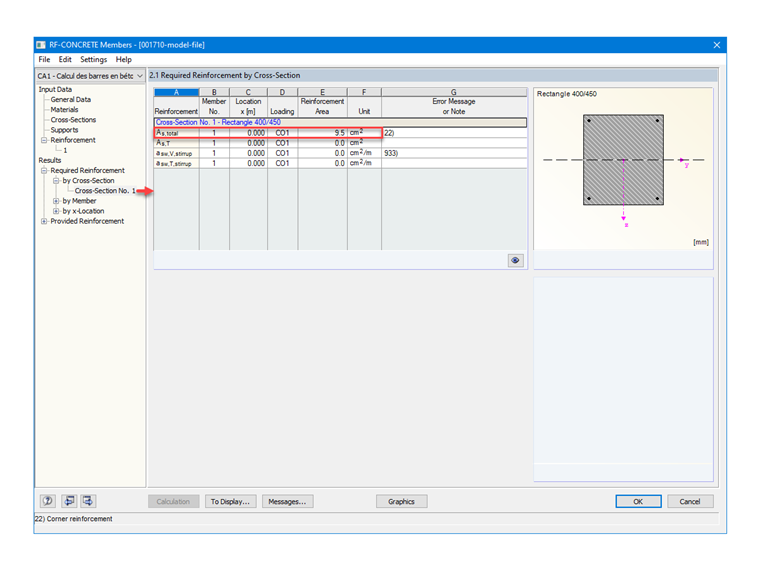
As = 0,38 / 400 ⋅ 104 = 9,5 см²
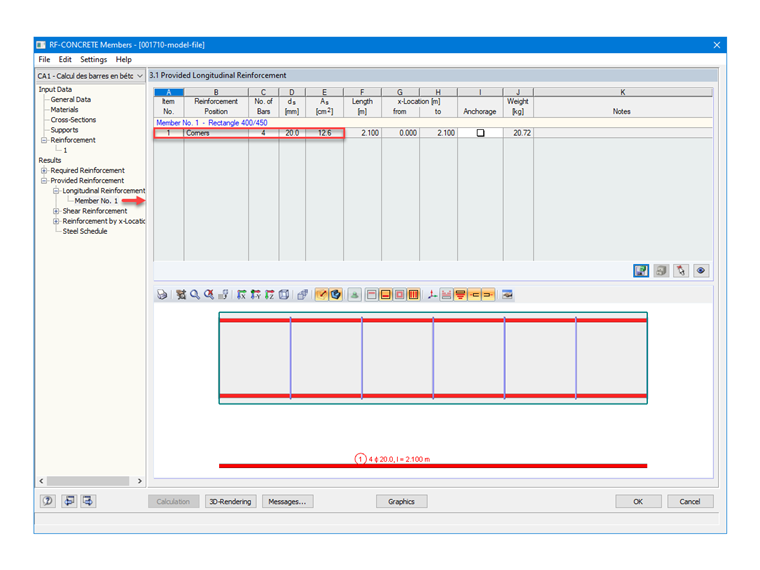
После настройки в модуле RF-CONCRETE Members стали диаметром 20 мм, модуль автоматически определил в ней 4 стержня с распределением арматуры по углам; то есть по 1 HA 20 на угол. Таким образом, результат площади сечения и следующий:
As = 4 ⋅ 3,142 = 12,57 см²
Механический процент армирования
ω = (As ⋅ fyd) / (Ac ⋅ fcd) = 12,57 ⋅ 435 / (40 ⋅ 45 ⋅ 16,7) = 0,182
Окончательная проверка предельной гибкости при h > b
n = 3,38 / (0,40 ⋅ 0,45 ⋅ 16,7) = 1,125
B = √(1 + 2 ⋅ ω) = 1,17
λlim = 20 ⋅ 0,7 ⋅ 1,17 ⋅ 0,7 / √1,125 = 10,81 м
λz < λlim → критерий гибкости выполнен.
Применение в других дополнительных модулях
Дополнительный модуль RF-CONCRETE Columns также позволяет определять параметры арматуры конструктивного элемента, подверженного центральному сжатию. Техническую статью с подробным описанием различий по сравнению с RF-CONCRETE Members можно найти здесь:
