C'est quoi la compression centrée ?
Une section d'un élément est sollicitée en compression centrée lorsque les forces agissant d'un côté de la section sont réduites au centre de gravité de la section en une force unique N. Cet effort normal N est alors perpendiculaire à la section et dirigé vers la section. Cette sollicitation ne se rencontre jamais en pratique à l'inverse de la flexion composée, car un poteau réel est toujours soumis soit à la dissymétrie du chargement, soit aux imperfections d'exécution comme on peut le voir dans cet article techniqu.
Critère d'élancement pour les éléments isolés
On admet que les effets du second ordre (imperfections, dissymétrie, etc…) peuvent être négligés si l'élément est sollicité uniquement par un effort normal de compression NEd et si le critère d'élancement est respecté.
Critère d'élancement
λ < λlim
λ ... Coefficient d'élancement
λlim ... Élancement limite
Élancement et longueur efficace selon l'EN 1992-1-1
|
λ |
Coefficient d'élancement |
|
l0 |
Longueur efficace = kcr ⋅ l |
|
i |
Rayon de giration de la section de béton non fissurée |
|
kcr |
Facteur de longueur efficace = 0,5 ⋅ √[(1 + k1 / (0,45 + k1)) ⋅ (1 + k2 / (0,45 + k2))] selon 5.8.3.2(3) formule (5.15) |
|
l |
Longueur libre |
|
k1, k2 |
Coefficients de souplesse aux deux extrémités de l'élément |
Élancement limite selon l'EN 1992-1-1
Élancement limite
λlim = (20 ⋅ A ⋅ B ⋅ C) / √n selon 5.8.3.1(1) formule (5.13N)
A = 1 / (1 + 0,2 φef) = 0,7 si φef est inconnu
B = √(1 + 2 ⋅ ω) = 1,1 si ω est inconnu
C = 1,7 - rm = 0,7 si rm est inconnu
n = NEd / (Ac ⋅ fcd) ... Effort normal relatif
φef ... Coefficient de fluage effectif
ω ... Ratio mécanique d'armatures
rm ... Rapport des moments
NEd ... Valeur de calcul de l'effort normal agissant
Ac ... Aire totale de la section de béton seul
fcd ... Valeur de calcul de la résistance en compression du béton
Contrainte de compression dans l'acier
Le raccourcissement du béton sous compression centrée est limité à εc2 dans le cas du diagramme σ-ε parabole-rectangle. Par adhérence du béton et de l'acier, les raccourcissements sont identiques pour les armatures et on peut en déduire leur contrainte.
|
σs |
Contrainte dans l'armature |
|
fyd |
Limite d'élasticité de calcul de l'acier de béton armé = fyk / γs |
|
εc2 |
Déformation relative en compression pour la contrainte maximale |
|
Es |
Module d'élasticité |
|
fyk |
Limite d'élasticité caractéristique |
|
γs |
Coefficient partiel de l'acier |
|
εud |
Déformation limite de calcul = fyd / Es |
Contrainte de compression dans le béton
Contrainte dans le béton
fcd = αcc ⋅ fck / γc
αcc ... Facteur tenant compte des effets à long terme sur la résistance en compression
fck ... Résistance caractéristique en compression du béton
γc ... Coefficient partiel relatif au béton
Dimensions de la section de béton
La force que peut équilibrer la section de béton correspond à sa capacité portante maximale en compression qui dépend directement de sa section et de sa résistance de calcul.
Force d'équilibre du béton
Fc = Ac ⋅ fcd
Les armatures vont alors équilibrer le reste de la charge de compression centrée.
Force d'équilibre des armatures
Fs = NEd - Fc
À partir de ces deux équations d'équilibre, on peut en déduire la section de béton à dimensionner, puis celle des armatures.
Aire de la section de béton
Ac ≥ NEd / (fcd + As / Ac ⋅ σs)
As = Fs / σs ... Aire de la section d'armature
Application de la théorie avec le module additionnel RF-CONCRETE Members
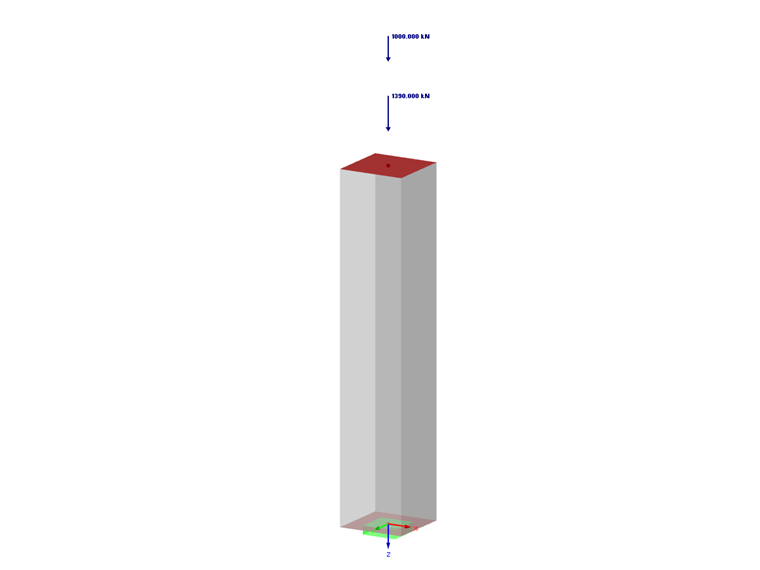
Dans cet article, nous allons analyser les résultats obtenus automatiquement lors du calcul des armatures. L'objectif étant également de déterminer la section de béton à dimensionner, le modèle de base RFEM 5 aura une largeur définie et une hauteur inconnue supérieure ou égale à la largeur.
On va considérer les paramètres ci-après :
- Charges permanentes : Ng = 1 390 kN
- Charges variables : Nq = 1 000 kN
- Longueur poteau : l = 2,1 m
- Section rectangulaire à déterminer : largeur b = 40 cm / hauteur inconnue ≥ 40cm
- Poids propre du poteau négligeable.
- Poteau non intégré au contreventement.
- Classe de résistance du béton : C25/30
- Aciers : S 500 A à palier incliné
- Diamètre des armatures longitudinales : ϕ = 20 mm
- Diamètre des armatures transversales : ϕt = 8 mm
- Enrobage : 3 cm
Caractéristique des matériaux
Valeur de calcul de la résistance en compression du béton
fcd = 1 ⋅ 25 / 1,5 = 16,7 MPa
Déformation relative en compression pour la contrainte maximale
εc2= 2 ‰
Limite d'élasticité de calcul de l'acier de béton armé
fyd = 500 / 1,15 = 435 MPa
Déformation limite dans l'armature
εud = fyd / Es = 435 / (2 ⋅ 105) = 2,17 ‰
Contrainte dans l'armature
σs = 2 ⋅ 105 ⋅ 0,002 = 400 MPa car εc2 < εud
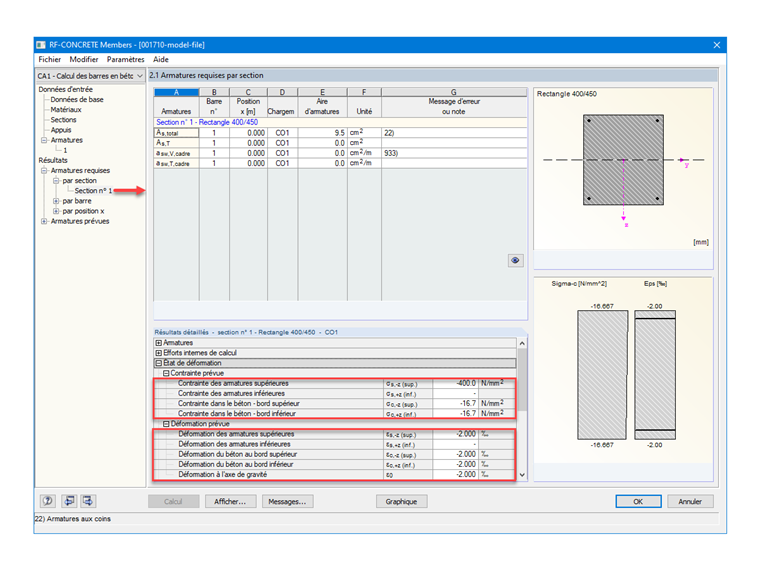
Afin de vérifier le paramétrage des matériaux sur RF-CONCRETE Members, la figure 02 affiche les contraintes et les déformations prévues pour le béton et les armatures requises.
´État limite ultime
Sollicitations de calculs à l'état limite ultime
NEd = 1,35 ⋅ Ng + 1,5 ⋅ Nq
NEd = 1,35 ⋅ 1390 + 1,5 ⋅ 1000 = 3,38 MN
Non prise en compte des effets du second ordre à l'ELU
Dans notre modèle, afin de pouvoir appliquer correctement une charge en tête de poteau, nous avons modélisé une barre uniquement encastrée en pied et libre en tête. Cependant, nous voulons prendre en compte que le poteau est fixé en tête à des poutres avec l'hypothèse que le poteau est moins raide que les poutres. Nous pouvons alors considérer que la barre est encastrée à ses deux extrémités. Ainsi, dans la théorie, les coefficients de souplesse devraient être nuls pour un encastrement parfait. Or, dans la pratique, les encastrements parfaits n'existent pas. La valeur minimale à considérer pour les coefficients de souplesse est donc : k1 ou k2 = 0,1.
Facteur de longueur efficace
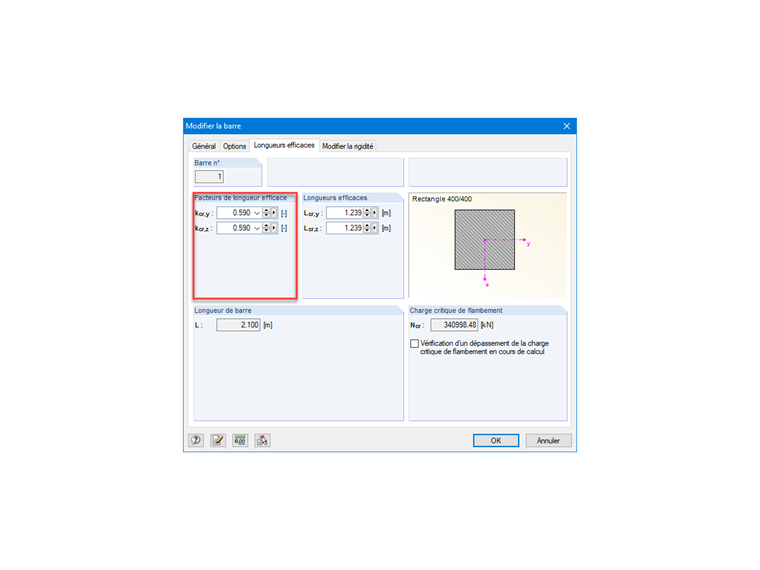
kcr = 0,5 ⋅ (1 + 0,1 / (0,45 + 0,1)) = 0,59
La figure 04 montre la possibilité sur RFEM de paramétrer le facteur de longueur efficace pour un élément de type barre.
La hauteur de la section étant à déterminer, on suppose que h > b et donc que le rayon d'inertie d'une section rectangulaire est plus déterminant pour la petite largeur.
Rayon d'inertie déterminant dans le plan parallèle à la largeur b = 40 cm
iz = b / √12
Élancement
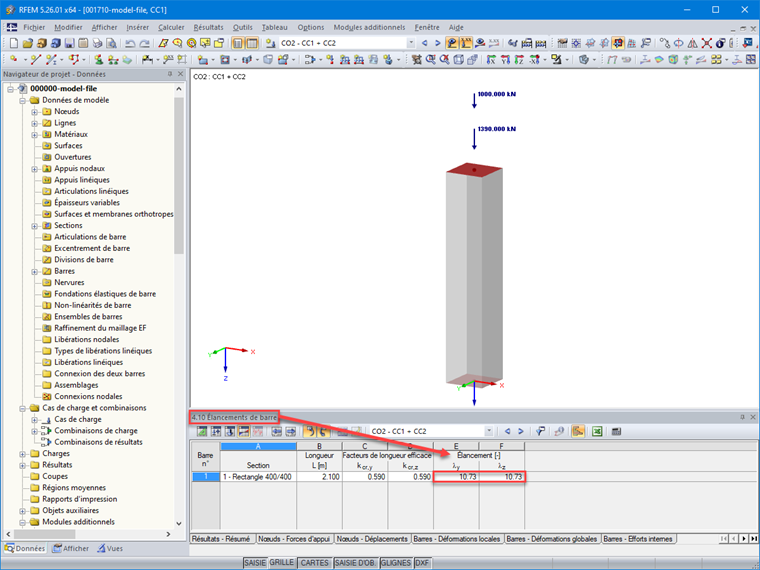
λz = (0,59 ⋅ 2,1 ⋅ √12) / 0,40 = 10,73 m
La figure 05 montre les valeurs d'élancement déterminées pour la barre après calcul dans le tableau 4.10 de RFEM.
Pour vérifier notre élancement, nous déterminons manuellement l'élancement limite, avec l'hypothèse h = b.
Élancement limite
n = 3,38 / (0,40² ⋅ 16,7) = 1,26
λlim = 20 ⋅ 0,7 ⋅ 1,1 ⋅ 0,7 / √1,26 = 9,6 m
λz > λlim → La condition n'est pas respectée.
Cependant, nous allons tout de même calculer en compression centrée car, l'écart étant faible, nous constatons par la suite qu'avec la détermination de la hauteur réelle de section, la condition sera respectée.
Hauteur réelle à calculer
Afin de déterminer la hauteur réelle h de la section, on peut adopter l'hypothèse suivante pour le ratio d'armatures à considérer : As / Ac = 1 %. On peut alors en déduire la section réelle à calculer et sa hauteur en fonction de la contrainte dans les armatures et de la largeur de la section b.
Aire de la section de béton
Ac ≥ 3,38 / (16,7 + 400 / 100) = 0,163 m²
Hauteur de la section
Ac = b ⋅ h → h ≥ 0,163 / 0,4 = 0,41 m
L'hypothèse h > b faite pour le calcul de l'élancement est correcte, et nous pouvons retenir une hauteur de section en choisissant un multiple de 5 cm, soit h = 45 cm.
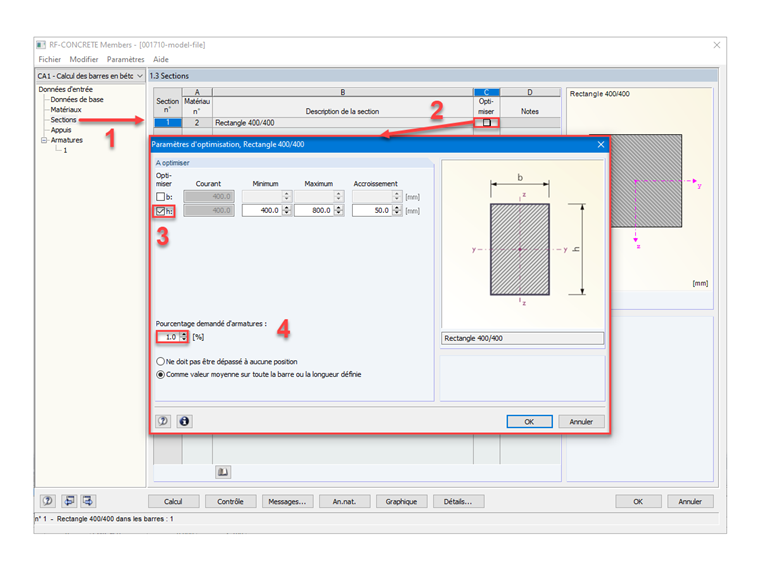
La figure 06 décrit les étapes pour déterminer automatiquement la hauteur de la section rectangulaire sur RF-CONCRETE Members, à l'aide de la fonction « optimiser ».
Section résistante
Force d'équilibre du béton
Fc = 0,40 ⋅ 0,45 ⋅ 16,7 = 3 MN
Force d'équilibre des armatures
Fs= 3,376 - 3 = 0,38 MN
On en déduit la section d'armatures correspondantes :
Aire de la section d'armatures
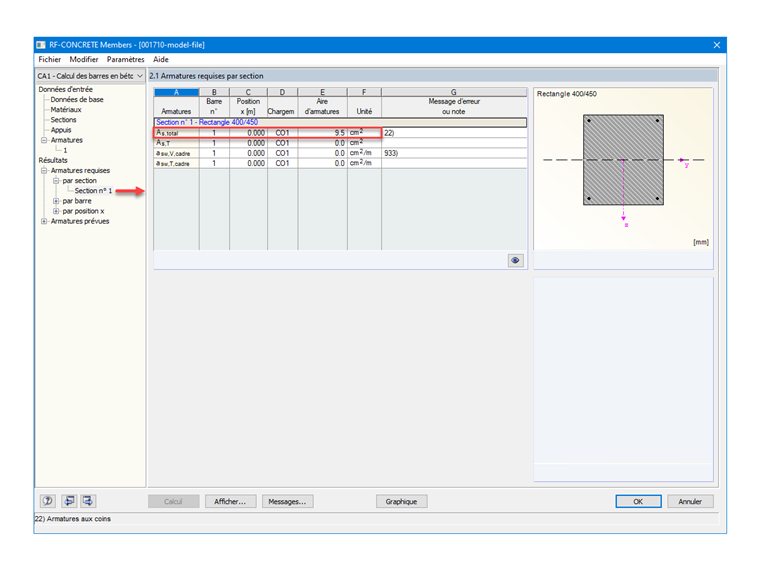
As = 0,38 / 400 ⋅ 104 = 9,5 cm²
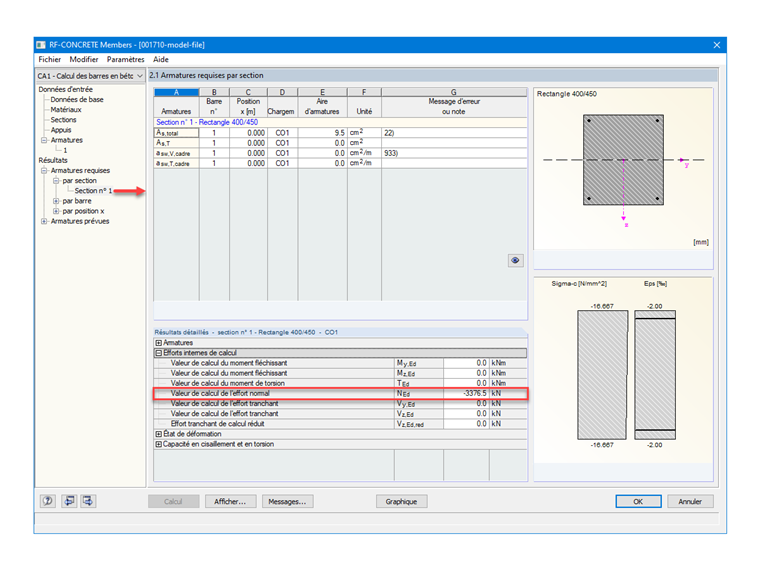
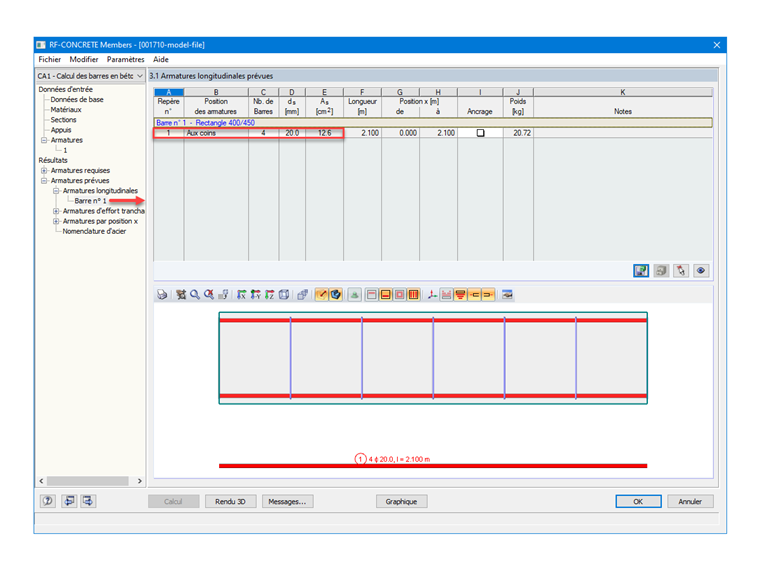
En ayant paramétré des aciers de diamètre 20 mm dans RF-CONCRETE Members, les armatures prévues et déterminées automatiquement par le module sont 4 barres, avec une répartition dans les coins, comme demandé, soit 1 HA 20 par coin. En conséquence, le résultat de l'aire de section d'armatures et la suivante :
As = 4 ⋅ 3,142 = 12,57 cm²
Ratio mécanique d'armatures
ω = (As ⋅ fyd) / (Ac ⋅ fcd) = 12,57 ⋅ 435 / (40 ⋅ 45 ⋅ 16,7) = 0,182
Vérification finale de l'élancement limite car h > b
n = 3,38 / (0,40 ⋅ 0,45 ⋅ 16,7) = 1,125
B = √(1 + 2 ⋅ ω) = 1,17
λlim = 20 ⋅ 0,7 ⋅ 1,17 ⋅ 0,7 / √1,125 = 10,81 m
λz < λlim → Le critère d'élancement est respecté.
Application dans les autres modules
Le module RF-CONCRETE Columns permet également de déterminer les armatures pour un élément en compression centrée. Un article technique détaillant les différences avec RF-CONCRETE Members est disponible ici: