Wymiarowanie słupów betonowych poddanych ściskaniu osiowemu w RFEM 5 z wykorzystaniem RF-CONCRETE Members

Co to jest ściskanie osiowe?

Przekrój elementu konstrukcyjnego jest poddawany ściskaniu osiowemu, gdy siły działające po jednej stronie przekroju zostają zredukowane w środku ciężkości przekroju do pojedynczej siły N. Siła normalna N jest zatem prostopadła do przekroju i skierowana w jego kierunku. W przeciwieństwie do zginania złożonego, naprężenie to nigdy nie występuje w praktyce, ponieważ rzeczywisty słup zawsze jest poddany asymetrii obciążenia lub imperfekcjom w konstrukcji słupa, jak pokazano w tym artykule technicznym:

• Kb | Obliczanie słupów betonowych poddanych zginaniu kombinowanemu za pomocą modułu RF-CONCRETE Columns

Kryterium smukłości dla elementów izolowanych

On admet que les effets du second ordre (imperfections, dissymétrie, etc…) peuvent être négligés si l'élément est sollicité uniquement par un effort normal de compression N_Ed et si le critère d'élancement est respecté.

Kryterium smukłości
λ < λ_lim
λ ... Współczynnik smukłości
λ_lim ... Smukłość graniczna

Smukłość i długość efektywna zgodnie z EN 1992-1-1

Smukłość graniczna zgodnie z EN 1992-1-1

Smukłość graniczna
λ_lim = (20 ⋅ A ⋅ B ⋅ C)/√n zgodnie z 5.8.3.1(1) wzór (5.13N)

A = 1/(1 + 0,2 φ_ef ) = 0,7, jeśli φ_ef jest nieznany
B = √(1 + 2 ⋅ ω) = 1,1, jeżeli ω jest nieznany
C = 1,7 - r_m = 0,7, jeżeli r_m jest nieznane
n = N_Ed/(A_c ⋅ f_cd ) ... Względna siła normalna
φ_ef ... Efektywny współczynnik pełzania
... Intensywność zbrojenia
r_m ... Stosunek momentów
N_Ed ... Obliczeniowa wartość działającej siły osiowej

_C ... Całkowite pole przekroju czystego betonu
F_cd ... Obliczeniowa wartość wytrzymałości betonu na ściskanie

Naprężenie ściskające w stali

W przypadku wykresu σ-ε parabola-prostokąt skurcz betonu pod wpływem ściskania osiowego jest ograniczony do ε_c2. Dzięki tarciu statycznemu betonu i stali skrócenie jest identyczne dla zbrojenia i możemy wydedukować jego naprężenie.

Naprężenie ściskające w betonie

Naprężenie w betonie
f_cd = α_cc ⋅ f_ck/γ_c
α_cc ... Współczynnik uwzględniający wpływ oddziaływań długotrwałych na wytrzymałość na ściskanie
F_ck ... Charakterystyczna wytrzymałość betonu na ściskanie
γ_C ... Częściowy współczynnik bezpieczeństwa odniesiony do betonu

Wymiary przekroju betonowego

Siła, jaką może zrównoważyć betonowy przekrój, odpowiada jego maksymalnej nośności na ściskanie, która zależy bezpośrednio od przekroju i obliczeniowej nośności.

Siła równowagi w betonie
F_c = A_c f_cd

Zbrojenie równoważy pozostałe osiowe obciążenie ściskające.

Siła równowagi w zbrojeniu
F_s = N_Ed - F_c

Na podstawie tych dwóch równań równowagi można wywnioskować, który przekrój betonu ma zostać obliczony, a następnie przekroju stali zbrojeniowej.

Pole przekroju betonowego
A_c ≥ N_Ed/(f_cd + A_s/A_c ⋅ σ_s )
A_s = F_s/σ_s ... Pole przekroju zbrojenia

Zastosowanie teorii z wykorzystaniem RF-CONCRETE Members

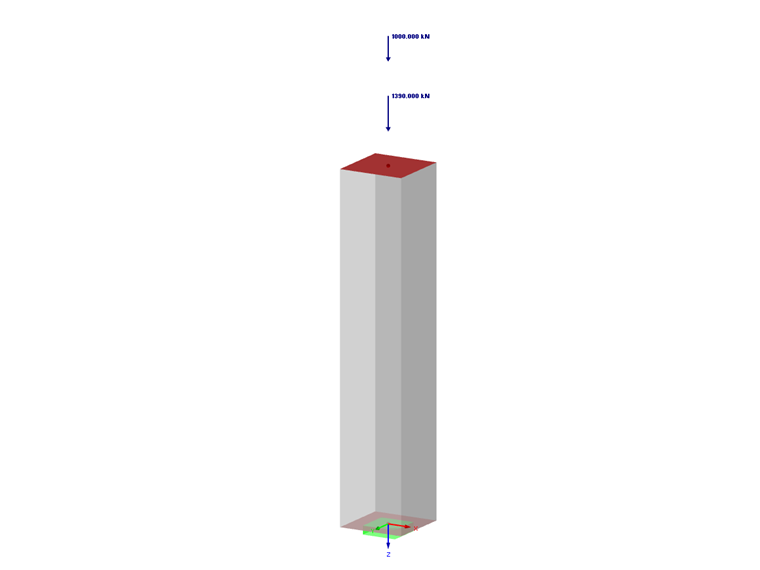
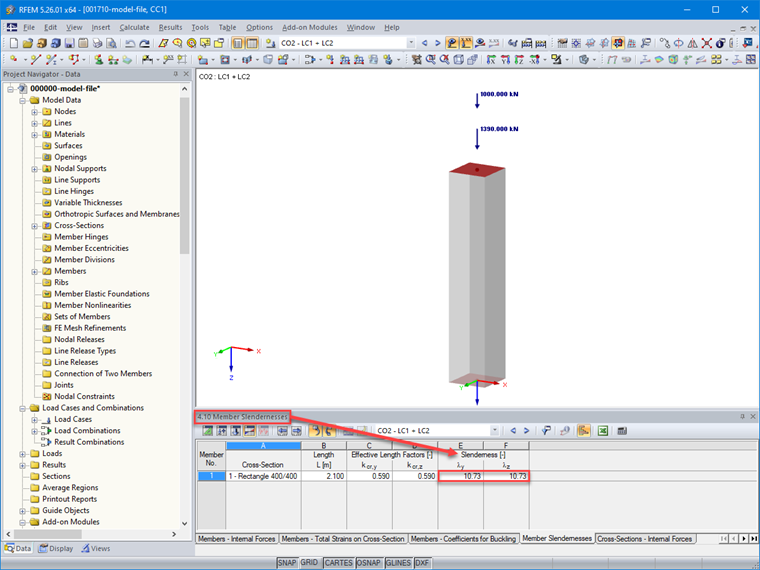
W tym artykule przeanalizujemy wyniki uzyskane automatycznie do obliczeń zbrojenia. Ponieważ celem jest również określenie przekroju betonu, który ma zostać obliczony, model podstawowy programu RFEM 5 ma określoną szerokość i nieznaną wysokość równą lub większą od szerokości.

Uwzględnimy następujące parametry:

• Obciążenia stałe: N_g = 1,390 kN
• Obciążenia zmienne: N_q = 1,000 kN
• Długość słupa: l = 2,1 m²
• Przekrój prostokątny do określenia: szerokość b = 40 cm/nieznana wysokość ≥ 40 cm
• Ciężar własny słupa' można zignorować.
• Słup nie jest zintegrowany ze stężeniem.
• Klasa wytrzymałości betonu: C25/30
• Stal: S 500 A wykres ze wzmocnieniem
• Średnica zbrojenia podłużnego: ϕ = 20 mm
• Średnica zbrojenia poprzecznego: ϕt = 8 mm
• Otulina betonowa: 3 cm

właściwości materiałowe

Obliczeniowa wartość wytrzymałości betonu na ściskanie
f_cd = 1 ⋅ 25/1,5 = 16,7 MPa

Względne odkształcenie ściskające dla maksymalnego naprężenia
ε_c2 = 2

Obliczeniowa granica plastyczności stali zbrojeniowej
f_yd = 500/1,15 = 435 MPa

Odkształcenie graniczne w zbrojeniu
ε_ud = f_yd/E_s = 435/(2 ⋅ 10⁵ ) = 2,17 ‰

Naprężenie w zbrojeniu
σ_s = 2 ⋅ 10⁵ ⋅ 0,002 = 400 MPa gdy ε_c2 < ε_ud

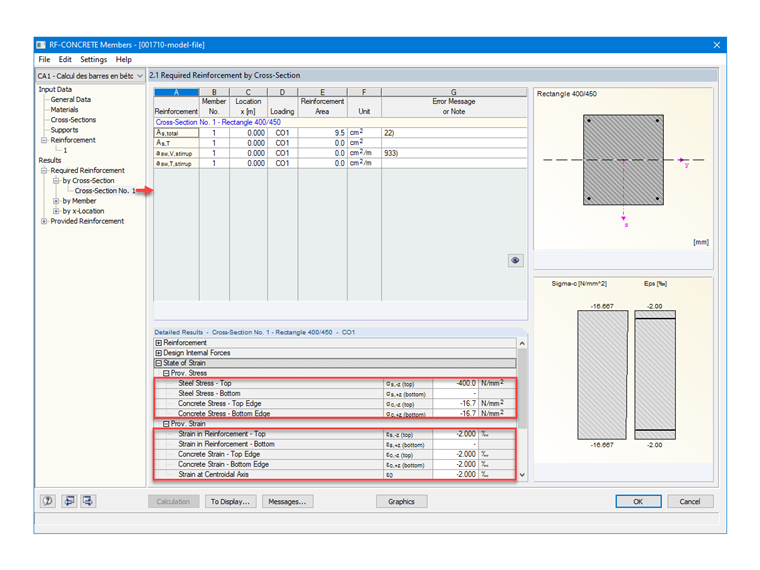
W celu sprawdzenia ustawień materiałowych w RF-CONCRETE Columns, rysunek 02 przedstawia oczekiwane naprężenia i odkształcenia dla betonu oraz wymaganego zbrojenia.

´État Stan graniczny nośności

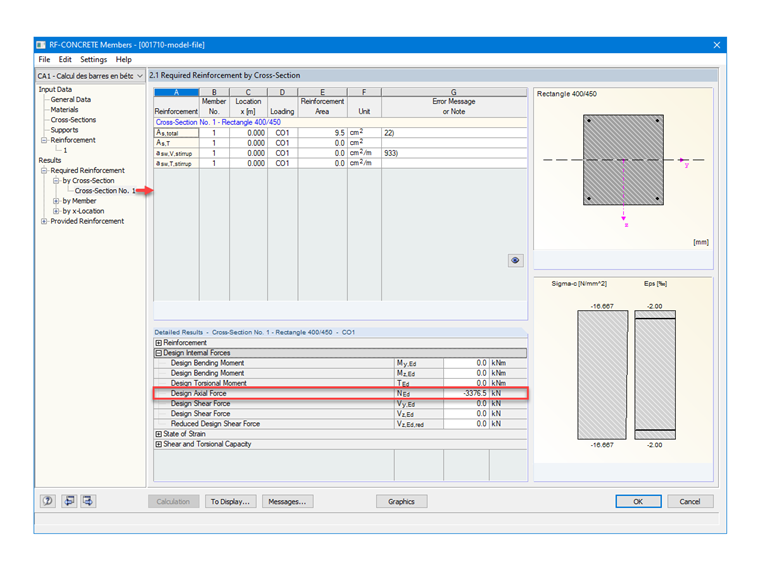
Obciążenia obliczeniowe w stanie granicznym nośności
N_Ed = 1,35 ⋅ N_g + 1,5 ⋅ N_q
N_Ed = 1,35 ⋅ 1390 + 1,5 ⋅ 1000 = 3,38 MN

Efekty drugiego rzędu nie są uwzględniane w SGN

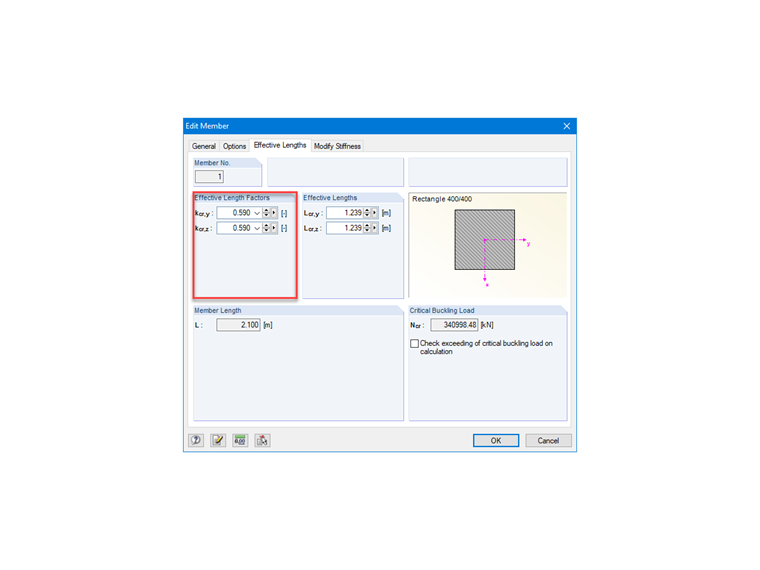
Aby prawidłowo przyłożyć obciążenie u szczytu słupa, zamodelowaliśmy pręt, który jest utwierdzony tylko u podstawy i jest swobodny w głowicy. Chcemy jednak uwzględnić słup mocowany w górnej części do niektórych belek, zakładając, że słup jest mniej sztywny niż belki. Możemy wówczas uznać, że pręt jest utwierdzony na obu końcach. Zatem teoretycznie współczynniki podatności powinny wynosić zero, aby uzyskać idealne utwierdzenie. Jednak w praktyce nie ma idealnego utwierdzenia. Dlatego minimalna wartość współczynników podatności, jaką należy uwzględnić, wynosi: k₁ lub k₂ = 0,1.

Współczynnik długości efektywnej
k_cr = 0,5 ⋅ (1 + 0,1/(0,45 + 0,1)) = 0,59

Rysunek 04 pokazuje możliwość ustawienia współczynnika długości wyboczeniowej dla elementu typu pręt w programie RFEM.

Ze względu na konieczność określenia wysokości przekroju przyjmuje się, że h > b, a zatem promień bezwładności przekroju prostokątnego jest bardziej decydujący dla małej szerokości.

Promień decydującego momentu bezwładności w płaszczyźnie równoległej do szerokości b = 40 cm
i_z = b/√12

smukłość
λ_z = (0,59 ⋅ 2,1 ⋅ 12)/0,40 = 10,73 m

Rysunek 05 przedstawia wartości smukłości pręta wyznaczone po obliczeniach w tabeli 4.10 programu RFEM.

Aby zweryfikować naszą smukłość, ręcznie określamy smukłość graniczną, zakładając h = b.

Smukłość graniczna
n = 3,38/(0,40² ⋅ 16,7) = 1,26
λ_lim = 20 ⋅ 0,7 ⋅ 1,1 ⋅ 0,7/√1,26 = 9,6 m
λ_z > λ_lim → Warunek nie jest spełniony.

Jednak nadal będziemy przeprowadzać obliczenia przy ściskaniu centrycznym, ponieważ ze względu na niewielką odchyłkę, jak później zauważymy, warunek zostanie spełniony przy określeniu rzeczywistej wysokości przekroju.

Rzeczywista wysokość do obliczenia

W celu wyznaczenia rzeczywistej wysokości h przekroju, można przyjąć następującą hipotezę, uwzględniającą stopień zbrojenia: As_/Ac = 1%. Możemy wówczas wyprowadzić rzeczywisty przekrój do obliczenia i jego wysokość jako funkcję naprężenia w zbrojeniu i szerokości przekroju b.

Pole przekroju betonowego
A_c ≥ 3,38/(16,7 + 400/100) = 0,163 m²

Wysokość profilu
A_c = b h → h ≥ 0,163/0,4 = 0,41 m

Założenie h > b przyjęte dla obliczeń smukłości jest prawidłowe, a możemy zachować wysokość przekroju, wybierając wielokrotność 5 cm; czyli h = 45 cm.

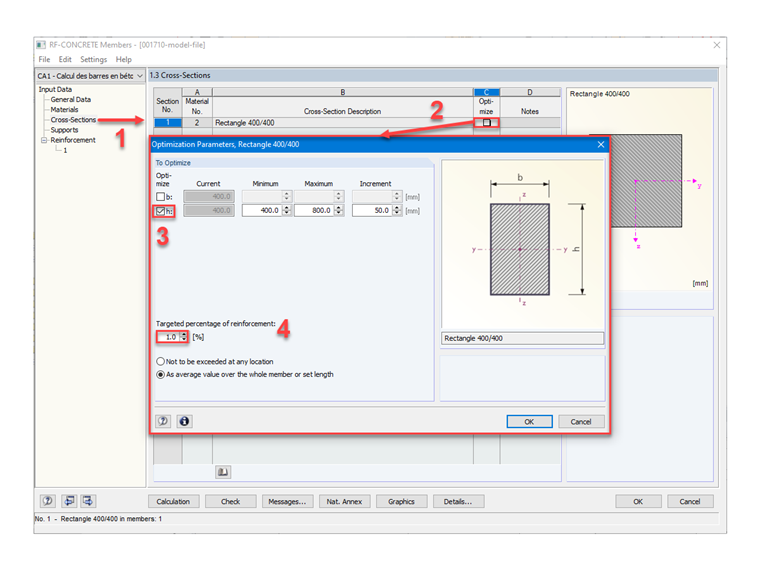
Rysunek 06 przedstawia kolejne kroki, aby automatycznie określić wysokość przekroju prostokątnego w RF-CONCRETE Members za pomocą funkcji "Optymalizuj".

Przekrój nośny

Siła równowagi w betonie
Fc = 0,40 ⋅ 0,45 ⋅ 16,7 =₃ MN

Siła równowagi w zbrojeniu
F_s = 3,376 - 3 = 0,38 MN

Wyliczamy odpowiednie pole przekroju zbrojenia:

Pole przekroju zbrojenia
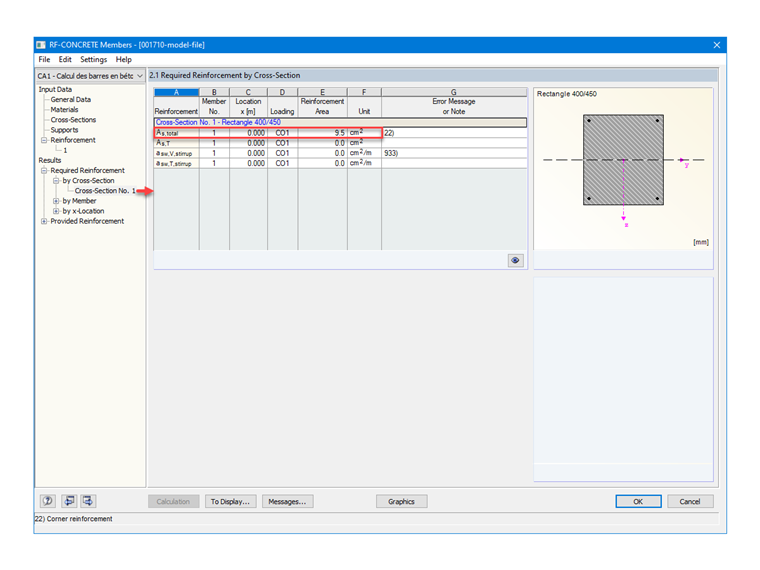
A_s = 0,38/400 ⋅ 10⁴ = 9,5 cm²

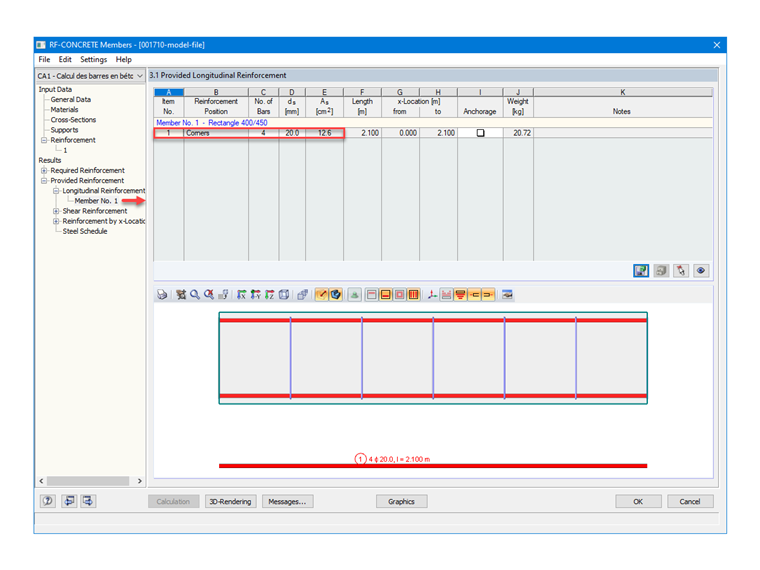
Po ustawieniu w RF-CONCRETE Members stalowych o średnicy 20 mm, moduł zbrojenia wyznaczony i zdefiniowany automatycznie to 4 pręty, z rozkładem w narożach zgodnie z życzeniem użytkownika; tj. 1 HA 20 na naroże. Dlatego oblicza się pole przekroju oraz:

A_s = 4 ⋅ 3,142 = 12,57 cm²

Intensywność zbrojenia
ω = (A_s ⋅ f_yd )/(A_c ⋅ f_cd ) = 12,57 ⋅ 435/(40 ⋅ 45 ⋅ 16,7) = 0,182

Końcowe sprawdzenie smukłości granicznej jako h > b
n = 3,38/(0,40 ⋅ 0,45 ⋅ 16,7) = 1,125
B = √(1 + 2 ⋅ ω) = 1,17
λ_lim = 20 ⋅ 0,7 ⋅ 1,17 ⋅ 0,7/√1,125 = 10,81 m
λ_z < λ_lim → Kryterium smukłości jest spełnione.

Zastosowanie w innych modułach dodatkowych

Moduł dodatkowy RF-CONCRETE Columns umożliwia również definiowanie zbrojenia elementu konstrukcyjnego poddanego ściskaniu osiowemu. Tutaj można znaleźć artykuł techniczny wyjaśniający różnice między RF-CONCRETE Members a RF-CONCRETE Columns:

• Kb | Wymiarowanie słupów betonowych poddanych ściskaniu osiowemu w RF-CONCRETE Columns