Was ist eine zentrische Druckbeanspruchung?
Der Querschnitt eines Bauteils ist zentrisch druckbeansprucht, wenn die Kräfte, die auf einer Seite des Profils wirken, im Schwerpunkt des Querschnitts auf eine einzige Kraft N reduziert sind. Diese Normalkraft N steht also senkrecht zum Querschnitt und ist auf den Querschnitt gerichtet. Im Gegensatz zur kombinierten Biegung ist diese Beanspruchung in der Praxis nie anzutreffen, da eine Stütze in Wirklichkeit nie ganz symmetrisch belastet wird oder Imperfektionen in der Bauausführung unterliegt, wie in diesem Fachbeitrag beschrieben ist:
Schlankheitsgrad bei Einzelelementen
Es wird davon ausgegangen, dass die Auswirkungen nach Theorie II. Ordnung (Imperfektionen, fehlende Symmetrie etc.) vernachlässigt werden können, wenn das Element nur mit einer Drucknormalkraft NEd beansprucht wird und das Schlankheitskriterium erfüllt ist.
Schlankheitskriterium
λ < λlim
λ ... Schlankheitsgrad
λlim ... Grenzschlankheit
Schlankheit und effektive Länge nach EN 1992-1-1
| λ | Schlankheitsgrad |
| l0 | effektive Länge = kcr ⋅ l |
| i | Trägheitsradius des ungerissenen Betonquerschnitts |
| kcr | Knicklängenbeiwert = 0,5 ⋅ √[(1 + k1 / (0,45 + k1)) ⋅ (1 + k2 / (0,45 + k2))] gemäß 5.8.3.2(3) Formel (5.15) |
| l | freie Länge |
| k1, k2 | Biegsamkeitskoeffizienten an beiden Enden des Elements |
Grenzwert der Schlankheit nach EN 1992-1-1
Grenzschlankheit
λlim = (20 ⋅ A ⋅ B ⋅ C) / √n gemäß 5.8.3.1(1) Formel (5.13N)
A = 1 / (1 + 0,2 φef) = 0,7 falls φef nicht bekannt ist
B = √(1 + 2 ⋅ ω) = 1,1 falls ω nicht bekannt ist
C = 1,7 - rm = 0,7 falls rm nicht bekannt ist
n = NEd/(Ac ⋅ fcd ) … Relative Normalkraft
φef ... Effektive Kriechzahl
ω ... Mechanischer Bewehrungsgrad
rm ... Momentenverhältnis
NEd ... Bemessungswert der einwirkenden Normalkraft
Ac ... Gesamtfläche des Betonquerschnitts
fcd ... Bemessungswert der Druckfestigkeit des Betons
Druckspannung im Stahl
Die Betonverkürzung unter zentrischem Druck ist beim σ-ε-Parabel-Rechteck-Diagramm auf εc2 begrenzt. Durch den Verbund von Beton und Stahl sind die Verkürzungen für den Bewehrungsstahl identisch und wir können auf dessen Spannung schließen.
| σs | Spannung in Bewehrung |
| fyd | Bemessungswert der Streckgrenze von Bewehrungsstahl = fyk / γs |
| εc2 | relative Druckverformung bei maximaler Spannung |
| Es | Elastizitätsmodul |
| fyk | charakteristische Streckgrenze |
| γs | Teilsicherheitsbeiwert des Stahls |
| εud | Bemessungsgrenzverformung = fyd / Es |
Druckspannung im Beton
Betonspannung
fcd = αcc ⋅ fck / γc
αcc ... Beiwert zur Berücksichtigung von Langzeiteinwirkungen auf Druckfestigkeit
fck ... charakteristische Druckfestigkeit des Betons
γc ... Teilsicherheitsbeiwert bezogen auf Beton
Abmessungen des Betonquerschnitts
Die Kraft, die durch den Betonquerschnitt ausgeglichen werden kann, entspricht seiner maximalen Drucktragfähigkeit, die direkt von seinem Querschnitt und seiner Beanspruchbarkeit abhängt.
Ausgleichskraft des Betons
Fc = Ac ⋅ fcd
Die Bewehrung gleicht also den Rest der zentrischen Drucklast aus.
Ausgleichskraft der Bewehrung
Fs = NEd - Fc
Aus diesen beiden Gleichgewichtsgleichungen kann auf den zu bemessenden Betonquerschnitt und dann auf den der Bewehrung geschlossen werden.
Betonquerschnittsfläche
Ac ≥ NEd / (fcd + As / Ac ⋅ σs)
As = Fs/σs ... Querschnittsfläche der Bewehrung
Anwendung der Theorie mit dem Zusatzmodul RF-BETON Stäbe
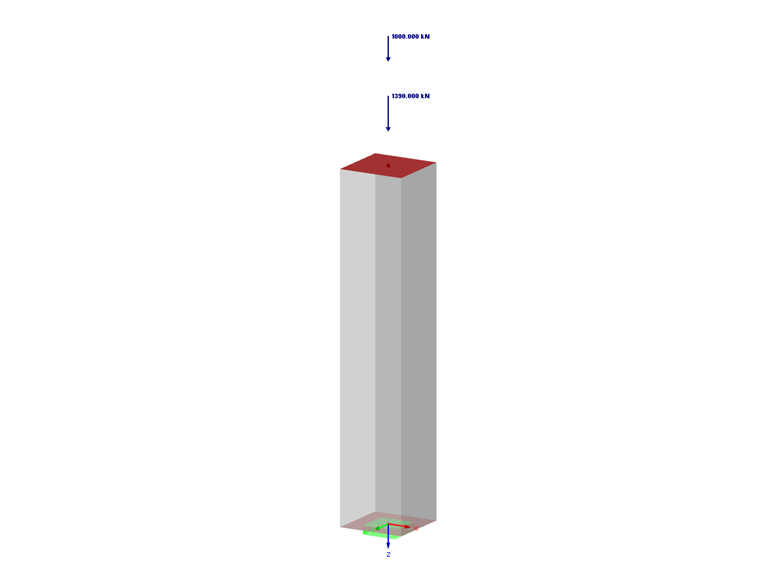
Es werden nun die Ergebnisse untersucht, die wir automatisch bei der Berechnung der Bewehrung erhalten haben. Da auch der zu bemessende Betonquerschnitt ermittelt werden soll, hat das RFEM 5-Basismodell eine definierte Breite sowie eine unbekannte Höhe, die größer oder gleich der Breite ist.
Wir betrachten folgende Parameter:
- Ständige Lasten: Ng = 1390 kN
- Veränderliche Lasten: Nq = 1000 kN
- Stützenlänge: l = 2,1 m
- Zu bestimmender Rechteckquerschnitt: Breite b = 40 cm / unbekannte Höhe ≥ 40 cm
- Das Eigengewicht der Stütze ist vernachlässigbar.
- Stütze nicht in Aussteifungsverband integriert.
- Betonfestigkeitsklasse: C25/30
- Stahl: S 500 A bei ansteigendem Ast
- Durchmesser der Längsbewehrung: ϕ = 20 mm
- Durchmesser der Querbewehrung: ϕt = 8 mm
- Betondeckung: 3 cm
Materialkennwerte
Bemessungswert der Druckfestigkeit des Betons
fcd = 1 ⋅ 25 / 1,5 = 16,7 MPa
Relative Druckverformung bei maximaler Spannung
εc2= 2 ‰
Bemessungswert der Streckgrenze von Bewehrungsstahl
fyd = 500 / 1,15 = 435 MPa
Grenzverformung in Bewehrung
εud = fyd / Es = 435 / (2 ⋅ 105) = 2,17 ‰
Spannung in Bewehrung
σs = 2 ⋅ 105 ⋅ 0,002 = 400 MPa car εc2 < εud
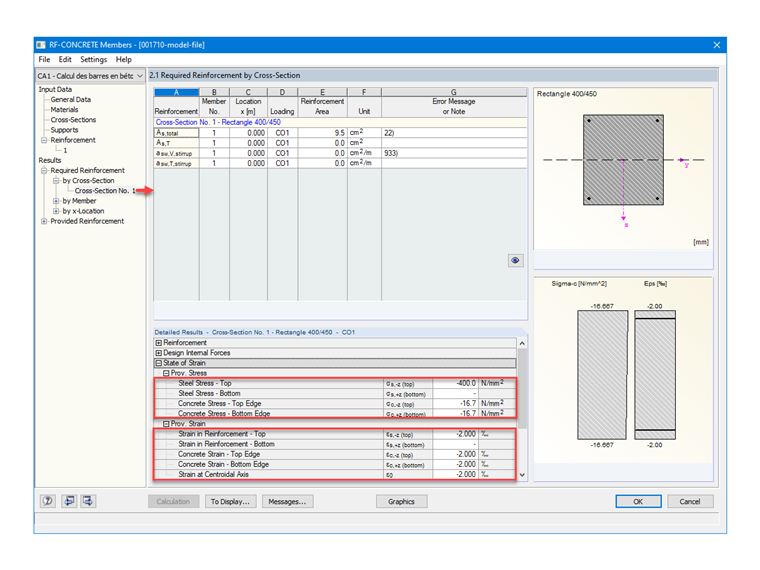
Zur Überprüfung der Materialeinstellungen in RF-BETON Stäbe sind in Bild 02 die vorhandenen Spannungen und Dehnungen für Beton und die erforderliche Bewehrung dargestellt.
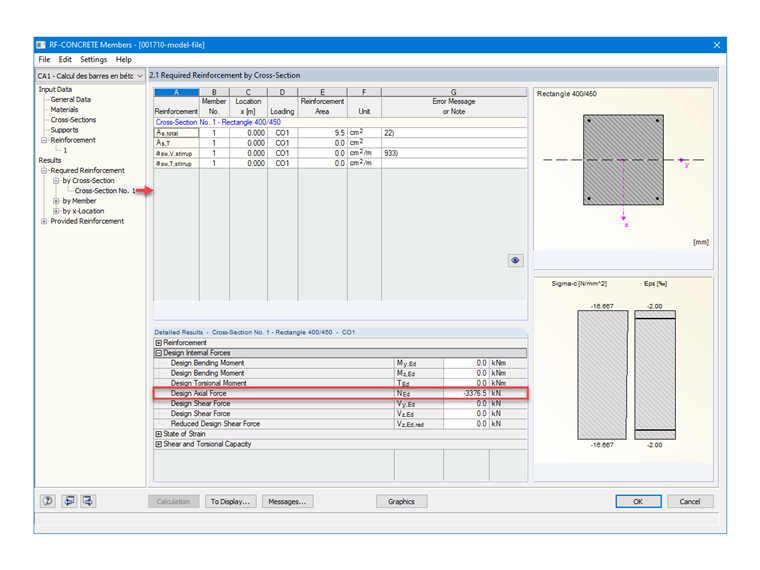
´État Grenzzustand der Tragfähigkeit
Beanspruchungen im Grenzzustand der Tragfähigkeit
NEd = 1,35 ⋅ Ng + 1,5 ⋅ Nq
NEd = 1,35 ⋅ 1390 + 1,5 ⋅ 1000 = 3,38 MN
Auswirkungen nach Theorie II. Ordnung sind im GZT nicht berücksichtigt.
Um die Last korrekt am Kopf der Stütze ansetzen zu können, haben wir in unserem Modell einen Stab modelliert, der nur am Fuß eingespannt und am Kopf frei ist. Wir möchten jedoch berücksichtigen, dass der Stützenkopf an Trägern befestigt ist, wobei davon ausgegangen wird, dass die Stütze weniger steif ist als die Träger. Wir können somit davon ausgehen, dass der Stab an beiden Enden eingespannt ist. Theoretisch sollten also die Biegsamkeitsbeiwerte für eine perfekte Einspannung null sein. In der Praxis gibt es jedoch keine perfekten Einspannungen. Der für die Biegsamkeitsbeiwerte zu berücksichtigende Mindestwert ist daher: k1 ou k2 = 0,1.
Knicklängenbeiwert
kcr = 0,5 ⋅ (1 + 0,1 / (0,45 + 0,1)) = 0,59
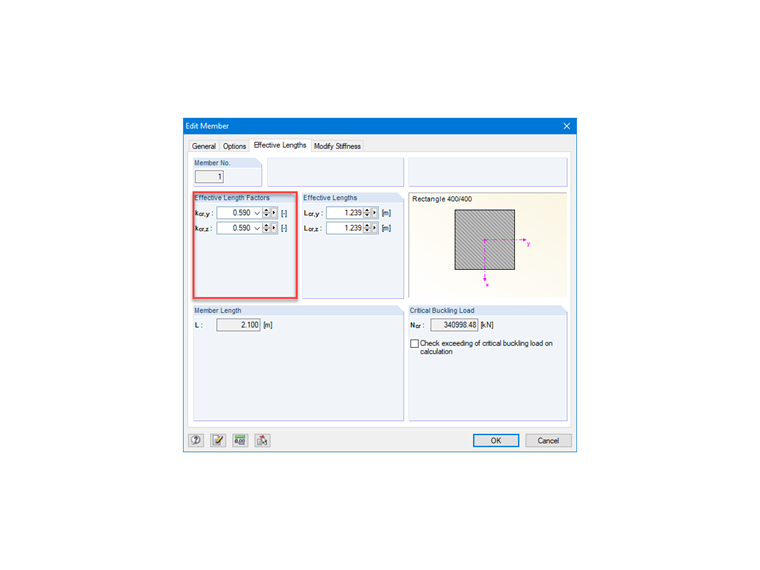
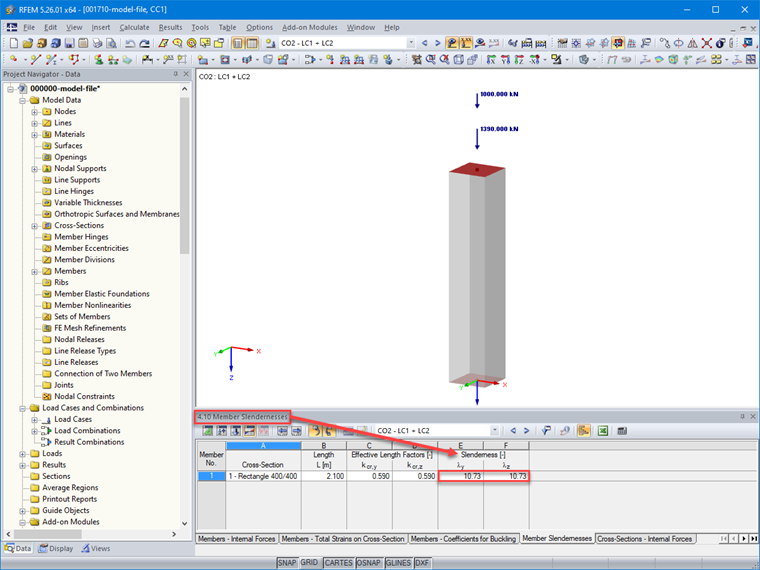
Bild 04 zeigt die Möglichkeit, den Knicklängenbeiwert für das Stabelement in RFEM einzustellen.
Da die Querschnittshöhe ermittelt werden muss, wird davon ausgegangen, dass h > b und so der Trägheitsradius eines rechteckigen Querschnitts für die geringe Breite maßgebender ist.
Maßgebender Trägheitsradius in der Ebene parallel zur Breite b = 40 cm
iz = b / √12
Schlankheit
λz = (0,59 ⋅ 2,1 ⋅ √12) / 0,40 = 10,73 m
Bild 05 zeigt die Schlankheitswerte in der RFEM-Tabelle 4.10, die für den Stab nach der Berechnung ermittelt wurden.
Zur Kontrolle der Schlankheit bestimmen wir manuell die Grenzschlankheit unter der Annahme von h = b.
Grenzschlankheit
n = 3,38 / (0,40² ⋅ 16,7) = 1,26
λlim = 20 ⋅ 0,7 ⋅ 1,1 ⋅ 0,7 / √1,26 = 9,6 m
λz > λlim → Die Bedingung ist nicht erfüllt.
Wir werden jedoch trotzdem mit zentrischem Druck rechnen, da wir im Hinblick auf die geringe Abweichung sogleich feststellen, dass mit der Ermittlung der tatsächlichen Querschnittshöhe nämlich die Bedingung erfüllt wird.
Die zu berechnende tatsächliche Höhe
Um die reale Höhe h des Querschnitts zu ermitteln, kann für den zu berücksichtigenden Bewehrungsgrad von folgender Annahme ausgegangen werden: As/Ac = 1 %. Nun können wir auf den zu berechnenden tatsächlichen Querschnitt und dessen Höhe entsprechend der Spannung in der Bewehrung und der Querschnittsbreite b schließen.
Betonquerschnittsfläche
Ac ≥ 3,38 / (16,7 + 400 / 100) = 0,163 m²
Profilhöhe
Ac = b ⋅ h → h ≥ 0,163 / 0,4 = 0,41 m
Die Annahme h > b für die Berechnung der Schlankheit ist korrekt, und wir können eine Querschnittshöhe auswählen, indem wir ein Vielfaches von 5 cm wählen, also h = 45 cm.
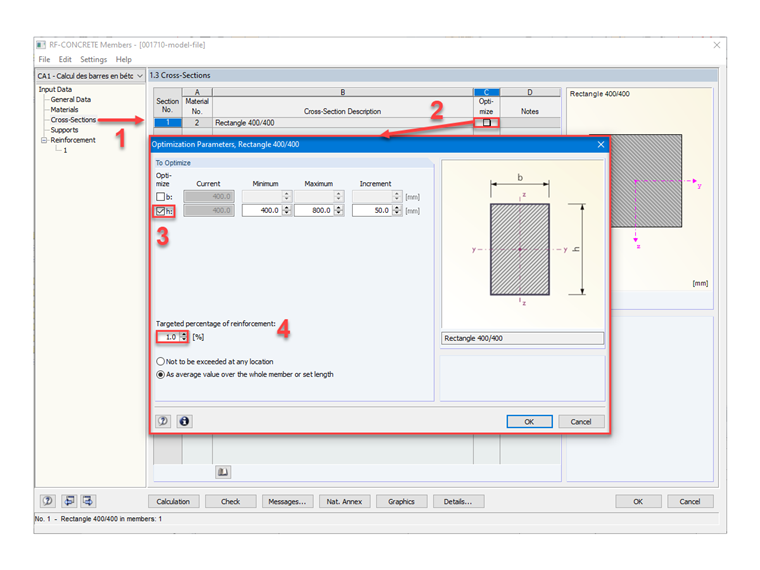
Bild 06 zeigt die Schritte zur automatischen Ermittlung der Höhe des Rechteckquerschnitts in RF-BETON Stäbe mithilfe der Funktion "Optimieren".
Tragfähiger Querschnitt
Ausgleichskraft des Betons
Fc = 0,40 ⋅ 0,45 ⋅ 16,7 = 3 MN
Ausgleichskraft der Bewehrung
Fs= 3,376 - 3 = 0,38 MN
Wir leiten den entsprechenden Bewehrungsquerschnitt ab:
Fläche des Bewehrungsquerschnitts
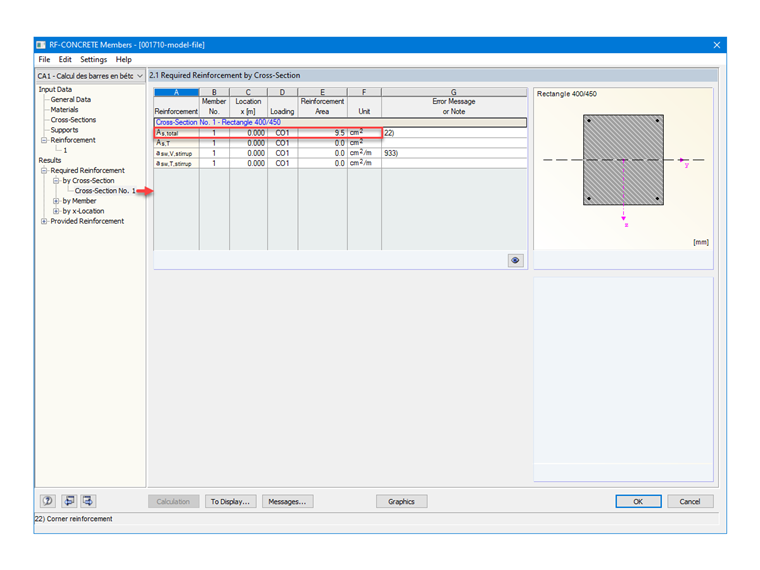
As = 0,38 / 400 ⋅ 104 = 9,5 cm²
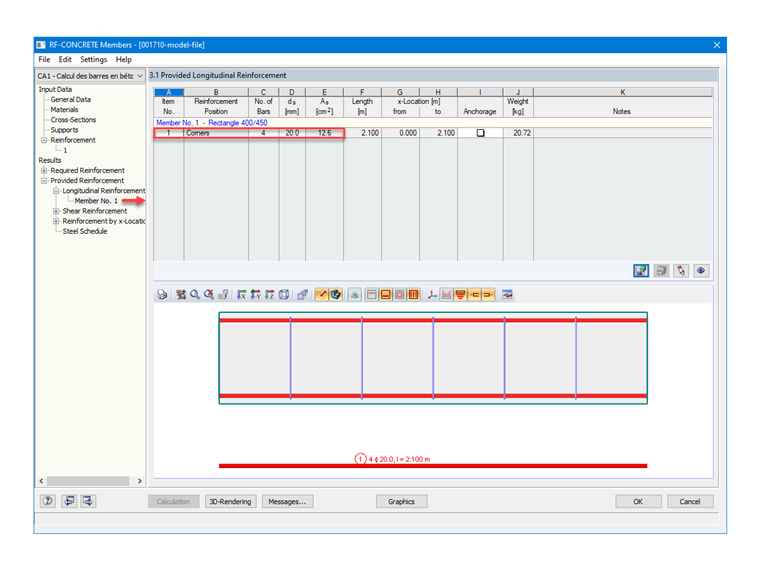
Da wir den Bewehrungsstahl in RF-BETON Stäbe mit einem Durchmesser von 20 mm eingestellt haben, ergibt sich eine vom Zusatzmodul automatisch ermittelte vorhandene Bewehrung von 4 Stäben mit einer Verteilung in den Ecken wie gewünscht, d.h. 1 HA 20 pro Ecke. Daraus ergibt sich folgende Bewehrungsquerschnittsfläche:
As = 4 ⋅ 3,142 = 12,57 cm²
Mechanischer Bewehrungsgrad
ω = (As ⋅ fyd) / (Ac ⋅ fcd) = 12,57 ⋅ 435 / (40 ⋅ 45 ⋅ 16,7) = 0,182
Abschlussnachweis der Grenzschlankheit weil h > b
n = 3,38 / (0,40 ⋅ 0,45 ⋅ 16,7) = 1,125
B = √(1 + 2 ⋅ ω) = 1,17
λlim = 20 ⋅ 0,7 ⋅ 1,17 ⋅ 0,7 / √1,125 = 10,81 m
λz < λlim → Das Schlankheitskriterium ist erfüllt.
Anwendung in anderen Zusatzmodulen
Mit dem Zusatzmodul RF-BETON Stützen kann auch die Bewehrung für ein Element unter zentrischem Druck ermittelt werden. Einen Fachbeitrag zum Vergleich mit RF-BETON Stäbe finden Sie hier:
