Co je namáhání v osovém tlaku?
Průřez konstrukčního prvku je namáhán v osovém tlaku, pokud se síly působící na jednu stranu průřezu redukují v těžišti průřezu na jedinou sílu N. Tato normálová síla N je tedy kolmá k průřezu a směřuje k němu. Na rozdíl od kombinovaného ohybu se toto namáhání v praxi nikdy nevyskytuje, protože skutečný sloup je vždy vystaven buď asymetrii zatížení nebo imperfekcím v konstrukci sloupu, jak je vidět v tomto odborném příspěvku:
Štíhlostní kritérium pro osamělé prvky
Vychází se z toho, že účinky druhého řádu (imperfekce, asymetrie atd.) lze zanedbat, pokud je prvek namáhán pouze osově v tlaku silou NEd a pokud je splněno kritérium štíhlosti.
Štíhlostní kritérium
λ < λlim
λ ... součinitel štíhlosti
λlim ... Mezní štíhlost
Štíhlost a účinná délka podle EN 1992-1-1
| λ | štíhlostní poměr |
| l0 | účinná délka = kcr ⋅ l |
| i | poloměr setrvačnosti betonového průřezu bez trhlin |
| kcr | součinitel vzpěrné délky = 0,5 ⋅ √[(1 + k1 / (0,45 + k1)) ⋅ (1 + k2 / (0,45 + k2))] podle 5.8.3.2(3), rovnice (5.15) |
| l | volná délka |
| k1, k2 | poměrné poddajnosti na obou koncích prvku |
Mezní štíhlost podle EN 1992-1-1
Mezní štíhlost
λlim = (20 ⋅ A ⋅ B ⋅ C) / √n podle 5.8.3.1(1), rovnice (5.13N)
A = 1 / (1 + 0,2 φef) = 0,7, neznáme-li φef
B = √ (1 + 2 ⋅ ω) = 1,1, neznáme-li ω
C = 1,7 - rm = 0,7, neznáme-li rm
n = NEd/(Ac ⋅ fcd ) ... relativní normálová síla
φef ... Účinný součinitel dotvarování
ω ... Mechanický stupeň vyztužení
rm ... Poměr momentů
NEd ... Návrhová hodnota působící normálové síly
Ac ... Celková plocha betonového průřezu
fcd ... Návrhová hodnota pevnosti betonu v tlaku
Tlakové napětí v oceli
Zkrácení betonu při osovém tlaku je v případě parabolicko-rektangulárního pracovního diagramu σ-ε omezeno hodnotou εc2. Vzhledem k soudržnosti mezi betonem a ocelí jsou zkrácení u ocelové výztuže stejná a lze z nich odvodit napětí.
| σs | napětí ve výztuži |
| fyd | návrhová mez kluzu betonářské výztuže = fyk / γs |
| εc2 | poměrné přetvoření v tlaku při dosažení maximálního napětí |
| Es | modul pružnosti |
| fyk | charakteristická mez kluzu |
| γs | dílčí součinitel betonářské oceli |
| εud | návrhové mezní přetvoření = fyd / Es |
Tlakové napětí v betonu
Napětí v betonu
fcd = αcc ⋅ fck / γc
αcc ... Součinitel zohledňující dlouhodobé účinky na pevnost v tlaku
fck ... Charakteristická pevnost betonu v tlaku
γc ... Dílčí součinitel pro beton
Rozměry betonového průřezu
Síla, kterou může vyvažovat betonový průřez, odpovídá jeho maximální únosnosti v tlaku, která přímo závisí na jeho průřezu a návrhové pevnosti.
Vyrovnávací síla betonu
Fc = Ac ⋅ fcd
Výztuž pak vyvažuje zbytek zatížení v osovém tlaku.
Vyrovnávací síla výztuže
Fs = NEd - Fc
Z těchto dvou rovnic rovnováhy lze odvodit průřez betonu a následně také výztuže.
Plocha betonového průřezu
Ac ≥ NEd / (fcd + As / Ac ⋅ σs)
As = Fs/σs ... Průřezová plocha výztuže
Uplatnění teorie pomocí přídavného modulu RF-CONCRETE Members
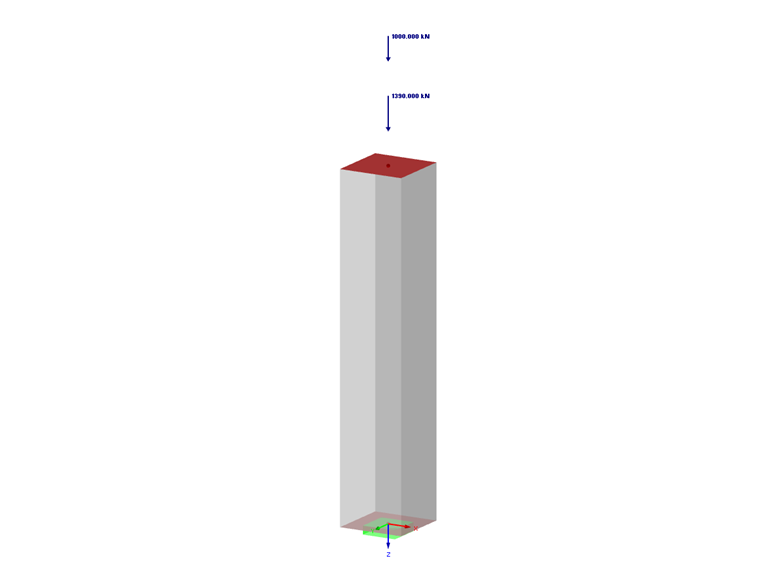
Nyní přistoupíme k analýze výsledků, které jsme automaticky obdrželi při výpočtu výztuže. Protože je třeba také stanovit průřez betonu k posouzení, bude mít základní model v programu RFEM 5 definovanou šířku a neznámou výšku, která je větší nebo rovna šířce.
Budeme uvažovat následující parametry:
- Stálá zatížení: Ng = 1390 kN
- Proměnná zatížení: Nq = 1 000 kN
- Délka sloupu: l = 2,1 m
- Obdélníkový průřez ke stanovení: šířka b = 40 cm / neznámá výška ≥ 40 cm
- Vlastní tíhu sloupu lze zanedbat.
- Sloup není součástí ztužení.
- Třída pevnosti betonu: C25/30
- Ocel: S 500 A se stoupající větví
- Průměr podélné výztuže: ϕ = 20 mm
- Průměr příčné výztuže: ϕt = 8 mm
- Krycí betonová vrstva: 3 cm
Materiálové charakteristiky
Návrhová hodnota pevnosti betonu v tlaku
fcd = 1 ⋅ 25 / 1,5 = 16,7 MPa
Poměrné přetvoření v tlaku při maximálním napětí
εc2= 2‰
Návrhová mez kluzu betonářské oceli
fyd = 500 / 1,15 = 435 MPa
Mezní přetvoření ve výztuži
εud = fyd / Es = 435 / (2 ⋅ 105) = 2,17‰
Napětí ve výztuži
σs = 2 ⋅ 105 ⋅ 0,002 = 400 MPa neboť εc2 < εud
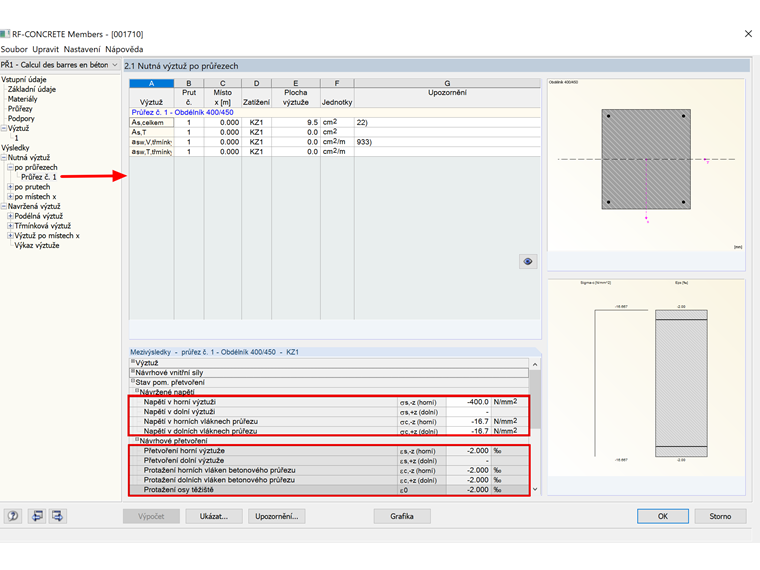
Pro kontrolu nastavení materiálu v modulu RF-CONCRETE Columns jsou na obrázku 2 znázorněna návrhová napětí a přetvoření u betonu a nutné výztuže.
´État Mezní stav únosnosti
Namáhání v mezním stavu únosnosti
NEd = 1,35 ⋅ Ng + 1,5 ⋅ Nq
NEd = 1,35 ⋅ 1390 + 1,5 ⋅ 1000 = 3,38 MN
Účinky druhého řádu se v MSÚ nezohledňují.
Pro správné zohlednění zatížení v hlavě sloupu jsme v našem modelu namodelovali prut, který je vetknutý pouze v patě a v hlavě je volný. Chceme ovšem vzít v úvahu, že sloup je v hlavě připevněn k nosníkům, a vychází se z toho, že sloup má menší tuhost než nosníky. Lze tak uvažovat vetknutí prutu na jeho obou koncích. Proto by teoreticky měly být součinitele poddajnosti pro dokonalé vetknutí nulové. V praxi ovšem neexistuje dokonalé vetknutí. Minimální hodnota, která se má zohlednit u součinitelů poddajnosti, je proto: k1 nebo k2 = 0,1.
Součinitel vzpěrné délky
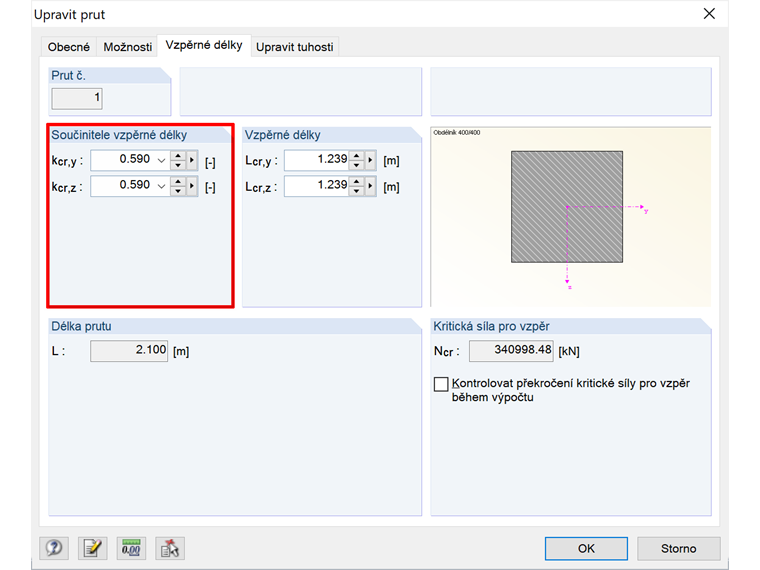
kcr = 0,5 ⋅ (1 + 0,1 / (0,45 + 0,1)) = 0,59
Na obrázku 4 vidíme možnost nastavení součinitele vzpěrné délky u prutového prvku v programu RFEM.
Protože výšku průřezu je třeba určit, vychází se z toho, že h > b, a pro malou šířku je tedy poloměr setrvačnosti obdélníkového průřezu rozhodující.
Stanovení poloměru rozhodující setrvačnosti v rovině rovnoběžné s šířkou b = 40 cm
iz = b / √12
Štíhlosti
λz = (0,59 ⋅ 2,1 ⋅ √12) / 0,40 = 10,73 m
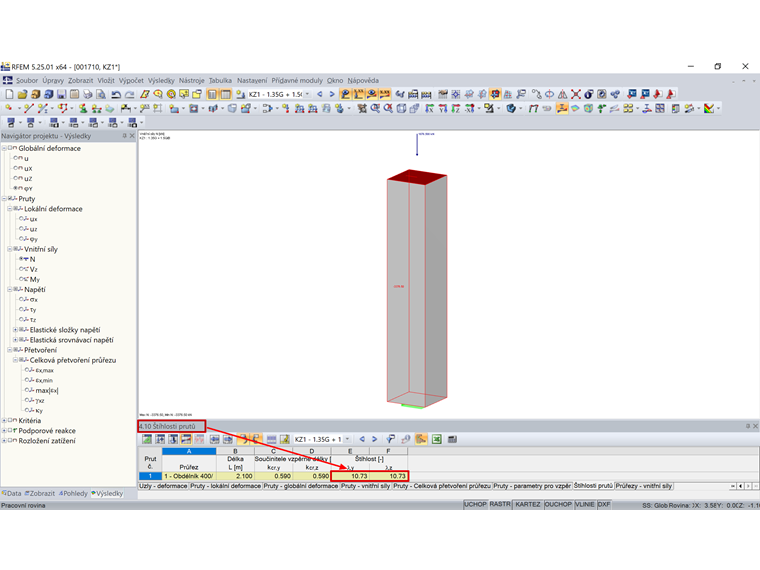
Na obr. 05 se uvádí hodnoty štíhlosti pro prut v tabulce 4.10 v programu RFEM po skončení výpočtu.
Pro kontrolu štíhlosti stanovíme ručně mezní štíhlost za předpokladu h = b.
Mezní štíhlost
n = 3,38 / (0,40² ⋅ 16,7) = 1,26
λlim = 20 ⋅ 0,7 ⋅ 1,1 ⋅ 0,7 / √1,26 = 9,6 m
λz > λlim → Podmínka není splněna.
Nicméně budeme přesto počítat s osovým tlakem, protože s ohledem na malou odchylku pak zjistíme, že při stanovení skutečné výšky průřezu bude podmínka splněna.
Skutečná výška pro výpočet
Pro stanovení skutečné výšky h průřezu lze u stupně vyztužení vycházet z následujícího předpokladu: As/Ac = 1%. Z napětí ve výztuži a šířky průřezu b pak můžeme odvodit skutečný posuzovaný průřez a jeho výšku.
Plocha betonového průřezu
Ac ≥ 3,38 / (16,7 + 400 / 100) = 0,163 m²
Výška průřezu
Ac = b ⋅ h → h ≥ 0,163 / 0,4 = 0,41 m
Předpoklad h > b pro výpočet štíhlosti je správný a můžeme zvolit výšku průřezu, která je násobkem 5 cm, tedy h = 45 cm.
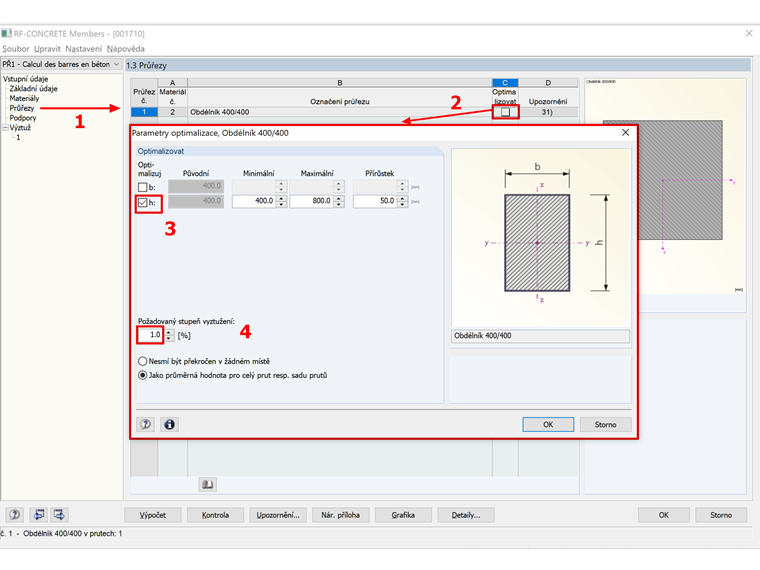
Na obrázku 6 jsou popsány kroky pro automatické stanovení výšky obdélníkového průřezu v modulu RF-CONCRETE Members pomocí funkce „Optimalizovat“.
Zatížený průřez
Vyrovnávací síla betonu
Fc = 0,40 ⋅ 0,45 ⋅ 16,7 = 3 MN
Vyrovnávací síla výztuže
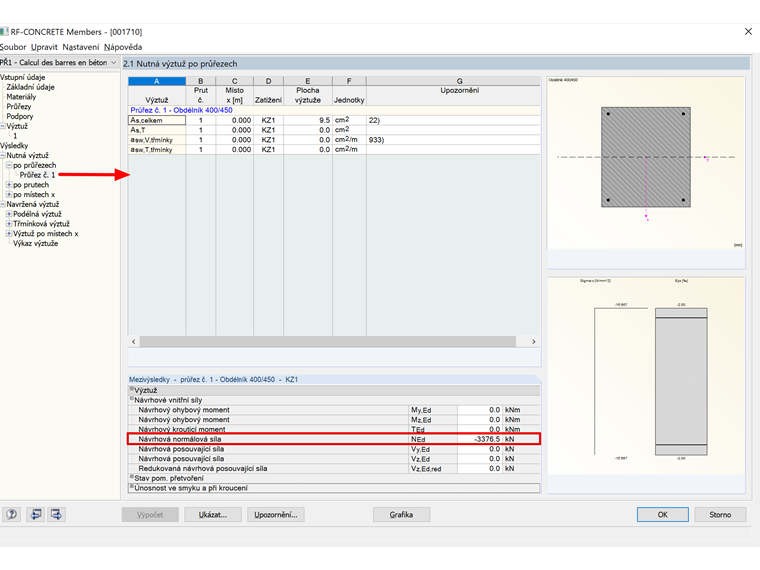
Fs= 3,376 - 3 = 0,38 MN
Odvodíme příslušný průřez výztuže:
Průřezová plocha výztuže
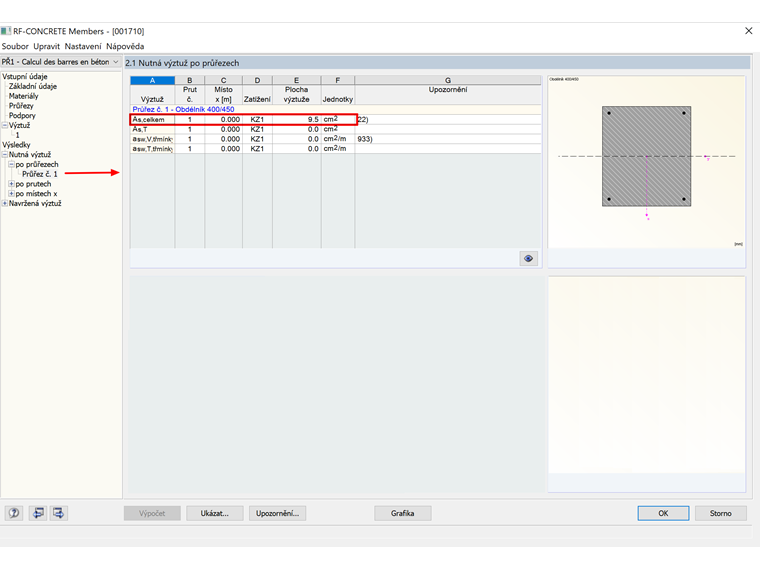
As = 0,38 / 400 ⋅ 104 = 9,5 cm²
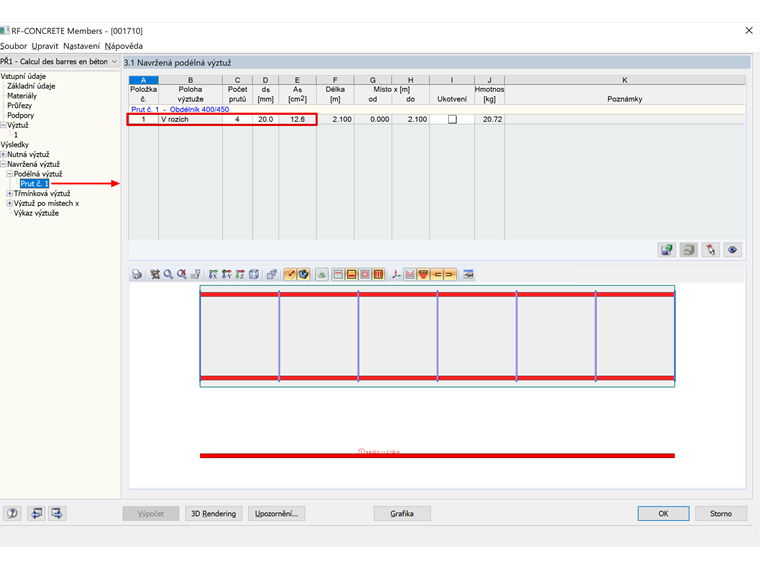
Protože jsme v modulu RF-CONCRETE Members nastavili betonářskou výztuž o průměru 20 mm, stanoví modul automaticky 4 pruty návrhové výztuže s rozmístěním v rozích, tj. 1 HA 20 na roh. Výsledkem je tedy průřezová plocha a následující:
As = 4 ⋅ 3,142 = 12,57 cm²
Mechanický stupeň vyztužení
ω = (As ⋅ fyd )/(Ac ⋅ fcd ) = 12,57 ⋅ 435/(40 ⋅ 45 ⋅ 16,7) = 0,182
Závěrečná kontrola mezní štíhlosti, protože h > b
n = 3,38/(0,40 ⋅ 0,45 ⋅ 16,7) = 1,125
B = √ (1 + 2 ⋅ ω) = 1,17
λlim = 20 ⋅ 0,7 ⋅ 1,17 ⋅ 0,7/√1,125 = 10,81 m
λz < λlim → Štíhlostní kritérium je splněno.
Použití v jiných přídavných modulech
Modul RF-CONCRETE Columns také umožňuje stanovit výztuž pro prvek namáhaný v osovém tlaku. Odborný článek o rozdílech mezi RF-CONCRETE Members a RF-CONCRETE Columns najdete zde:
