在线手册 RFEM 6 基础知识

返回在线手册

540x

004088

2023-09-28

选择手册

概览

简介

计算

有限单元

材料非线性

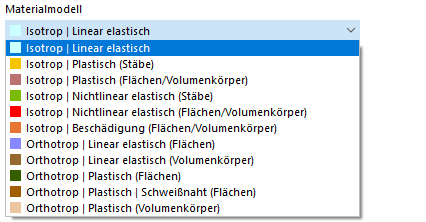
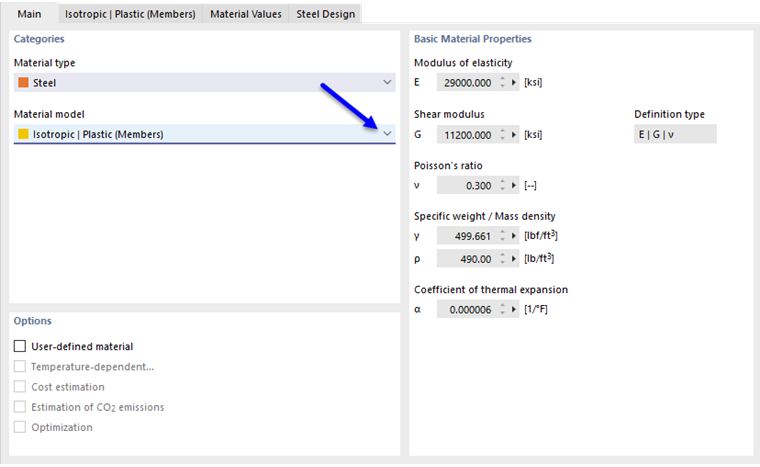
如果在模型 - 基础数据中激活了非线性材料行为分析插件（需要许可证），在材料模型列表中，除了"各向同性 | 线性弹性"和"正交各向异性 | 线性弹性"材料模型之外，还可以选择其他选项。

“非线性材料行为”分析模块材料模型

如果在RFEM中使用非线性材料模型，始终会进行迭代计算。根据材料模型，定义了不同的应力-应变关系。

在迭代过程中，无限元的刚度不断调整，直到满足应力-应变关系。调整始终是针对整个表面或实心元素进行的。因此，我们建议在评估应力时，总是使用网格元素上的"常数"平滑类型。

结果平滑

在RFEM中的一些材料模型以"塑性"表示，另一些以"非线性弹性"表示。

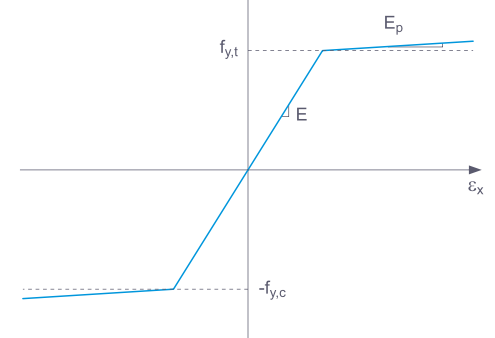
如果对一个非线性弹性材料的结构构件再次释放，应变将沿同一路径返回。在完全卸载时，不会留有应变。

应力-应变图，非线性弹性

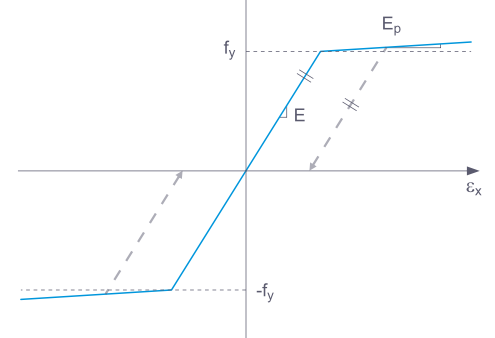
当卸载一个采用塑性材料模型的结构构件时，完全卸载后仍然会残留应变。

应力-应变图，塑性

关于非线性材料模型的背景信息可以在描述各向同性非线性弹性材料模型的屈服法则的技术文章中找到。

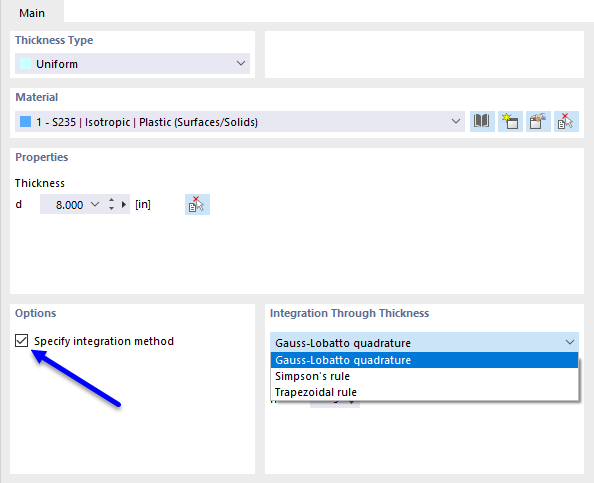
在具有非线性材料的板中的内力和弯矩是由板厚度d上的应力数值积分得出的。要定义厚度的积分方法，请在“编辑厚度”对话框中选择指定积分方法选项。可用的积分方法有：

高斯-洛巴托求积法
辛普森法则
梯形法则

定义面厚度的积分方法

此外，你可以根据板厚度从3到99之间指定“积分点的数量”。

信息

有关各个积分方法的理论解释，请参见多层表面在线手册。

各向同性塑性 | 梁段)

选择“材料模型”下拉列表中的各向同性 | 塑性(梁段)条目时，会启用用于输入非线性材料参数的选项卡。

激活非线性材料模型

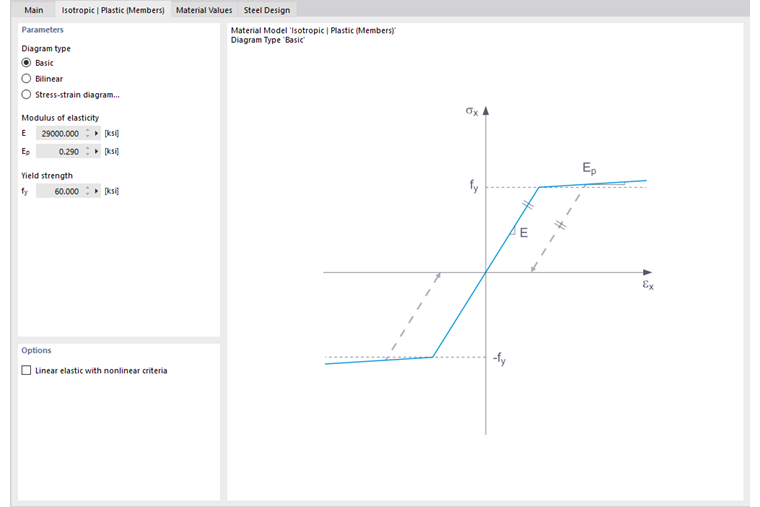
定义非线性材料参数

在此选项卡中，你定义应力-应变图。可用的选项有：

基本
双线性
应力-应变图

如果选择了基本，RFEM使用双线性材料模型。弹性模量E和屈服强度f_y的值来自材料数据库。出于数值原因，图表的分支不完全水平，而是具有一个小的E_p斜率。

如果你想更改屈服强度和弹性模量的值，请在“主”选项卡中激活“用户定义材料”复选框。

激活用户自定义材料

对于双线性定义，你还可以输入E_p的值。

通过“应力-应变图”可以定义应力与应变之间的更复杂关系。选择此选项时，将显示“应力-应变图”选项卡。

输入用户自定义的应力-应变图

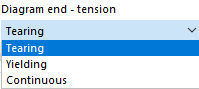
在每个表格行中为应力-应变关系定义一个点。你可以选择图形在最后一个定义点后的继续方式，在图形下的“图表结束”列表中进行选择：

最后一个定义点之后的曲线变化

在“撕裂”的情况下，最后一个定义点之后的应力跳回到零。“屈服”意味着应变增加时应力保持不变。“连续”意味着图形继续沿最后一段的斜率延伸。

信息

在此材料模型中，应力-应变图是指纵向应力σ_x。该材料模型无法考虑不同的拉伸和压缩屈服强度。

各向同性塑性 | 表面/实体

选择“材料模型”下拉列表中的“各向同性 | 塑性(表面/实体)”条目时，会启用用于输入非线性材料参数的选项卡。

选择塑性材料模型

首先，选择“应力失效假设”。可供选择的假设有：

冯·米塞斯 (冯·米塞斯屈服准则)
Tresca (Tresca屈服准则)
Drucker-Prager
Mohr-Coulomb

定义应力破坏假设

选择“冯·米塞斯”时，应力-应变图中使用以下应力：

表面：

σ_{v} = \sqrt{σ_{x}^{2} + σ_{y}^{2} - σ_{x} σ_{y} + 3 (τ_{xy}^{2})}

根据 von Mises 由基本应力计算等效应力

实体：

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

根据基本应力计算等效应力 σ_v,Mises

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

由主应力计算的等效应力 σ_v,Mises

根据“特雷斯卡”假设，使用以下应力：

表面：

σ_{v} = \sqrt{{(σ_{x} - σ_{y})}^{2} + 4 {τ_{xy}}^{2}}

根据 Tresca 的等效应力

实体：

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

等效应力 σ_v,Tresca

根据“德鲁克-普拉格”假设，对于表面和实体使用以下应力：

σ_{v} = \frac{m - 1}{2} (σ_{1} + σ_{2} + σ_{3}) + \frac{m + 1}{2} \sqrt{\frac{1}{2} [{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}]}

m = \frac{σ_{c}}{σ_{t}}

σ_c	压力极限应力
σ_t	拉应力的极限

Drucker-Prager 屈服准则

根据“莫尔-库仑”假设，对于表面和实体使用以下应力：

σ_{v} = \frac{m + 1}{2} \max \{|σ_{1} - σ_{2}| + K (σ_{1} + σ_{2}), |σ_{2} - σ_{3}| + K (σ_{2} + σ_{3}), |σ_{3} - σ_{1}| + K (σ_{3} + σ_{1})\}

K = \frac{m - 1}{m + 1}

m = \frac{σ_{c}}{σ_{t}}

莫尔-库伦

各向同性非线性弹性 | 梁段

其功能大体上与各向同性塑性（梁段）材料模型相似。不同之处在于卸载后没有塑性应变残留。

各向同性非线性弹性 | 表面/实体

其功能大体上与各向同性塑性（表面/实体）材料模型相似。不同之处在于卸载后没有塑性应变残留。

各向同性损伤 | 表面/实体

与其他材料模型不同，该材料模型的应力-应变图对于原点不是反对称的。因此，例如可以用此材料模型表示钢纤维增强混凝土的行为。有关钢纤维增强混凝土建模的详细信息，请参阅钢纤维增强混凝土材料属性的确定的技术文章。

材料模型“各向同性” | 损伤"

在此材料模型中，各向同性刚度随着标量损伤参数的变化而降低。该损伤参数是从图表中定义的应力曲线中确定的。该模型不考虑主应力的方向；相反，损伤在等效应变的方向上发生，同时也涵盖了垂直于平面的第三方向。应力张量的拉伸和压缩区域分开处理，在每种情况下适用不同的损伤参数。

"参考元素尺寸"控制裂缝区域中应变相对于元素长度的缩放。默认值为零时，不进行缩放。因此，钢纤维增强混凝土的材料行为被真实地建模。

有关“各向同性损伤”材料模型的理论背景的更多信息，请参阅描述非线性材料模型损伤的技术文章。

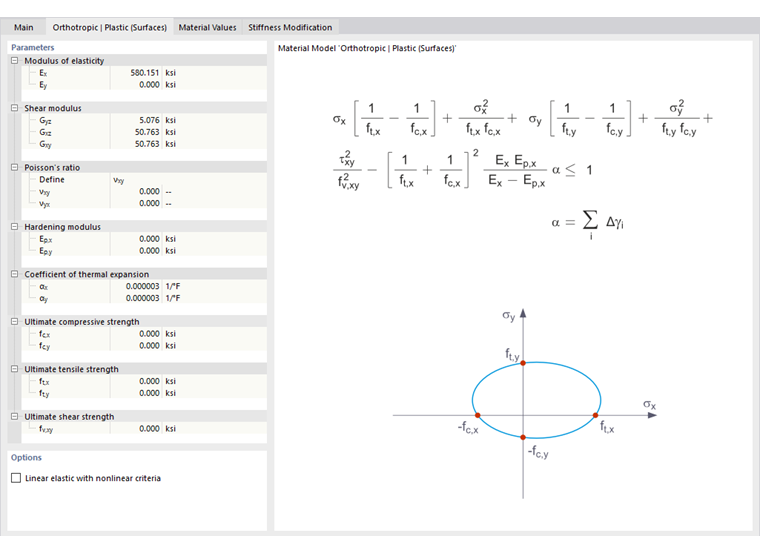
正交各向异性塑性 | 表面/实体

根据“蔡-吴”理论的材料模型将塑性与正交各向异性的性质结合起来。这允许对具有各向异性特征的材料如纤维增强塑料或木材进行特殊建模。

如果材料发生塑性变形，应力保持不变。根据各个方向上可用的刚度进行再分配。

材料模型“正交各向异性” | 塑性（面）"

材料模型 ' 正交各向异性 | 塑料（实体）'

弹性区域对应正交各向异性材料模型。蔡-吴屈服条件在塑性区适用：

表面(2D):

σ_{x} [\frac{1}{f_{t, x}} - \frac{1}{f_{c, x}}] + \frac{{σ_{x}}^{2}}{f_{t, x} f_{c, x}} +

σ_{y} [\frac{1}{f_{t, y}} - \frac{1}{f_{c, y}}] + \frac{{σ_{y}}^{2}}{f_{t, y} f_{c, y}} +

\frac{{τ_{xy}}^{2}}{{f_{v, xy}}^{2}} - {[\frac{1}{f_{t, x}} + \frac{1}{f_{c, x}}]}^{2} \frac{E_{x} E_{p, x}}{E_{x} - E_{p, x}} α \leq 1

α = \sum_{i} ∆ γ_{i}

Tsai-Wu，平面应力状态

实体(3D):

σ_{x} [\frac{1}{f_{t, x}} - \frac{1}{f_{c, x}}] + \frac{{σ_{x}}^{2}}{f_{t, x} f_{c, x}} +

σ_{y} [\frac{1}{f_{t, y}} - \frac{1}{f_{c, y}}] + \frac{{σ_{y}}^{2}}{f_{t, y} f_{c, y}} +

σ_{z} [\frac{1}{f_{t, z}} - \frac{1}{f_{c, z}}] + \frac{{σ_{z}}^{2}}{f_{t, z} f_{c, z}} +

\frac{{τ_{yz}}^{2}}{{f_{v, yz}}^{2}} + \frac{{τ_{xz}}^{2}}{{f_{v, xz}}^{2}} + \frac{{τ_{xy}}^{2}}{{f_{v, xy}}^{2}} -

{[\frac{1}{f_{t, x}} + \frac{1}{f_{c, x}}]}^{2} \frac{E_{x} E_{p, x}}{E_{x} - E_{p, x}} α \leq 1

α = \sum_{i} ∆ γ_{i}

Tsai-Wu，应力空间状态

所有强度必须定义为正值。

你可以将应力准则视为六维应力空间中的椭球面。如果将三种应力组件中的一种作为常数值应用，可以将该表面投影到三维应力空间。

如果根据蔡-吴方程的面内应力条件f_y(σ)小于1，应力在弹性区。当f_y(σ) = 1时达到塑性区。不允许超过1的值。模型行为是理想塑性的，这意味着没有强化。

上级章节

非线性