VE0067 | 不可压缩材料 - 厚壁容器

项目介绍

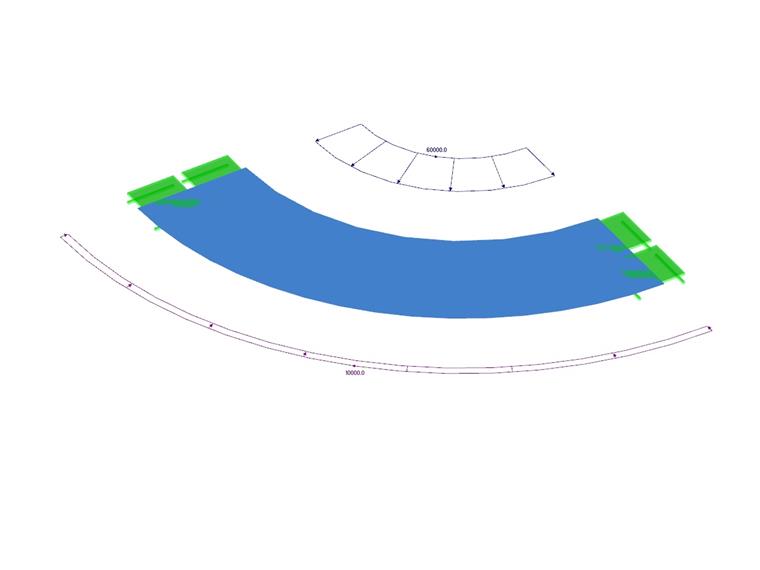
该验算示例是 VE0064 - 厚壁容器的验算示例，唯一的区别是容器的材料是不可压缩的。厚壁容器受到内部压力和外部压力。容器底部为开口设计，不产生正应力。该问题采用四分之一模型建模，并通过以下参数集进行描述。不考虑自重的情况下，通过内外半径 u_r (r₁ ) ，u_r (r₂ ) 计算径向挠度。

材料	弹性的不可压缩的	弹性模量	E	1.000	MPa
材料	弹性的不可压缩的	泊松比	ν	0.499	-
几何尺寸		内弧半径	r₁	200.000	毫米
几何尺寸		外部半径	r·₂	300.000	毫米
荷载		内压	p₁	60.000	kPa
荷载		外部压力	p₂	0.000	kPa

不可压缩材料 – 厚壁容器

该验算示例的目的是说明有限元单元中的体积锁定现象。在材料不可压缩情况下，当泊松比 ν 接近 0.5 时（橡胶材料、塑性材料），会出现此问题。在这种情况下，有限元位移趋于零。网格细化无法避免体积锁定。当使用不可压缩材料时，所有完全集成的单元将锁定。避免锁定的最简单方法是使用缩减积分。这种情况下积分点的数量会减少。该积分方案的精度比标准积分方案低一个数量级。 RFEM 中使用了缩减积分法，因此结果是正确的，如下所示。

解析解

其中的解析解与 VE0064 - 厚壁容器中的相同。末端开口容器的内外半径的径向挠度换算 u_r (r₁ ) ， u_r (r₂ ) 可以用下面的公式计算：

u_{r} (r_{1}) = \frac{r_{1}}{E} [σ_{t} (r_{1}) - ν σ_{r} (r_{1})],

u_{r} (r_{2}) = \frac{r_{2}}{E} [σ_{t} (r_{2}) - ν σ_{r} (r_{2})]

末端开口容器的内外半径的径向挠度

RFEM 设置

在 RFEM 5.06 和 RFEM 6.06 中建模
单元尺寸 l_FE = 2.000 mm
使用各向同性线弹性材料模型

结果

RFEM 6 Results – Total Deformation

数量	解析解	RFEM 6	比值	RFEM 5	比值
u_r (r₁ ) [mm]	29.988	29.986	1.000	29.987	1.000
u_r (r₂ ) [mm]	22.497	22.495	1.000	22.495	1.000

533x

验证示例000067 | 1

;