VE0067 | Nieściśliwy materiał - naczynie grubościenne

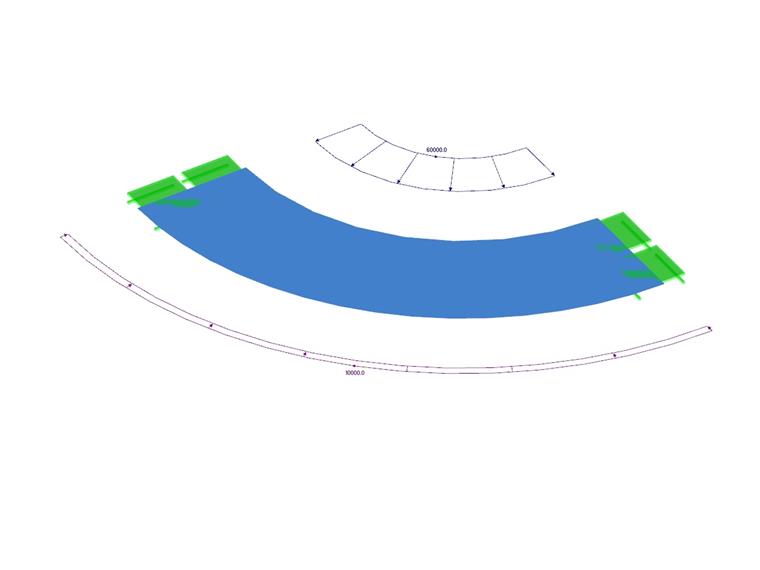
Opis prac

Ten przykład obliczeniowy jest modyfikacją VE0064 - Thick-walled Vessel, gdzie jedyną różnicą jest to, zbiornik jest nieściśliwy. Naczynie grubościenne jest obciążone ciśnieniem wewnętrznym i zewnętrznym. Zbiornik jest otwarty, dzięki czemu nie występuje naprężenie osiowe. Problem jest zamodelowany jako ćwiartka i opisany za pomocą poniższego zestawu parametrów. Pomijając ciężar własny, należy określić ugięcie promieniowe promienia wewnętrznego i zewnętrznego u_r (r₁ ), u_r (r₂ ).

Materiał	Sprężysto nieściśliwy	Moduł sprężystości	E	1,000	MPa
Materiał	Sprężysto nieściśliwy	współczynnik Poissona	ν	0.499	-
Geometria		Promień wewnętrzny	r₁	200.000	mm
Geometria		Promień zewnętrzny	r₂	300.000	mm
Obciążenie		Ciśnienie wewnętrzne	p₁	60.000	kPa
Obciążenie		Ciśnienie zewnętrzne	p₂	0.000	kPa

Materiał nieściśliwy – zbiornik grubościenny

Celem tego przykładu weryfikacyjnego jest pokazanie zjawiska blokowania objętościowego elementów skończonych. Problem ten może wystąpić w przypadku materiałów nieściśliwych, gdy współczynnik Poissona ν zbliża się do 0,5 (materiały gumowe, materiały w stanie plastycznym). W tym przypadku przemieszczenia elementów skończonych dążą do zera. Dzięki zagęszczeniu siatki nie można uniknąć blokowania objętości. W przypadku zastosowania materiału nieściśliwego wszystkie w pełni zintegrowane elementy zostają zablokowane. Najprostszym sposobem uniknięcia zablokowania jest zastosowanie zredukowanej integracji. W tym przypadku zmniejsza się liczba punktów całkowania. Schemat całkowania jest o jeden rząd mniej dokładny niż standardowy schemat całkowania. W programie RFEM stosowana jest metoda zredukowanego całkowania, dzięki czemu wynik jest prawidłowy, jak pokazano poniżej.

Rozwiązanie analityczne

Rozwiązanie analityczne jest takie samo, jak w przypadku VE0064 - Thick-walled Vessel. Żądane ugięcie promieniowe promienia wewnętrznego i zewnętrznego naczynia otwartego u_r (r₁ ), u_r (r₂ ) można wyznaczyć za pomocą następujących równań:

u_{r} (r_{1}) = \frac{r_{1}}{E} [σ_{t} (r_{1}) - ν σ_{r} (r_{1})],

u_{r} (r_{2}) = \frac{r_{2}}{E} [σ_{t} (r_{2}) - ν σ_{r} (r_{2})]

Ugięcie promieniowe wewnętrznego i zewnętrznego promienia zbiornika otwartego

Ustawienia RFEM

Modelowany w RFEM 5.06 i RFEM 6.06
Rozmiar elementu wynosi l_FE = 2.000 mm
Zastosowano izotropowy liniowo sprężysty model materiałowy

Wyniki

RFEM 6 Wyniki – Deformacja całkowita

Ilość	Rozwiązanie analityczne	RFEM 6	Stosunek	RFEM 5	Stosunek
u_r (r₁ ) [mm]	29.988	29.986	1,000	29.987	1,000
u_r (r₂ ) [mm]	22.497	22.495	1,000	22.495	1,000

535x

Przykład weryfikacji 000067 | 1

;