VE0067 | Inkompressibles Material - Dickwandiger Behälter

Beschreibung

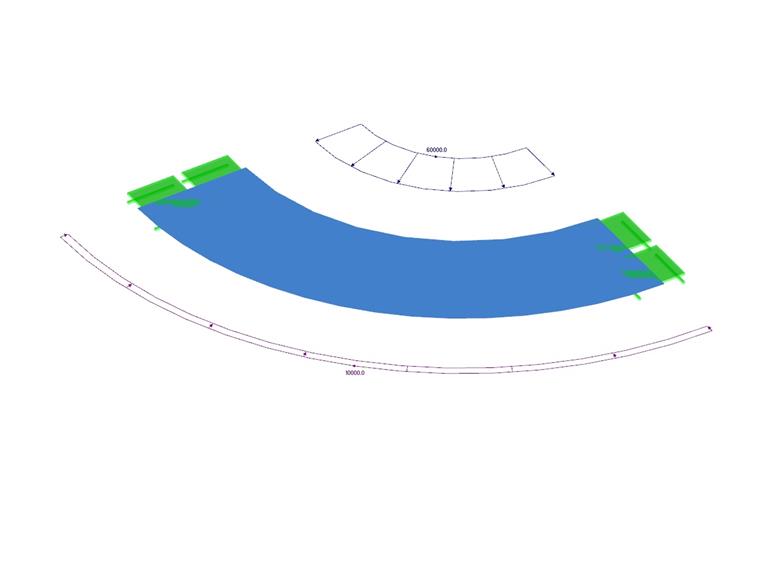
Dieses Verifikationsbeispiel ist eine Modifikation des VE0064 - Dickwandige Behälter, wo der einzige Unterschied ist dass das Material des Behälters inkompressibel ist. Ein dickwandiger Behälter wird durch inneren und äußeren Druck belastet. Das Ende des Behälters ist offen, folglich gibt es keine Normalspannung. Das Problem wird als Viertel-Modell modelliert und durch folgenden Parametersatz beschrieben. Ermitteln Sie die radiale Durchbiegung des Innen- und Außenradius u_r (r₁ ), u_r (r₂ ), ohne dabei das Eigengewicht zu berücksichtigen.

Material	Elastisch inkompressibel	Elastizitätsmodul	E	1,000	MPa
Material	Elastisch inkompressibel	Querdehnzahl	ν	0,499	-
Geometrie		Innenradius	r<sub>₁ </sub>	200,000	mm
Geometrie		Außenradius	_r2	300,000	mm
Last		Innendruck	p₁	60,000	kPa
Last		Außendruck	p₂	0,000	kPa

Inkompressibles Material - Dickwandiger Behälter

Ziel dieses Verifizierungsbeispiels ist es, das Phänomen der volumetrischen Verriegelung von finiten Elementen aufzuzeigen. Dieses Problem kann in inkompressiblen Materialfällen auftreten, wenn sich die Querdehnzahl ν dem Wert 0,5 nähert (Gummimaterialien, Materialien im plastischen Zustand). Die Finite-Element-Verschiebungen streben in diesem Fall gegen null. Die volumetrische Sperrung kann auch durch eine Netzverdichtung nicht vermieden werden. Alle voll integrierten Elemente sperren, wenn inkompressibles Material verwendet wird. Eine Sperrung kann am einfachsten mit einer reduzierten Integration umgangen werden. Die Anzahl der Integrationspunkte wird in diesem Fall reduziert. Das Integrationsschema ist eine Ordnung ungenauer als das Standard-Integrationsschema. In RFEM wird die reduzierte Integration verwendet, sodass das Ergebnis wie folgt korrekt ist.

Analytische Lösung

Die analytische Lösung ist die gleiche wie bei VE0064 - Dickwandiger Behälter. Gewünschte radiale Durchbiegung des Innen- und Außenradius des offenen Behälters u_r (r₁ ), u_r (r₂ ) kann mit folgenden Gleichungen bestimmt werden:

u_{r} (r_{1}) = \frac{r_{1}}{E} [σ_{t} (r_{1}) - ν σ_{r} (r_{1})],

u_{r} (r_{2}) = \frac{r_{2}}{E} [σ_{t} (r_{2}) - ν σ_{r} (r_{2})]

Radiale Durchbiegung des Innen- und Außenradius eines offenen Behälters

RFEM-Einstellungen

Modelliert in RFEM 5.06 und RFEM 6.06
Die Elementgröße beträgt l_FE = 2,000 mm
Es wird ein isotropes linear-elastisches Materialmodell vorausgesetzt.

Ergebnisse

RFEM 6-Ergebnisse – Totale Verformung

Anzahl	Analytische Lösung	RFEM 6	Verhältnis	RFEM 5	Verhältnis
u_r (r₁ ) [mm]	29,988	29,986	1,000	29,987	1,000
u_r (r₂ ) [mm]	22,497	22,495	1,000	22,495	1,000

535x

Verifikationsbeispiel 000067 | 1

;