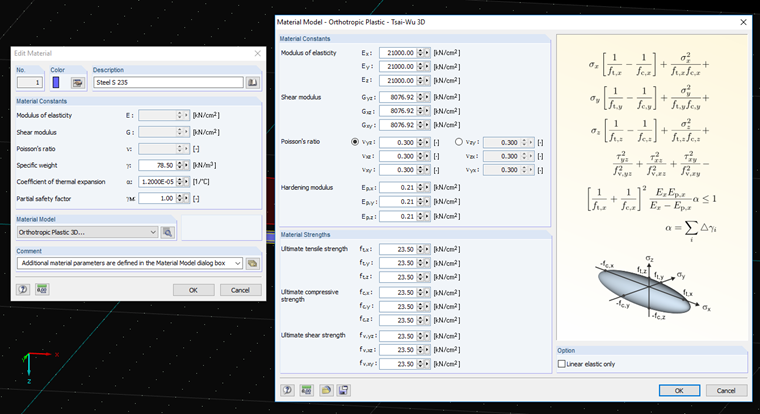
回复:
Tsai-Wu 材料模型结合了塑性和正交各向异性材料。 在建模时可以定义各向异性材料,如塑料或木材。 当材料进入塑性后,应力不再随应变增长, 保持恒定。 Der elastische Bereich entspricht dem Materialmodell "Orthotrop - 3D". 塑性区的屈服条件按照 Tsai-Wu:
这里:
Die Fließbedingung kann man sich als ellipsenförmige Fläche im sechsdimensionalen Spannungsraum vorstellen. 投影在各个平面上为一个椭圆。
Ist der Wert für fy(σ) kleiner als 1, so liegen die Spannungen im elastischen Bereich. Der plastische Bereich ist erreicht, sobald <nobr>fy(σ) = 1</nobr>. Werte größer als 1 sind unzulässig. Das Modell verhält sich ideal-plastisch, d. h. es findet keine Versteifung statt.