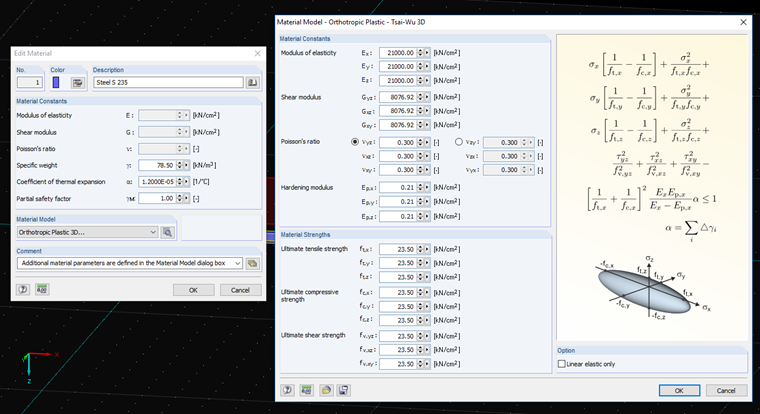
The Tsai-Wu material model combines plastic and orthotropic properties. In this way, it is possible to specifically model the materials with anisotropic properties, such as plastics or timber. If the material is plastified, the stresses remain constant. The redistribution is carried out according to the stiffnesses available in the individual directions. The elastic region corresponds to the "Orthotropic - 3D" material model. For the plastic area, the yielding according to Tsai-Wu applies:
with:
You can think of the stress criterion as an elliptical surface in a six-dimensional stress space. If one of the three stress components is applied as a constant value, the surface can be projected onto a three-dimensional stress space.
If the value for fy(σ) is smaller than 1, the stresses rest within the elastic area. The plastic area is reached as soon as fy(σ) = 1; values greater than 1 are not allowed. The model behavior is ideal-plastic, which means there is no stiffening.