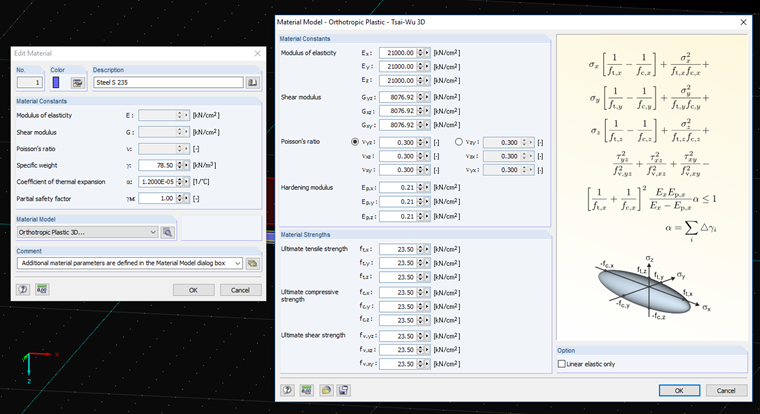
Das Materialmodell nach Tsai-Wu vereint plastische und orthotrope Eigenschaften. Damit sind spezielle Modellierungen von Werkstoffen mit anisotroper Charakteristik wie Kunststoff oder Holz möglich. Beim Plastizieren des Materials bleiben die Spannungen konstant. Es erfolgt eine Umlagerung in Abhängigkeit von den Steifigkeiten, die in die einzelnen Richtungen vorliegen. Der elastische Bereich entspricht dem Materialmodell "Orthotrop - 3D". Für den plastischen Bereich gilt folgende Fließbedingung nach Tsai-Wu:
mit:
Die Fließbedingung kann man sich als ellipsenförmige Fläche im sechsdimensionalen Spannungsraum vorstellen. Wird eine der drei Spannungskomponenten als konstanter Wert angesetzt, kann die Fläche auf einen dreidimensionalen Spannungsraum projiziert werden.
Ist der Wert für fy(σ) kleiner als 1, so liegen die Spannungen im elastischen Bereich. Der plastische Bereich ist erreicht, sobald fy(σ) = 1. Werte größer als 1 sind unzulässig. Das Modell verhält sich ideal-plastisch, d. h. es findet keine Versteifung statt.