在 RFEM 中按照欧洲规范 2 进行冲切设计

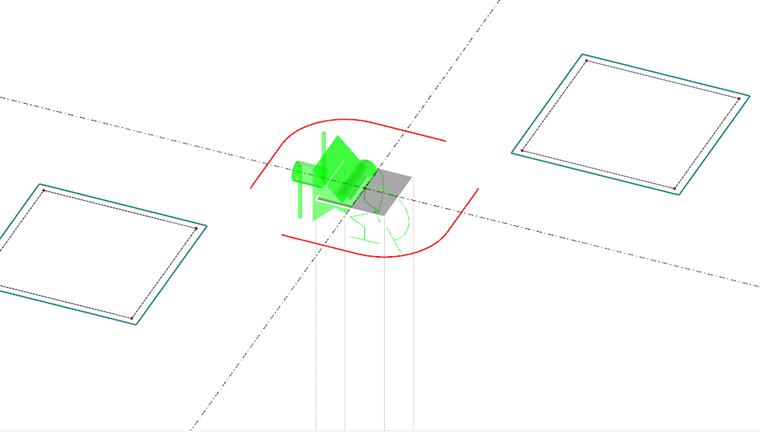
结构建模

RFEM 5 允许您对二维板和三维结构进行抗冲切试验。 附加模块 RF-PUNCH Pro 可以自动识别冲切位置，并推荐用于设计中。 可以单独设置用于查找冲切节点的集成过滤器。 这样，您可以很容易地对设计进行分类，例如平面、轮廓，以便非常容易地达到水平。

RF-PUNCH Pro 会自动识别 RFEM 模型中的冲切节点的类型（单柱、墙端或角部），以及冲切节点的面积（内柱、边缘柱或角部柱）。

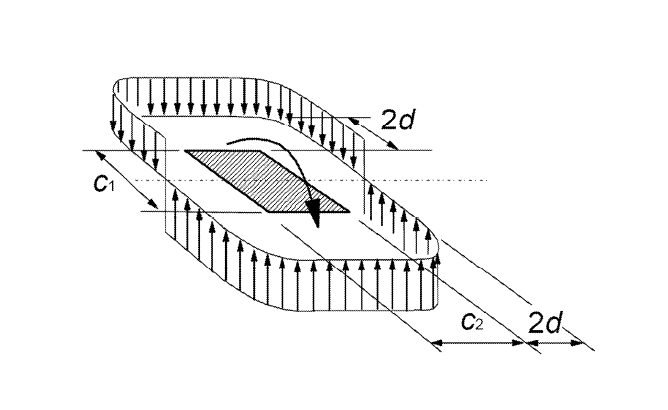
临界截面

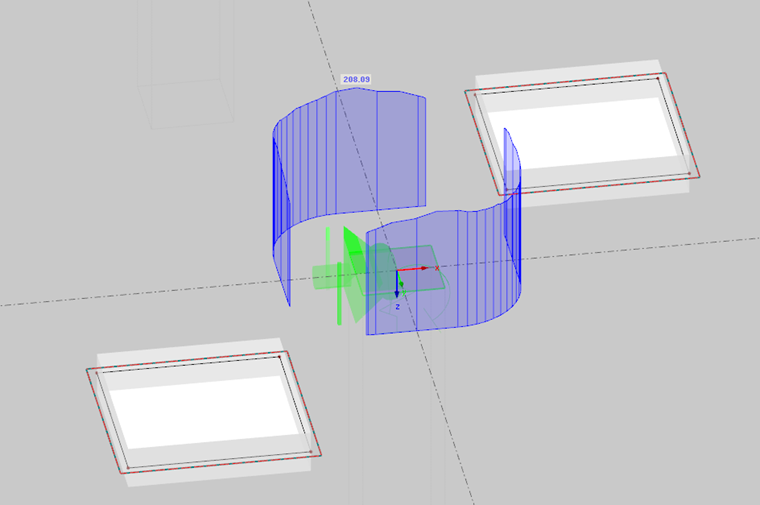
冲切剪切在基本控制区域内进行。 根据 Ch.在 EC 2 [1]的 6.4.2 中，板的控制周长位于距离荷载导入区域 2 d 处（d = 板的有效高度）。 在计算控制周长时需要考虑柱子的尺寸以及距离荷载导入区域 6 d 之前的板洞口。 RF-PUNCH Pro 会自动识别在有限元分析过程中建模的洞口。 此外，您还可以在模块中定义更小的洞口，例如在结构有限元计算中可以忽略。在确定基本控制周长时可以考虑这些因素。 附加模块的输入窗口中甚至在开始计算之前就已经显示了控制边界的几何形状。

Kritischer Rundschnitt um eine Stütze unter Berücksichtigung von zwei Öffnungen

对于楼板或基础，临界周长通常距离柱子边缘 2 d 。 根据 [1] 中 6.4.4 (2) 的规定，确定控制周长需要迭代计算。 德国国家规范附录[2] NCI 到 6.4.4(2) 允许简化计算楼板和细长基础，其中 λ = a_λ/d > 2 (其中 a_λ = 基础悬臂)。 在这种情况下，控制周长可以设置为距离 1d。 RF-PUNCH Pro 通常会通过迭代计算来找到基础或楼板的控制周长。

相关剪力 v_Ed

与控制周长相关的剪力设计值按照式（1）计算。 6.38，EC 2 [1]：

为了考虑不均匀的转动对称荷载，冲切荷载 V_Ed增加了荷载增量系数 β。 对于相邻跨度的长度差异不超过 25 % 的刚性固定结构，可以按照 EN 1992-1-1 中的图 6.21N [1]使用以下值 β：
β = 1,15 对于内柱
β = 1,4（对于边缘柱）
β = 1,5（对于角柱）
德语附录 [2] 中图 6.21N 对 β 系数进行了补充，即墙角 β = 1.35 和墙端 β = 1.2 ，并指定内柱的推荐值 β = 1.10。

关于确定荷载增量系数 β 的一般方法，请参见欧洲规范 2 [1]，第 1 章。 6.4.3(3)。 这里，系数 β 是假设 ¨ 在控制区域内完全塑性剪应力分布确定的。 按照 EN 1992-1-1 [1]，式式 (6.39) ，您获得：

全塑性的剪应力分布

EN 1992-1-1 [1] 的表达式（6.39）只规定了计算单轴荷载偏心时的 β，而德语附录 [2] 提供了考虑双轴荷载偏心的扩展表达式（NA.6.39.1）：

RF-PUNCH Pro 包含上述两种计算 β 的选项。 标准的方法是选择考虑完全塑性剪应力分布的模型。

RF-PUNCH Pro 直接从有限元计算中获取剪力 V_Ed的设计值来进行抗冲切试验。 在对柱子、节点支座和集中荷载进行冲切剪力设计时，可以根据柱子的轴力、支座力或集中力的荷载值来确定剪力。

此外，RF-PUNCH Pro 还允许您在有限元模型上创建控制周长，并确定作用在那里的剪力 V_Ed 。 为此，有以下两种选择：

• 控制区域内的剪力由同一个控制区域集成或平滑。 由此得出的设计剪力 V_Ed必须乘以荷载增量系数 β（见公式 6.38 [1]）。 如果使用全塑性剪切分布模型确定系数 β，则弯矩 M_Ed,x和 M_Ed,y也通过在板上设置的控制区域内积分板内力来确定。
• 在控制区域内选择最大的现有剪力进行抗冲切试验。 该方法考虑不均匀转动对称荷载的影响，采用最大值。 因此可以省略由系数 β 额外增加的剪力增量。

利用控制范围内的最大剪力值是确定冲切荷载设计值的最准确的方法，但也是最容易受到奇异性影响的方法。 特别是在有限元计算中直接从控制周长获取剪力时，应该注意冲切区域的有限元网格要足够细化。 通过有限元网格细化，建议在冲切节点和控制周长之间至少布置两个或三个单元。

截面处剪应力分布

对于基础和楼板，可以通过在迭代确定的控制周长内通过土压力来减小 V_Ed ；见 6.4.2(2)[1]。 如果按照德语附录 [2] 中的简化方法为细长基础创建基本控制周长 1 d，那么只能施加 50% 的土压力。 在 RF-PUNCH Pro 中可以选择两种设计形式。

设计形式

在进行抗冲切试验之前，程序会检查是否可以在没有抗冲切配筋的情况下进行设计。

不配置冲切钢筋的受冲切承载力

无剪切配筋的冲切承载力 v_Rd,c必须按照 EN 1992-1-1 [1] 的 6.4.4 (1) 计算，如下所示：
v_RD,c = C_RD,c ∙ k ∙ (100 ∙ ρ_l ∙ f_ck )^1/3 + k₁ ∙ σ_cp ≥ (v_min + k₁ ∙ σ_cp )
值:
C_Rd,c = 0.18/γ_c对于平板
C_Rd,c = 0.15/γ_c对于楼板/基础
k = 1 + √(200/d)
ρ_l,x/y = A_sl,x/y/(b_w · d_x/y )
ρ_l = √(ρ_l,x ∙ ρ_l,y ) ≤ 0.02
A_sl = 受拉钢筋面积
k₁ = 0.1
σ_cp = 控制区域内的正应力
v_min = 0.035 · k^3/2 · f_ck^1/2

在德语附录 [2]中，对上述参数进行了修改：
C_Rd,c = 0.18/γ_c对于平板
C_Rd,c = 0.18/γ_c ∙ (0.1 ∙ u₀/d + 0.6) 对于 u₀/d < 4 的平板内柱
C_Rd,c = 0.15/γ_c对于楼板/基础
ρ_l = √(ρ_l,x ∙ ρ_l,y ) ≤ min [0.02;0.5f_cd/f_yd ]
v_min = (0.00525/γ_c ) ∙ k^3/2 ∙ f_ck^1/2 for d ≤ 600 mm
v_min = (0.00375/γ_c ) · k^3/2 · f_ck^1/2 d > 800 mm

如果 v_Ed ≤ v_{Rd,c ，}则在没有额外抗冲切配筋的情况下满足抗冲切验算。 由于在结构上很难设计抗冲切配筋，所以通常可以避免使用抗冲切配筋，而采用最大允许的纵向配筋比 ρ_l 。 RF-PUNCH Pro 确定所需的纵向配筋率，以避免抗冲切配筋。 但是，也可以手动定义现有的纵向钢筋，以计算 V_Rd,c 。

最大冲切承载力 v_{Rd, max}

如果在没有抗冲切配筋的情况下无法进行冲切承载力设计，则在下一步中将计算最大受冲切承载力 v_Rd,max 。

根据 EN 1992-1-1 [1] 中 6.4.5 (3) 的规定，最大受冲切承载力在柱的外围进行。 计算的周边长度 u₀包含基本控制周长，并且可以直接在荷载导入面上确定。 柱子外围的最大冲切承载力 v_Rd,max按照 6.4.5 确定。 (3)，EN 1992-1-1 [1]，如下：
v_Rd,max = 0,4 · ν · f_cd
其中 ν = 0,6 · (1 - f_ck/250) (f_ck in [N/mm²])

作用在柱周围的剪力设计值来自：
v_Ed,u0 = β · V_Ed/(u₀ · d)

如果 v_Ed,u0 ≤ v_Rd,max ，则满足设计要求。

在德国国家规范附录 [2] 中，没有在柱的外围进行最大冲切承载力设计，而是在按照表达式 NA6.53.1 在基本控制周长 u1 中进行了计算：
v_Ed,u1 ≤ v_Rd,max = 1,4 · v_Rd,c,u1

抗冲切承载力（抗冲切配筋）

如果 v_Rd,max的计算成功，则在下一步中确定所需的抗冲切配筋。 所需的抗冲切配筋按照 EN 1992-1-1 [1] 中调整后的表达式 6.52 计算。 所需配筋 A_sw由以下公式得出：

冲切钢筋

根据 DIN EN 1992-1-1/NA [2]，在第一个受剪配筋计算截面上的配筋量必须增加系数 κ_sw,1 = 2.5，在第二个受剪截面上必须增加 κ_sw,2 = 1.4。配筋周长。

抗冲切配筋距离最外侧的计算截面最远距离为 1.5 d。 最外侧的计算截面所需的长度为 u_out,ef ，根据式 11 定义。 EC 2 [1] 的 6.54：

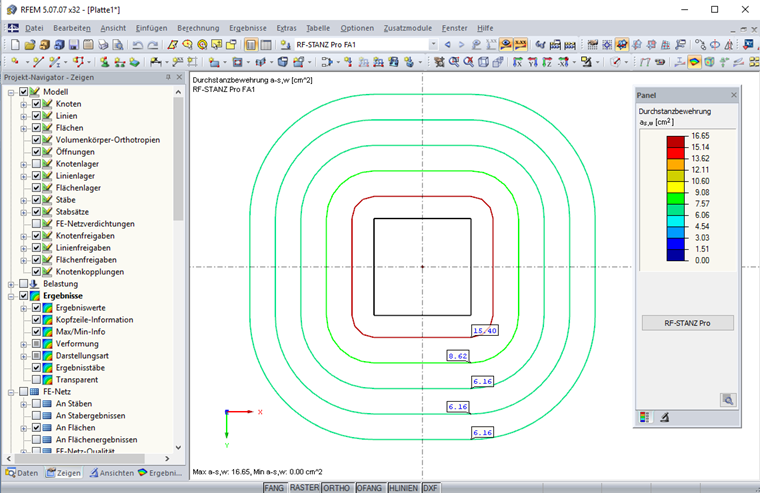
概述总结

如果没有软件解决方案，那么按照欧洲规范 2 对冲切验算的规定就无法有效地应用。 例如在控制区域内基于完全塑性剪力分布的模型计算荷载增量系数 β，或者对基础的基本控制周长进行迭代计算。 此外，建筑物的平面图设计方式更自由和更复杂，因此不可能遵循简化规则；因此也无法应用它们。 有限元结构分析软件 RFEM 的附加模块 RF-PUNCH Pro 允许您直接从有限元输入或有限元计算中获取基本控制周长和冲切验算设计荷载所需的所有数据。 因此可以非常简单有效地进行柱子、墙角和墙端的抗冲切试验。 对于柱子，可以选择考虑加宽柱帽的附加选项。 冲切试验的结果清楚地显示在结果表格中，包括与单个验算相关的所有中间结果。 在 RFEM 的图形窗口中可以图形方式显示计算结果以及所需的抗冲切配筋、剪力分布和冲切承载力。

参考