Dimensionnement des armatures de poinçonnement selon l’Eurocode 2 dans RFEM

Modélisation de la structure

RFEM 5 vous permet d'effectuer une vérification au poinçonnement pour les dalles 2D et les structures 3D. Le module additionnel RF-PUNCH Pro détecte automatiquement les positions de poinçonnement et les recommande pour la vérification. Un filtre intégré pour trouver les nœuds de poinçonnement peut être défini individuellement. De cette façon, vous pouvez facilement trier les dessins, par exemple par plan., un contour de la preuve, par exemple afin de niveaux très facilement possibles.

RF-PUNCH Pro reconnaît automatiquement le type de nœud de poinçonnement (poteaux simples, extrémités de voile ou coins), ainsi que la zone du nœud de poinçonnement (colonne intérieure, de bord ou d'angle) à partir du modèle RFEM.

Périmètre de contrôle

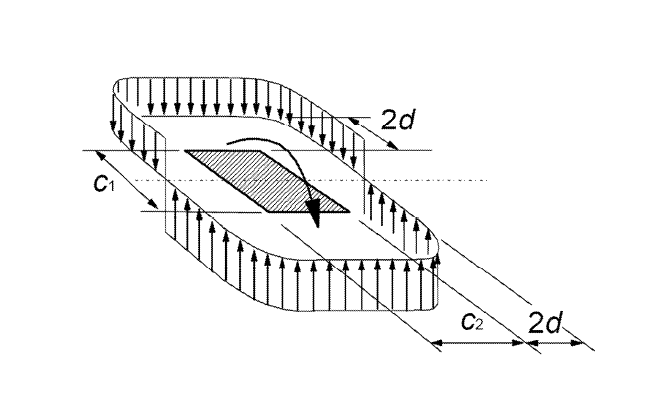
Le poinçonnement est effectué dans le périmètre de contrôle de base. D'après le ch. 6.4.2 de l'EC 2 [1] , le périmètre de contrôle pour les dalles est situé à une distance de 2 d (d = hauteur efficace de la dalle) de la surface de charge. La détermination de la géométrie du périmètre de contrôle nécessite la prise en compte des dimensions des poteaux ainsi que des ouvertures dans la dalle jusqu'à une distance de 6 d de la surface de charge. RF-PUNCH Pro reconnaît automatiquement les ouvertures modélisées lors de l'analyse aux éléments finis. De plus, vous pouvez également définir des ouvertures plus petites dans le module, qui sont négligeables dans le calcul de structure aux éléments finis, par exemple. Ceux-ci peuvent être considérés lors de la détermination du périmètre de contrôle de base. La géométrie du périmètre de contrôle est affichée dans la fenêtre de saisie du module additionnel avant même que vous ne commenciez le calcul.

Kritischer Rundschnitt um eine Stütze unter Berücksichtigung von zwei Öffnungen

Dans le cas de dalles de plancher ou de fondations, le périmètre critique est généralement à une distance de 2 d du bord du poteau. Selon 6.4.4 (2) [1], la détermination du périmètre de contrôle nécessite un calcul itératif. L'annexe nationale allemande [2] NCI à 6.4.4 (2) permet un calcul simplifié pour les dalles de plancher et les fondations minces avec_λ = a_λ/d > 2 (où a = porte-à-faux de la fondation). Dans ce cas, le périmètre de contrôle peut être défini à une distance de 1d. RF-PUNCH Pro effectue généralement un calcul itératif pour trouver le périmètre de contrôle des fondations ou des radiers.

Effort tranchant associé v_Ed

L'effort tranchant de calcul lié au périmètre de contrôle est calculé selon l'Éq. 6.38, EC 2 [1] :

Afin de considérer la charge symétrique de rotation inégale, la charge de poinçonnement V_Ed est augmentée du facteur d'incrément de charge . Pour les structures fixées de manière rigide dont les travées adjacentes ne diffèrent pas de plus de 25 % en longueur, vous pouvez utiliser les valeurs suivantes selon l'EN 1992-1-1, Figure 6.21N [1] :
β = 1,15 pour les poteaux internes
β = 1,4 pour les poteaux de bord
= 1,5 pour les poteaux d'angle
L'annexe allemande [2], Figure 6.21N, complète les facteurs β avec β = 1,35 pour les coins de voile et β = 1,2 pour les extrémités de voile, et spécifie la valeur recommandée pour les poteaux internes comme = 1,10.

Une méthode générale de détermination du facteur d'incrément de charge est décrite dans l'Eurocode 2 [1], Chap. 6.4.3 (3). Ici, le facteur β est déterminé en supposant la distribution de la contrainte de cisaillement entièrement plastique dans le périmètre de contrôle. Selon l'EN 1992-1-1 [1], l'Éq. (6.39), vous obtenez :

Distribution des contraintes de cisaillement entièrement plastique

Alors que l'expression (6.39) de l'EN 1992-1-1 [1] spécifie le calcul de pour l'excentrement de charge uniaxiale uniquement, l'annexe allemande [2] fournit l'expression développée (NA.6.39.1) pour considérer l'excentrement de charge biaxiale :

RF-PUNCH Pro inclut les deux options de calcul de mentionnées ci-dessus. La méthode standard consiste à sélectionner le modèle en considérant la distribution de la contrainte de cisaillement entièrement plastique.

RF-PUNCH Pro prend la valeur de calcul de l'effort tranchant V_Ed directement à partir du calcul aux éléments finis pour effectuer la vérification du poinçonnement. Dans le cas de la vérification du poinçonnement pour les poteaux, les appuis nodaux et les charges concentrées, vous pouvez déterminer l'effort tranchant à partir de l'effort normal du poteau, de l'effort d'appui ou de la valeur de charge de la force concentrée active.

De plus, RF-PUNCH Pro permet de créer le périmètre de contrôle sur un modèle aux éléments finis et d'y déterminer l'effort tranchant actif V_Ed. Pour ce faire, deux possibilités s'offrent à vous :

• Les efforts tranchants existants dans le périmètre de contrôle sont intégrés ou lissés par le même périmètre de contrôle. L'effort tranchant de calcul résultant V_Ed doit ensuite être multiplié par le facteur d'incrément de charge (voir l'Éq. 6.38 [1]). Si le facteur β est déterminé à l'aide du modèle de distribution de cisaillement entièrement plastique, les moments fléchissants M_Ed,x et M_Ed,y sont également déterminés en intégrant les efforts internes à la dalle dans le périmètre de contrôle défini sur la dalle.
• La valeur maximale de l'effort tranchant existant dans le périmètre de contrôle est utilisée pour la vérification du poinçonnement. Cette méthode prend en compte l'effet de la charge symétrique de rotation inégale en utilisant la valeur maximale. Par conséquent, un incrément supplémentaire de l'effort tranchant du facteur β peut être omis.

Bien que l'utilisation de la valeur maximale de l'effort tranchant dans le périmètre de contrôle soit la méthode la plus précise pour déterminer la valeur de calcul de la charge de poinçonnement, c'est également la méthode la plus sensible aux effets de singularité. En particulier, veillez à ce que le maillage EF soit suffisamment affiné dans les zones de poinçonnement lorsque vous prenez les efforts tranchants directement à partir du périmètre de contrôle dans le calcul aux éléments finis. Il est recommandé de disposer au moins deux ou trois éléments entre les nœuds de poinçonnement et le périmètre de contrôle à l'aide du raffinement de maillage EF.

Distribution des contraintes de cisaillement dans la section

Dans le cas de fondations et de dalles, vous pouvez réduire V_Ed par la pression au sol dans le périmètre de contrôle déterminé de manière itérative ; voir 6.4.2 (2) [1]. Si vous créez le périmètre de contrôle de base de 1 d pour les fondations minces selon la méthode simplifiée de l'annexe allemande [2], vous ne pouvez appliquer que 50 % de la pression du sol. Les deux formes de vérification peuvent être sélectionnées dans RF-PUNCH Pro.

Formulaire de calcul

Avant la vérification du poinçonnement, le programme vérifie si la vérification peut être effectuée sans poinçonnement d'armatures.

Résistance au poinçonnement de dalles sans armatures de poinçonnement

La résistance au poinçonnement sans armatures d'effort tranchant v_Rd,c doit être déterminée comme suit selon 6.4.4 (1), EN 1992-1-1 [1] :
v_RD,c = C_RD,c k ∙ (100 ∙ ρ_l ∙ f_ck )^1/3 + k₁ σ_cp ≥ (v_min + k₁ ∙ σ_cp )
où
C_Rd,c = 0,18/γ_c pour les dalles plates
C_Rd,c = 0,15/γ_c pour les radiers/fondations
k = 1 + (200/d)
_l,x/y = A_sl,x/y/(b_w · d_x/y )
_l = (ρ_l,x ∙_l,y ) 0,02
A_sl = aire des armatures de traction
k₁ = 0,1
_cp = contrainte normale dans le périmètre de contrôle
v_min = 0,035 · k^3/2 · f_ck^1/2

Dans l'annexe allemande [2], les paramètres mentionnés ci-dessus sont modifiés comme suit :
C_Rd,c = 0,18/γ_c pour les dalles plates
C_Rd,c = 0,18/γ_c ∙ (0,1 u₀/d + 0,6) dans le cas de poteaux internes de dalles plates avec u₀/d < 4
C_Rd,c = 0,15/γ_c pour les radiers/fondations
_l = √(ρ_l,x ∙_l,y ) ≤ min [0,02;0,5f_cd/f_yd ]
v_min = (0,00525/γ_c ) k^3/2 f_ck^1/2 pour d 600 mm
v_min = (0,00375/γ_c ) · k^3/2 · f_ck^1/2 pour d > 800 mm

La vérification du poinçonnement est effectuée sans armatures de poinçonnement supplémentaires si v_Ed v_Rd,c. En raison de la difficulté de calcul des armatures d'effort tranchant, il est généralement possible d'éviter d'utiliser des armatures de poinçonnement et d'appliquer à la place le rapport d'armatures longitudinales maximal admissible_l. RF-PUNCH Pro détermine le rapport d'armatures longitudinales requis afin d'éviter les armatures de poinçonnement. Cependant, il est également possible de définir manuellement les armatures longitudinales existantes pour le calcul de V_Rd,c.

Résistance maximale au poinçonnement v_{Rd, max}

Si la vérification du poinçonnement est impossible sans poinçonnement des armatures, la résistance maximale au poinçonnement v_Rd,max est calculée à l'étape suivante.

Selon 6.4.5 (3) EN 1992-1-1 [1], la résistance maximale au poinçonnement est déterminée à la périphérie d'un poteau. La longueur de périphérie considérée u₀ englobe le périmètre de contrôle de base et peut être déterminée directement sur la surface de charge. La résistance maximale au poinçonnement à la périphérie du poteau v_Rd,max est déterminée selon 6.4.5. (3), EN 1992-1-1 [1], comme suit :
v_Rd,max = 0,4 · ν · f_cd
où = 0,6 · (1 - f_ck/250) (f_ck en [N/mm²])

L'effort tranchant de calcul agissant sur la périphérie du poteau résulte de :
v_Ed,u0 = · V_Ed/(u₀ · d)

Le calcul est effectué si v_Ed,u0 v_Rd,max.

Dans l'annexe nationale allemande [2], le calcul de la résistance maximale au poinçonnement n'est pas effectué à la périphérie du poteau, mais dans le périmètre de contrôle de base u1 selon l'expression NA6.53.1 comme suit :
v_Ed,u1 v_Rd,max = 1,4 · v_Rd,c,u1

Résistance au poinçonnement avec armatures de poinçonnement

Si la vérification de v_Rd,max a été effectuée avec succès, l'armature de poinçonnement requise est déterminée à l'étape suivante. L'armature de poinçonnement requise est calculée selon l'expression ajustée 6.52 de l'EN 1992-1-1 [1]. L'armature requise A_sw résulte de l'équation suivante :

4-Armatures-de-poinconnement

Selon DIN EN 1992-1-1/NA [2], la quantité d'armatures dans le premier périmètre d'armatures d'effort tranchant doit être augmentée du facteur κ_sw,1 = 2,5 et de κ_sw,2 = 1,4 dans le deuxième périmètre d'effort tranchant périmètre d'armatures.

Les armatures d'effort tranchant doivent être placées à une distance maximale de 1,5 d du périmètre le plus à l'extérieur. La longueur requise du périmètre le plus à l'extérieur est u_out,ef, qui est définie selon l'Éq. 6.54 de l'EC 2 [1] :

Conclusion

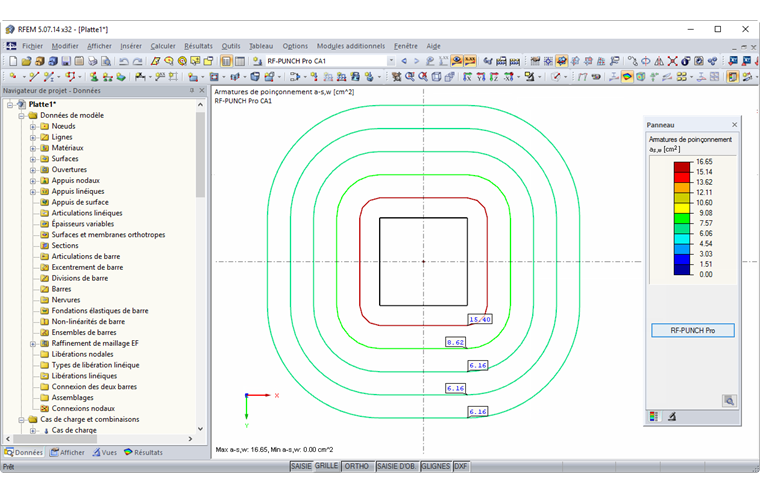
Les dispositions pour le calcul du poinçonnement selon l'Eurocode 2 ne peuvent pas être appliquées efficacement sans une solution logicielle. Citons par exemple le calcul du facteur d'incrément de charge basé sur le modèle avec une distribution des forces de cisaillement entièrement plastique dans le périmètre de contrôle ou le calcul itératif du périmètre de contrôle de base des fondations. De plus, les plans des bâtiments sont calculés de manière plus libre et plus complexe, il est donc impossible de suivre les règles de simplification ; elles ne peuvent donc pas non plus être appliquées. Toutes les données nécessaires à la détermination géométrique du périmètre de contrôle de base et des charges de calcul pour la vérification du poinçonnement peuvent être extraites du module additionnel RF-PUNCH Pro du logiciel de calcul aux éléments finis RFEM. Ainsi, la vérification au poinçonnement des poteaux, des coins de mur et des extrémités de mur peut être effectuée très facilement et efficacement. Pour les poteaux, il est possible de considérer un en-tête de poteau agrandi. Les résultats de la vérification par poinçonnement sont affichés dans des tableaux de résultats clairs, y compris tous les résultats intermédiaires pertinents pour les différentes vérifications. Les résultats ainsi que les armatures de poinçonnement requises, la répartition de l'effort tranchant et les résistances au poinçonnement peuvent être affichés graphiquement dans la fenêtre graphique de RFEM.

Références