Расчет на продавливание по норме Еврокод 2 в RFEM

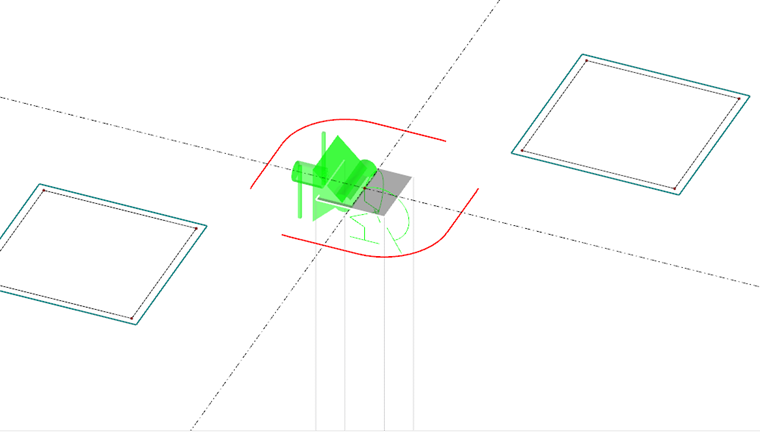
Моделирование конструкции

RFEM 5 позволяет выполнять расчет на продавливание как двухмерных плит, так и трехмерных конструкций. Дополнительный модуль RF-PUNCH Pro автоматически определяет места продавливания и рекомендует их для расчета. Встроенный фильтр для поиска узлов продавливания можно настроить индивидуально. Таким образом, вы можете легко отсортировать рисунки, например, по плоскостям, наброскам улик, например, для очень удобного выравнивания.

RF-PUNCH Pro автоматически распознает тип узла высечки (отдельные колонны, торцы стен или углы), а также площадь узла высечки (внутренние, краевые или угловые колонны) из модели RFEM.

Критический контур

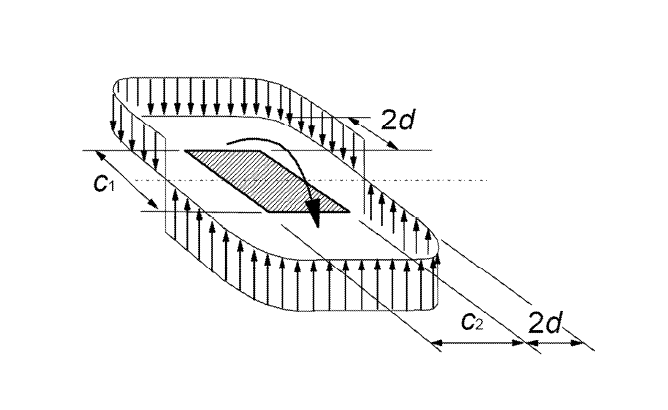
Пробивной сдвиг выполняется по периметру основного контроля. По мнению гл. 6.4.2 EC 2 [1] , контрольный периметр для плит располагается на расстоянии 2 d (d = эффективная глубина плиты) от поверхности нагрузки. Определение геометрии периметра контроля требует учета размеров колонн, а также отверстий в плитах на расстоянии до 6 d от поверхности нагрузки. RF-PUNCH Pro автоматически распознает отверстия, смоделированные во время анализа методом конечных элементов. Кроме того, вы также можете определить в модуле отверстия меньшего размера, которыми можно пренебречь, например, при расчете конструктивных элементов. Их можно учесть при определении основного периметра контроля. Геометрия контрольного периметра отображается в окнах ввода дополнительного модуля еще до того, как вы начнете расчет.

Kritischer Rundschnitt um eine Stütze unter Berücksichtigung von zwei Öffnungen

В случае плит перекрытия или фундамента критический периметр обычно находится на расстоянии 2d от края колонны. Согласно 6.4.4 (2) [1], для определения периметра управления требуется итерационный расчет. Немецкое национальное приложение [2] NCI к 6.4.4 (2) допускает упрощенный расчет для плит перекрытия и тонких фундаментов с λ = a_λ/d> 2 (где_λ = консоль фундамента). В этом случае периметр контроля может быть установлен на расстоянии 1d. Как правило, RF-PUNCH Pro выполняет итерационные вычисления для определения контрольного периметра фундаментов или плит перекрытия.

Связанная поперечная сила v_Ed

Расчетная поперечная сила, относящаяся к периметру контроля, рассчитывается по формуле. 6.38, EC 2 [1]:

Чтобы учесть неравномерную вращательно-симметричную нагрузку, пробивающую нагрузку V_Ed увеличивают на коэффициент приращения нагрузки β. Для жестко закрепленных конструкций, у которых длина соседних пролетов не отличается по длине более чем на 25%, можно использовать следующие значения β в соответствии с EN 1992-1-1, рисунок 6.21N [1]:
β = 1,15 для внутренних колонн
β = 1,4 для краевых колонн
β = 1,5 для угловых колонн
Немецкое приложение [2], рисунок 6.21N, дополняет коэффициенты β с β = 1,35 для углов стен и β = 1,2 для концов стен и определяет рекомендуемое значение для внутренних колонн как β = 1,10.

Общий метод определения коэффициента увеличения нагрузки β описан в Еврокоде 2 [1], гл. 6.4.3 (3). Здесь коэффициент β определяется в предположении, что полностью пластическое распределение напряжения сдвига в контрольном периметре. В соответствии с EN 1992-1-1 [1], уравнение. (6.39), получаем:

Полностью пластическое распределение касательного напряжения

В то время как выражение (6.39) стандарта EN 1992-1-1 [1] определяет расчет β только для эксцентриситета одноосной нагрузки, приложение Германии [2] предоставляет расширенное выражение (NA.6.39.1) для учета эксцентриситета двухосной нагрузки:

RF-PUNCH Pro включает оба варианта расчета β, упомянутые выше. Стандартный метод заключается в выборе модели с учетом полностью пластического распределения напряжения сдвига.

RF-PUNCH Pro берет расчетное значение поперечной силы V_Ed непосредственно из расчета МКЭ для расчета на продавливание. В случае расчета на продавливание колонн, узловых опор и сосредоточенных нагрузок вы можете определить поперечную силу на основе осевой силы колонны, опорной силы или значения нагрузки действующей сосредоточенной силы.

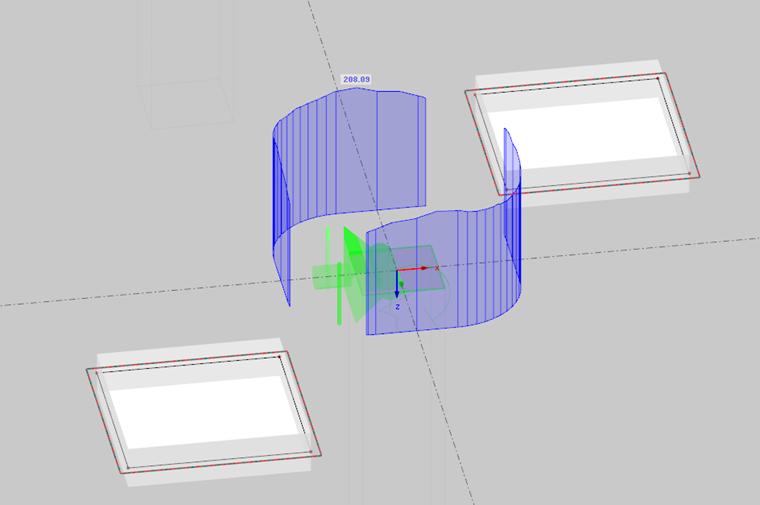
Кроме того, RF-PUNCH Pro позволяет создать контрольный периметр на модели FEM и определить действующую поперечную силу V_Ed. Для этого есть два варианта:

• Существующие поперечные силы в контрольном периметре интегрируются или сглаживаются тем же контрольным периметром. Результирующая расчетная поперечная сила V_Ed затем должна быть умножена на коэффициент приращения нагрузки β (см. Уравнение 6.38 [1]). Если коэффициент β определяется с использованием модели распределения полностью пластического сдвига, оба изгибающих момента M_{Ed, x} и M_{Ed, y} также определяются путем интегрирования внутренних сил плиты в контрольном периметре плиты.
• Максимальное значение существующей поперечной силы в контрольном периметре используется для расчета продавливания. Этот метод учитывает влияние неравномерной вращательно-симметричной нагрузки с помощью максимального значения. Следовательно, дополнительное приращение поперечной силы на коэффициент β может быть пропущено.

Хотя использование максимального значения поперечной силы в контрольном периметре является наиболее точным методом определения расчетного значения пробивающей нагрузки, он также является наиболее чувствительным к эффектам сингулярности. В частности, при расчете сил сдвига непосредственно с контрольного периметра при расчете МКЭ следует обратить внимание на достаточную детализацию сетки КЭ в областях продавливания. Между узлами штамповки и контрольным периметром рекомендуется расположить не менее двух или трех элементов с помощью измельчения сетки КЭ.

Распределение касательных напряжений в сечении

В случае фундаментов и плит перекрытия V_Ed можно уменьшить за счет давления грунта в пределах итеративно определенного контрольного периметра; см. 6.4.2 (2) [1]. Если вы создадите основной контрольный периметр на 1 d для тонких фундаментов в соответствии с упрощенным методом, указанным в приложении [2], вы сможете применить только 50% давления грунта. Обе формы дизайна могут быть выбраны в RF-PUNCH Pro.

Форма дизайна

Перед расчетом на продавливание среза программа проверяет, можно ли выполнить расчет без продавливания арматуры.

Сопротивление сдвигу при продавливании, без арматуры на продавливание

Сопротивление продавливанию без арматуры v_{Rd, c} должно быть определено в соответствии с 6.4.4 (1), EN 1992-1-1 [1] следующим образом:
v_{RD, c} = C_{RD, c} ∙ k ∙ (100 ∙ ρ_l ∙ f_ck )^1/3 + k₁ ∙ σ_cp ≥ (v_min + k₁ ∙ σ_cp )
где
C_{Rd, c} = 0,18/γ_c для плоских плит
C_{Rd, c} = 0,15/γ_c для плит перекрытия/фундамента
k = 1 + √ (200/д)
ρ_{l, x/y} = A_{sl, x/y}/(b_w · d_x/y )
ρ_l = √ (ρ_{l, x} ∙ ρ_{l, y} ) ≤ 0,02
A_sl = площадь растянутой арматуры
k₁ = 0,1
σ_cp = нормальное напряжение в контрольном периметре
v_min = 0,035 · k^3/2 · f_ck^1/2

В немецком приложении [2] упомянутые выше параметры изменены следующим образом:
C_{Rd, c} = 0,18/γ_c для плоских плит
C_{Rd, c} = 0,18/γ_c ∙ (0,1 ∙ u₀/d + 0,6) в случае внутренних колонн из плоских плит с u₀/d <4
C_{Rd, c} = 0,15/γ_c для плит перекрытия/фундамента
ρ_l = √ (ρ_{l, x} ∙ ρ_{l, y} ) ≤ min [0,02; 0,5f_кд/_ярд ]
v_min = (0,00525/γ_c ) ∙ k^3/2 ∙ f_ck^1/2 для d ≤ 600 мм
v_min = (0,00375/γ_c ) · k^3/2 · f_ck^1/2 для d> 800 мм

Расчет на продавливание выполняется без дополнительной продавливания арматуры, если v_Ed ≤ v_{Rd, c}. Из-за конструктивно сложной конструкции поперечной арматуры обычно можно попытаться избежать использования продольной арматуры и вместо этого применить для этой цели максимально допустимый коэффициент продольной арматуры ρ_l. RF-PUNCH Pro определяет необходимый коэффициент продольной арматуры, чтобы избежать армирования при продавливании. Однако также можно определить существующую продольную арматуру для расчета V_{Rd, c} вручную.

Максимальное сопротивление продавливанию v_{Rd, max}

Если расчет на продавливание невозможно без арматуры продавливания, на следующем этапе рассчитывается максимальное сопротивление продавливанию v_{Rd, max}.

Согласно 6.4.5 (3) EN 1992-1-1 [1], максимальное сопротивление продавливанию достигается на периферии колонны. Рассматриваемая длина периферии u₀ охватывает основной периметр управления и может быть определена непосредственно на поверхности нагрузки. Максимальное сопротивление продавливанию на периферии колонны v_{Rd, max} определяется в соответствии с 6.4.5. (3), EN 1992-1-1 [1], следующим образом:
v_{Rd, max} = 0,4 · ν · f_cd
где ν = 0,6 · (1 - f_ck/250) (f_ck в [Н/мм²])

Действующая расчетная поперечная сила на периферии колонны возникает в результате:
v_{Ed, u0} = β · V_Ed/(u₀ · d)

Расчет выполняется, если v_{Ed, u0} ≤ v_{Rd, max}.

В Немецком национальном приложении [2] расчет максимального сопротивления продавливанию выполняется не на периферии колонны, а в основном контрольном периметре u1 в соответствии с выражением NA6.53.1 следующим образом:
v_{Ed, u1} ≤ v_{Rd, max} = 1,4 · v_{Rd, c, u1}

Сопротивление продавливанию с армированием на продавливание

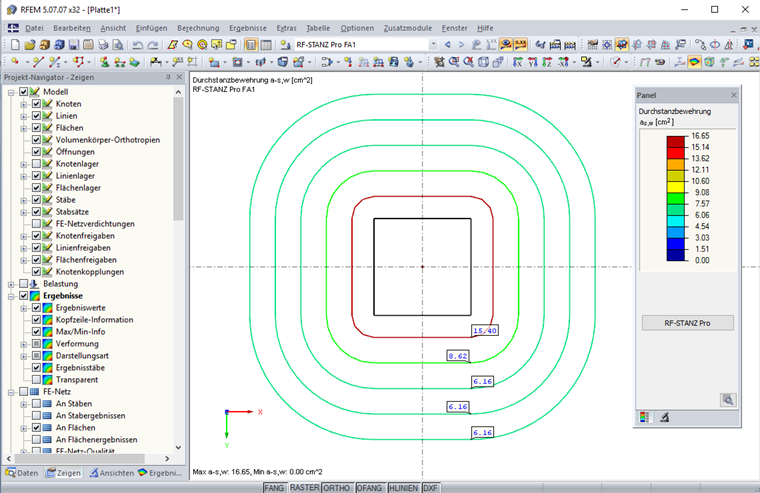
Если расчет v_{Rd, max} был выполнен успешно, на следующем этапе определяется необходимая арматура для продавливания. Требуемая арматура при продавливании рассчитывается согласно скорректированному выражению 6.52 стандарта EN 1992-1-1 [1]. Требуемая арматура A_sw определяется следующим уравнением:

Арматуры от продавливания

Согласно DIN EN 1992-1-1/NA [2], количество арматуры в первом периметре поперечной арматуры должно быть увеличено на коэффициент κ_{sw, 1} = 2,5, и на κ_{sw, 2} = 1,4 во втором сдвиге. периметр армирования.

Арматуру от продавливания следует размещать на расстоянии 1,5 d от внешнего периметра. Требуемая длина внешнего периметра u_{out, ef}, которая определяется согласно формуле. 6.54 EC 2 [1]:

Заключение

Положения по расчету на продавливание по Еврокоду 2 не могут быть эффективно применены без программного решения. Примером может служить расчет коэффициента приращения нагрузки β на основе модели с полностью пластическим распределением поперечной силы в контрольном периметре или итерационный расчет основной контрольной площади периметра фундаментов. Кроме того, планы этажей построек более свободны и сложны, поэтому соблюдение правил упрощения невозможно; таким образом, они также не могут быть применены. Дополнительный модуль RF-PUNCH Pro к программе расчета конструктивных элементов конструкций RFEM позволяет вам получить все данные, необходимые для геометрического определения основного контрольного периметра и расчетных нагрузок для расчета на продавливание, непосредственно из записей МКЭ или расчета МКЭ. Таким образом, расчет на продавливание колонн, углов стен и концов стен может быть выполнен очень легко и эффективно. Для столбцов есть дополнительная возможность рассмотреть увеличенный заголовок столбца. Результаты расчета на продавливание отображаются в наглядных таблицах результатов, включая все промежуточные результаты, относящиеся к отдельным расчетам. Результаты, а также требуемая арматура при продавливании, распределение поперечных сил и сопротивления продавливанию могут быть отображены графически в графическом окне RFEM.

Ссылки