Posouzení na protlačení podle Eurokódu 2 v programu RFEM

Modelování konstrukce

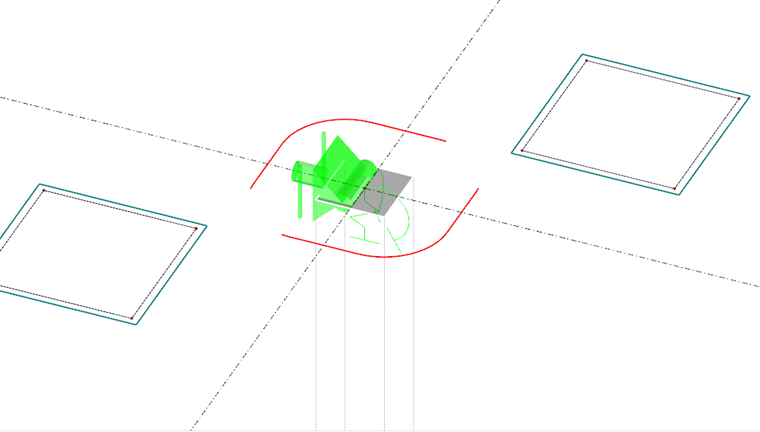
V programu RFEM 5 lze na protlačení posuzovat 2D desky i 3D konstrukce. Přídavný modul RF-PUNCH Pro automaticky rozpozná místa, kterým hrozí protlačení, a navrhne u nich provést výpočet. Filtr, který je do programu integrován a kterým se hledají uzly protlačení, lze individuálně nastavit. Lze tak velmi snadno rozčlenit posouzení například podle rovin.

RF-PUNCH Pro automaticky rozpozná na základě vstupních údajů, které o konstrukci zadáme v programu RFEM, typ uzlu protlačení (jednotlivý sloup, roh nebo konec stěny) a také polohu bodu protlačení (vnitřní, okrajový nebo rohový sloup).

Kontrolovaný obvod

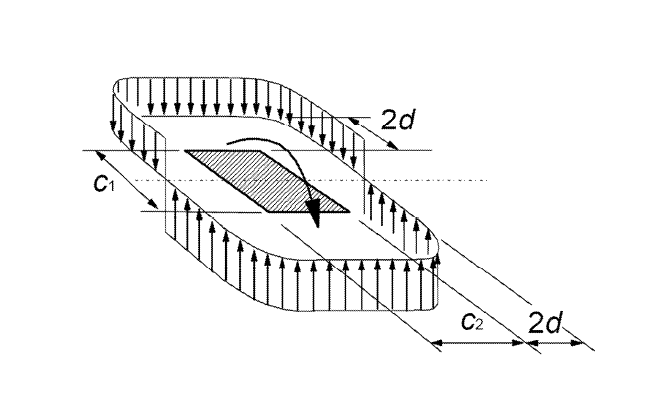
Posouzení na protlačení se provádí v takzvaném základním kontrolovaném obvodu. Podle Eurokódu 2 [1], čl. 6.4.2 lze základní kontrolovaný obvod u desek obvykle uvažovat ve vzdálenosti 2 d (d = účinná výška desky) od zatěžované plochy. Geometrie základního kontrolovaného obvodu se stanoví na základě rozměrů sloupu a také otvorů v desce do vzdálenosti 6 d od zatěžované plochy. RF-PUNCH Pro automaticky rozpozná otvory vytvořené v modelu během posouzení metodou konečných prvků (MKP). Dále lze také v přídavném modulu RF-PUNCH Pro zadat menší otvory (které lze například při statickém výpočtu desky MKP zanedbat), které se pak zohlední při stanovení geometrie základního kontrolovaného obvodu. Geometrie kontrolovaného obvodu se zobrazí ve vstupních dialozích tohoto modulu již před spuštěním výpočtu.

Při posouzení desek nebo základů se základní kontrolovaný obvod zpravidla uvažuje ve vzdálenosti do 2 d od okraje sloupu. Podle 6.4.4 (2) [1] se má základní kontrolovaný obvod stanovit iteračním výpočtem. Německá národní příloha [2] připouští v NCI ke 6.4.4 (2) u desek a štíhlých základů, pro které platí λ = aλ / d> 2 (kde a_λ = přesah základu), zjednodušený výpočet. Základní kontrolovaný obvod lze přitom uvažovat ve vzdálenosti 1 d. V přídavném modulu RF-PUNCH Pro se obecně u desek a základů používá ke stanovení základního kontrolovaného obvodu iterační výpočet.

Posouvající síla v_Ed

Návrhová posouvající síla vztažená k základnímu kontrolovanému obvodu se vypočítá pomocí rovnice 6.38 z Eurokódu 2 [1]:

kde
u₁ = délka uvažovaného kontrolovaného obvodu
d = průměrná účinná výška desky
β = součinitel zvyšující zatížení, kterým se zohledňuje nerovnoměrné rozdělení posouvající síly v základním kontrolovaném obvodu
V_Ed = návrhové zatížení pro protlačení

Abychom zohlednili nerovnoměrné zatížení, zvýší se zatížení pro protlačení V_Ed součinitelem β. V případě neposuvných systémů, u nichž se rozpětí sousedních polí neliší více než o 25 %, lze podle EN 1992-1-1, obr. 6.21N [1] použít následující hodnoty součinitelů β:
β = 1,15 pro vnitřní sloupy
β = 1,4 pro okrajové sloupy
β = 1,5 pro rohové sloupy
Německá příloha [2] doplnila obrázek 6.21N o hodnotu součinitele β = 1,35 pro rohy stěn a β = 1,20 pro konce stěn a také upravila doporučenou hodnotu pro vnitřní sloupy na β = 1,10.

Obecně platnou metodu, kterou se stanoví součinitel zvyšující zatížení β, popisuje Eurokód 2 [1] v článku 6.4.3 (3). Při výpočtu součinitele β se přitom uvažuje plně plastické rozdělení smykového napětí v základním kontrolovaném obvodu. Podle EN 1992-1-1 [1] rovnice (6.39) dostaneme:

kde
k = součinitel závisející na poměru mezi rozměry sloupu, viz tabulka 6.1 [1]
M_Ed = moment okolo těžiště základního kontrolovaného obvodu
W₁ = modul, který odpovídá rozdělení smyku a je funkcí základního kontrolovaného obvodu

Zatímco EN 1992-1-1 [1] předkládá pro výpočet β rovnici (6.39), která platí pouze v případě jednoosé výstřednosti zatížení, obsahuje německá příloha [2] následovně rozšířenou rovnici (NA.6.39.1) zohledňující dvouosou výstřednost zatížení:

V přídavném modulu RF-PUNCH Pro máme k dispozici obě výše uvedené možnosti výpočtu β. Za standardní metodu se přitom považuje model s plně plastickým rozdělením smykového napětí.

RF-PUNCH Pro přebírá návrhovou hodnotu posouvající síly V_Ed pro posouzení na protlačení přímo z výpočtu MKP. Pro posouzení na protlačení na sloupech, uzlových podporách a v místě působení osamělých břemen lze návrhovou posouvající sílu určit z normálové síly ve sloupu, z podporové síly nebo z hodnoty zatížení vlivem působící osamělé síly.

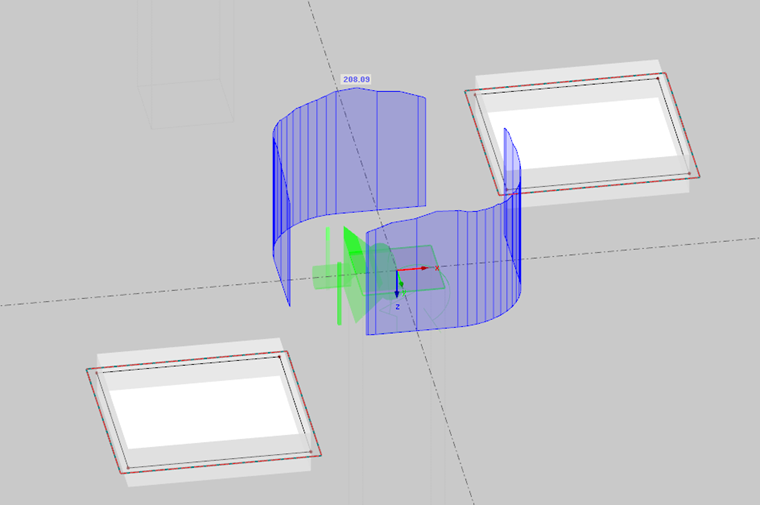
Další možností je nechat stanovit přídavným modulem RF-PUNCH Pro v modelu pro výpočet MKP základní kontrolovaný obvod a vypočítat v něm působící posouvající sílu V_Ed. Nabízí se nám přitom následující dvě volby:

• Posouvající síly působící v základním kontrolovaném obvodu budou integrovány, respektive vyhlazeny po celém kontrolovaném obvodu. Získáme tak návrhovou posouvající sílu V_Ed, kterou je následně třeba vynásobit součinitelem zvyšujícím zatížení β (srov. rovnici 6.38 [1]). Pokud jsme součinitel β stanovili na modelu s plně plastickým rozdělením smykového napětí, pak se oba ohybové momenty M_Ed,x a M_Ed,y určí rovněž z integrovaných deskových vnitřních sil ve vytvořeném kontrolovaném obvodu v desce.
• Pro posouzení na protlačení se použije maximální hodnota posouvajících sil působících v kontrolovaném obvodu. Tento postup zohledňuje vliv nerovnoměrného rozdělení zatížení. Posouvající síla se pak již součinitelem β nezvyšuje.

Použití maximální hodnoty posouvající síly v základním kontrolovaného obvodu sice představuje nejpřesnější metodu stanovení návrhového zatížení pro protlačení, je ovšem také nejchoulostivější metodou, pokud jde o účinky singularity. Jestliže hodnoty posouvajících sil přebíráme přímo z výpočtu MKP, je třeba obzvlášť dát pozor na to, aby síť konečných prvků v oblasti kontrolované na protlačení byla dostatečně jemná. Pomocí funkce pro zahuštění sítě konečných prvků doporučujeme vytvořit alespoň dva až tři prvky mezi uzlem protlačení a základním kontrolovaným obvodem.

U základů a desek lze posouvající sílu V_Ed redukovat o tlak zeminy v základním kontrolovaném obvodu stanoveném iteračním výpočtem, srov. 6.4.2 (2) [1]. Pokud se v souladu s německou přílohou [2] stanoví u štíhlých základů základní kontrolovaný obvod zjednodušeně ve vzdálenosti 1 d, pak se smí uvažovat pouze 50 % tlaku zeminy. Oba postupy jsou k dispozici v přídavném modulu RF-PUNCH Pro.

Postup při posouzení

Při posouzení na protlačení se nejdříve ověří, zda lze posouzení splnit bez výztuže proti protlačení.

Únosnost ve smyku při protlačení bez smykové výztuže

Únosnost ve smyku při protlačení bez smykové výztuže v_Rd,c se podle 6.4.4 (1), EN 1992-1-1 [1] stanoví následovně:
v_RD,c = C_RD,c ∙ k ∙ (100 ∙ ρ_l ∙ f_ck)^1/3 + k₁ ∙ σ_cp ≥ (v_min + k₁ ∙ σ_cp)
kde
C_Rd,c = 0,18 / γ_c v případě lokálně podepřených desek
C_Rd,c = 0,15 / γ_c v případě desek/základů
k = 1 + √(200 / d)
ρ_l,x/y = A_sl,x/y / (b_w · d_x/y)
ρ_l = √(ρ_l,x ∙ ρ_l,y) ≤ 0,02
A_sl = plocha tahové výztuže
k₁ = 0,1
σ_cp = normálové napětí v základním kontrolovaném obvodu
v_min = 0,035 · k^3/2 · f_ck^1/2

Německá příloha [2] upravuje výše uvedené parametry následovně:
C_Rd,c = 0,18 / γ_c v případě lokálně podepřených desek
C_Rd,c = 0,18 / γ_c ∙ (0,1 ∙ u₀ / d + 0,6) u vnitřních sloupů lokálně podepřených desek, u nichž u₀ / d < 4
C_Rd,c = 0,15 / γ_c v případě desek/základů
ρ_l = √(ρ_l,x ∙ ρ_l,y) ≤ min [0,02;0,5f_cd/f_yd]
v_min = (0,00525 / γ_c) ∙ k^3/2 ∙ f_ck^1/2 pro d ≤ 600 mm
v_min = (0,00375 / γ_c) · k^3/2 · f_ck^1/2 pro d > 800 mm

Posouzení na protlačení je bez přídavné smykové výztuže splněno, pokud v_Ed ≤ v_Rd,c. Vzhledem ke konstrukčně obtížnému provedení smykové výztuže se zpravidla pokoušíme obejít bez smykové výztuže proti protlačení a vystačit s maximálně přípustným stupněm podélného vyztužení ρ_l. V přídavném modulu RF-PUNCH Pro se vypočítá nutný stupeň podélného vyztužení, který umožňuje vynechat smykovou výztuž proti protlačení. Návrhové podélné vyztužení pro výpočet v_Rd,c můžeme ovšem zadat také ručně.

Maximální únosnost ve smyku při protlačení v_Rd,max

Pokud nelze provést posouzení bez smykové výztuže, pak je třeba v dalším kroku prokázat maximální únosnost ve smyku při protlačení v_Rd,max.

Podle 6.4.5 (3), EN 1992-1-1 [1] se maximální únosnost ve smyku při protlačení ověřuje na obvodu sloupu. Uvažovaná délka u₀ obvodu sloupu je afinní k základnímu kontrolovanému obvodu a stanoví se přímo na zatěžované ploše. Maximální únosnost ve smyku při protlačení v_Rd,max na obvodu sloupu se podle 6.4.5.(3), EN 1992-1-1 [1] vypočítá takto:
v_Rd,max = 0,4 · ν ·f_cd
kde ν = 0,6 · (1 - f_ck / 250) (f_ck v [N/mm²])

Působící návrhovou posouvající sílu na obvodu sloupu určíme z následujícího vztahu:
v_Ed,u0 = β · V_Ed / (u₀ · d)

Posouzení je splněno, pokud platí v_{Ed ,u0} ≤ v_Rd,max.

Podle německé národní přílohy [2] se maximální únosnost ve smyku při protlačení neprokazuje na obvodu sloupu, nýbrž v základním kontrolovaném obvodu u1 pomocí rovnice NA6.53.1:
v_Ed,u1 ≤ v_Rd,max = 1,4 · v_Rd,c,u1

Únosnost ve smyku při protlačení se smykovou výztuží

Pokud byl průkaz v_Rd,max proveden úspěšně, pak se v dalším kroku vypočítá nutná smyková výztuž. Nutnou smykovou výztuž stanovíme pomocí upravené rovnice 6.52 z EN 1992‑1‑1 [1]. Nutná výztuž A_sw na jednom obvodu se tak stanoví z výrazu:

kde
v_Rd,c = únosnost ve smyku při protlačení bez smykové výztuže
d = průměrná účinná výška
s_r = radiální vzdálenost obvodů smykové výztuže
f_ywd,ef = 250 + 0,25 d ≤ f_ywd
α = úhel, který svírá smyková výztuž s rovinou desky

Podle DIN EN 1992-1-1/NA [2] se množství výztuže na prvním obvodu zvyšuje součinitelem κ_sw,1 = 2,5 a na druhém obvodu součinitelem κ_sw,2 = 1,4.

Smyková výztuž je uspořádána do vzdálenosti 1,5 d od vnějšího obvodu. Nutná délka u_out,ef vnějšího obvodu se přitom stanoví pomocí rovnice 6.54 z Eurokódu 2 [1]:

Závěr

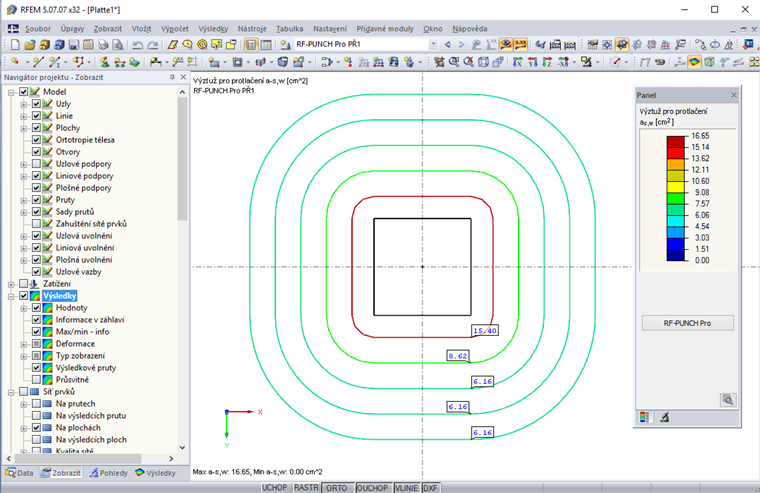
Efektivní posouzení na protlačení podle Eurokódu 2 se neobejde bez softwarového řešení. Příkladem může být výpočet součinitele zvyšujícího zatížení β na modelu s plně plastickým rozdělením posouvající síly v kontrolovaném obvodu nebo iterační stanovení polohy základního kontrolovaného obvodu u základů. Také půdorysy budov mívají stále volnější a složitější provedení, takže nelze pro nedodržení příslušných pravidel uplatňovat případné zjednodušené postupy. Po začlenění přídavného modulu RF-PUNCH Pro do programu RFEM pro výpočty metodou konečných prvků lze veškeré potřebné údaje pro stanovení základního kontrolovaného obvodu i návrhová zatížení pro posouzení na protlačení převzít přímo ze zadání pro výpočet MKP, případně z výpočtu MKP. Posouzení na protlačení v případě sloupů, rohů stěn či konců stěn tak lze provádět velmi efektivně a pohodlně. U sloupů lze zohlednit také rozšířenou sloupovou hlavici. Vyhodnocení výsledků posouzení na protlačení se zobrazí v přehledných tabulkách se všemi nezbytnými mezivýsledky. Výsledky jako nutnou smykovou výztuž, průběh posouvající síly nebo únosnost ve smyku při protlačení lze znázornit také v grafickém okně programu RFEM.

Literatura

[1]	Eurokód 2: Navrhování betonových konstrukcí - Část 1-1: Obecná pravidla a pravidla pro pozemní stavby; ČSN EN 1992-1-1:2006-11
[2]	Nationaler Anhang - National festgelegte Parameter - Eurocode 2: Navrhování betonových konstrukcí - Část 1-1: Allgemeine Bemessungsregeln und Regeln für den Hochbau; DIN EN 1992-1-1/NA:2013-04
[3]	Manuál RFEM 5. Tiefenbach: Dlubal Software, říjen 2014. Stáhnout ...