Cálculo de resistencia a punzonamiento según el Eurocódigo 2 en RFEM

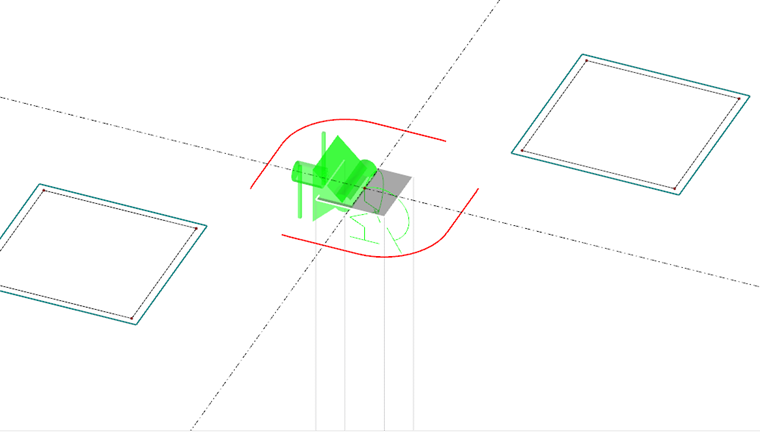
Modelado de la estructura

RFEM 5 le permite realizar el cálculo de punzonamiento tanto para losas 2D como para estructuras 3D. El módulo adicional RF-PUNCH Pro detecta las ubicaciones de la cizalla de punzonado automáticamente y las recomienda para el diseño. Un filtro integrado para encontrar los nudos de punzonamiento se puede configurar individualmente. De esta manera, puede ordenar fácilmente los diseños, por ejemplo, por planos, un esquema de la evidencia, por ejemplo, a los niveles muy fácilmente posibles.

RF-PUNCH Pro reconoce automáticamente el tipo de nodo de punzonado (pilares individuales, extremos de muro o esquinas), así como el área del nodo de punzonado (pilares interiores, de borde o de esquina) del modelo de RFEM.

Perímetro de control básico

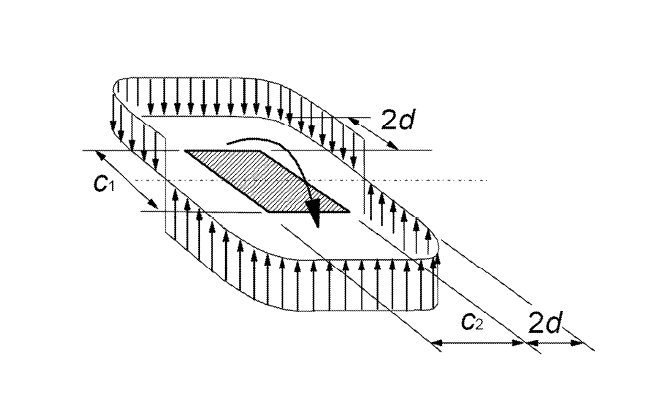
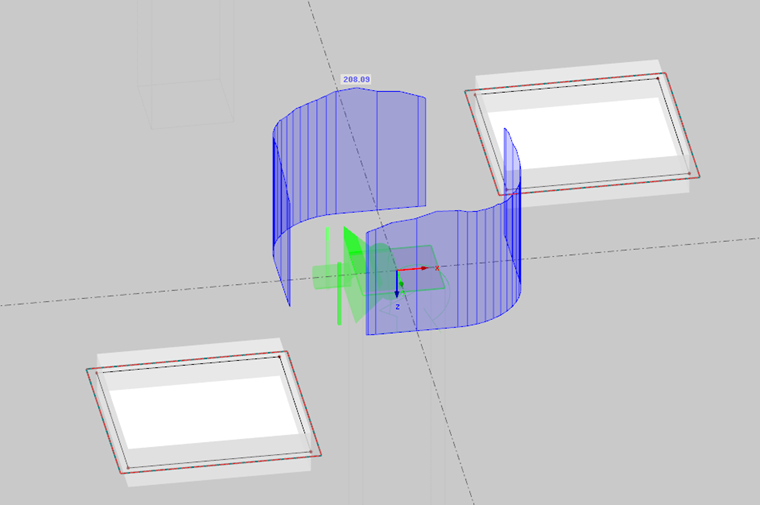
El punzonamiento se realiza en el perímetro de control básico. Según el cap. 6.4.2 de EC 2 [1] , el perímetro de control para losas se encuentra a una distancia de 2 d (d = canto efectivo de la losa) de la superficie de carga. La determinación de la geometría del perímetro de control requiere la consideración de las dimensiones del pilar, así como de las aberturas de la losa hasta la distancia de 6 d de la superficie de carga. RF-PUNCH Pro reconoce automáticamente las aberturas modeladas durante el análisis FEM. Además, también puede definir aberturas más pequeñas en el módulo, que son insignificantes en el cálculo de FEM estructural, por ejemplo. Estos se pueden considerar al determinar el perímetro de control básico. La geometría del perímetro de control se muestra en las ventanas de entrada del módulo adicional incluso antes de iniciar el cálculo.

Kritischer Rundschnitt um eine Stütze unter Berücksichtigung von zwei Öffnungen

En el caso de forjados o cimentaciones, el perímetro crítico suele estar a una distancia de 2 d del borde del pilar. Según 6.4.4 (2) [1], la determinación del perímetro de control requiere un cálculo iterativo. El anexo nacional alemán [2] NCI de 6.4.4 (2) permite un cálculo simplificado para losas de suelo y cimentaciones esbeltas con λ = a_λ/d> 2 (donde a_λ = voladizo de cimentación). En este caso, el perímetro de control se puede establecer a una distancia de 1d. Generalmente, RF-PUNCH Pro realiza un cálculo iterativo para encontrar el perímetro de control de las cimentaciones o losas de piso.

Fuerza cortante relacionada v_Ed

El esfuerzo cortante de cálculo relacionado con el perímetro de control se calcula de acuerdo con la ecuación. 6.38, EC 2 [1]:

Para considerar la carga simétrica rotacional desigual, la carga de punzonado V_Ed se incrementa por el factor de incremento de carga β. Para estructuras rígidamente fijadas donde los vanos adyacentes no difieren en longitud en más del 25%, puede usar los siguientes valores β de acuerdo con EN 1992-1-1, Figura 6.21N [1]:
β = 1,15 para pilares internos
β = 1,4 para pilares de borde
β = 1,5 para pilares de esquina
El anexo alemán [2], figura 6.21N, complementa los factores β con β = 1,35 para las esquinas de los muros y β = 1,2 para los extremos del muro, y especifica el valor recomendado para los pilares internos como β = 1,10.

Un método general para determinar el factor de incremento de carga β se describe en el Eurocódigo 2 [1], Cap. 6.4.3 (3). Aquí, el factor β se determina asumiendo “la distribución de esfuerzos cortantes completamente plásticos en el perímetro de control. De acuerdo con EN 1992-1-1 [1], Eq. (6.39), obtiene:

Distribución de esfuerzos cortantes completamente plástica

Mientras que la expresión (6.39) de EN 1992-1-1 [1] especifica el cálculo de β solo para la excentricidad de la carga uniaxial, el anexo alemán [2] proporciona la expresión ampliada (NA.6.39.1) para considerar la excentricidad de la carga biaxial:

RF-PUNCH Pro incluye las dos opciones para el cálculo de β mencionadas anteriormente. El método estándar es seleccionar el modelo considerando la distribución de esfuerzos cortantes completamente plástica.

RF-PUNCH Pro toma el valor de cálculo del esfuerzo cortante V_Ed directamente del cálculo FEM para realizar el cálculo del cortante por punzonamiento. En el caso del cálculo de cortante por punzonamiento para pilares, apoyos en nudos y cargas concentradas, puede determinar el esfuerzo cortante sobre la base del esfuerzo axial del pilar, el esfuerzo de apoyo o el valor de carga de la fuerza concentrada actuante.

Además, RF-PUNCH Pro le permite crear el perímetro de control en un modelo FEM y determinar allí el esfuerzo cortante activo V_Ed. Para hacer esto, existen las siguientes dos opciones:

• Los esfuerzos cortantes existentes en el perímetro de control se integran o suavizan mediante el mismo perímetro de control. El esfuerzo cortante de cálculo resultante V_Ed debe multiplicarse por el factor de incremento de carga β (véase la ecuación 6.38 [1]). Si el factor β se determina utilizando el modelo de distribución de cortante totalmente plástico, ambos momentos flectores M_{Ed, x} y M_{Ed, y} también se determinan integrando los esfuerzos internos de la losa en el perímetro de control establecido en la losa.
• El valor máximo del esfuerzo cortante existente en el perímetro de control se utiliza para el cálculo de cortante por punzonamiento. Este método tiene en cuenta el efecto de la carga simétrica rotacional desigual utilizando el valor máximo. Por lo tanto, se puede omitir un incremento adicional del esfuerzo cortante por el factor β.

Aunque la utilización del valor máximo de esfuerzo cortante en el perímetro de control es el método más preciso para determinar el valor de cálculo de la carga de punzonado, también es el método más susceptible a los efectos de singularidad. En particular, se debe prestar atención a un refinamiento suficiente de la malla de EF en las áreas de cortante por punzonamiento cuando se toman los esfuerzos cortantes directamente del perímetro de control en el cálculo del FEM. Se recomienda disponer al menos dos o tres elementos entre los nudos de punzonado y el perímetro de control utilizando el refinamiento de la malla de EF.

Distribución de la tensión cortante en la sección

En el caso de cimentaciones y losas de piso, puede reducir V_Ed por la presión del suelo dentro del perímetro de control determinado iterativamente; véase 6.4.2 (2) [1]. Si crea el perímetro de control básico en 1 d para cimentaciones delgadas de acuerdo con el método simplificado del anexo alemán [2], puede aplicar solo el 50% de la presión del suelo. Ambas formas de diseño se pueden seleccionar en RF-PUNCH Pro.

Formulario de diseño

Antes del cálculo de la cizalla de punzonado, el programa comprueba si el cálculo se puede realizar sin punzonar la armadura.

Resistencia al punzonamiento sin armadura de punzonamiento

La resistencia a cortante por punzonamiento sin armadura de cortante v_{Rd, c} debe determinarse según 6.4.4 (1), EN 1992-1-1 [1] de la siguiente manera:
v_{RD, c} = C_{RD, c} ∙ k ∙ (100 ∙ ρ_l ∙ f_ck )^1/3 + k₁ ∙ σ_cp ≥ (v_min + k₁ ∙ σ_cp )
Donde
C_{Rd, c} = 0,18/γ_c para losas planas
C_{Rd, c} = 0,15/γ_c para forjados/cimentaciones
k = 1 + √ (200/d)
ρ_{l, x/y} = A_{sl, x/y}/(b_w · d_x/y )
ρ_l = √ (ρ_{l, x} ∙ ρ_{l, y} ) ≤ 0,02
A_sl = área de la armadura de tracción
k₁ = 0,1
σ_cp = tensión normal en el perímetro de control
v_min = 0,035 · k^3/2 · f_ck^1/2

En el anexo alemán [2], los parámetros mencionados anteriormente se modifican de la siguiente manera:
C_{Rd, c} = 0,18/γ_c para losas planas
C_{Rd, c} = 0,18/γ_c ∙ (0,1 ∙ u₀/d + 0,6) en el caso de pilares interiores de losas planas con u₀/d <4
C_{Rd, c} = 0,15/γ_c para forjados/cimentaciones
ρ_l = √ (ρ_{l, x} ∙ ρ_{l, y} ) ≤ min [0.02; 0.5f_cd/f_yd ]
v_min = (0,00525/γ_c ) ∙ k^3/2 ∙ f_ck^1/2 para d ≤ 600 mm
v_min = (0,00375/γ_c ) · k^3/2 · f_ck^1/2 para d> 800 mm

El cálculo de cortante por punzonamiento se cumple sin refuerzo de punzonado adicional si v_Ed ≤ v_{Rd, c}. Debido al cálculo estructuralmente difícil de la armadura de cortante, generalmente puede intentar evitar el uso de la armadura de punzonado y, en su lugar, aplicar la relación de armadura longitudinal máxima permitida ρ_l para este propósito. RF-PUNCH Pro determina la relación de armadura longitudinal necesaria para evitar la armadura por punzonamiento. Sin embargo, también es posible definir manualmente la armadura longitudinal existente para el cálculo de V_{Rd, c}.

Resistencia máxima al corte por punzonamiento v_{Rd, máx.}

Si el cálculo del cortante por punzonamiento es imposible sin la armadura por punzonamiento, la resistencia máxima al cortante por punzonamiento v_{Rd, max} se calcula en el siguiente paso.

Según 6.4.5 (3) EN 1992-1-1 [1], la resistencia máxima al cortante por punzonamiento se realiza en la periferia de un pilar. La longitud de periferia considerada u₀ encierra el perímetro de control básico y se puede determinar directamente en la superficie de carga. La resistencia máxima al cortante por punzonamiento en la periferia del pilar v_{Rd, max} se determina según 6.4.5. (3), EN 1992-1-1 [1], como sigue:
v_{Rd, máx} = 0,4 · ν · f_cd
donde ν = 0.6 · (1 - f_ck/250) (f_ck en [N/mm²])

El esfuerzo cortante de cálculo activo en la periferia del pilar resulta de:
v_{Ed, u0} = β · V_Ed/(u₀ · d)

El cálculo se cumple si v_{Ed, u0} ≤ v_{Rd, máx}.

En el Anexo Nacional Alemán [2], el cálculo de la resistencia máxima al cortante por punzonamiento no se realiza en la periferia del pilar, sino en el perímetro de control básico u1 según la Expresión NA6.53.1 de la siguiente manera:
v_{Ed, u1} ≤ v_{Rd, máx} = 1,4 · v_{Rd, c, u1}

Resistencia al punzonamiento con refuerzo al punzonamiento

Si el cálculo de v_{Rd, max} se ha realizado con éxito, la armadura de cortante por punzonamiento necesaria se determina en el siguiente paso. La armadura de punzonamiento necesaria se calcula de acuerdo con la Expresión 6.52 ajustada de EN 1992-1-1 [1]. La armadura requerida A_sw resulta de la siguiente ecuación:

Armadura de punzonamiento

Según DIN EN 1992-1-1/NA [2], la cantidad de armadura en el primer perímetro de la armadura de cortante debe incrementarse en el factor κ_{sw, 1} = 2,5, y en κ_{sw, 2} = 1,4 en el segundo cortante perímetro de refuerzo.

La armadura de cortante por punzonamiento debe colocarse a una distancia de 1,5 d desde el perímetro más exterior. La longitud requerida del perímetro más externo es u_{out, ef}, que se define de acuerdo con la ecuación. 6.54 de EC 2 [1]:

Conclusión

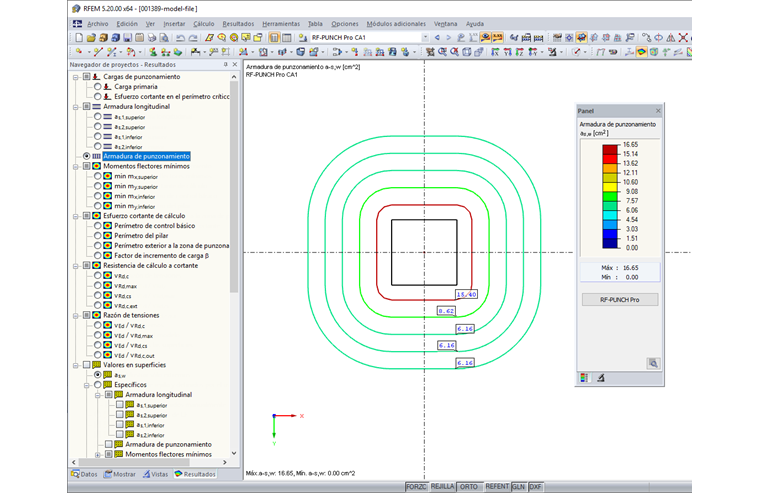
Las disposiciones para el cálculo de la cizalla de punzonado según el Eurocódigo 2 no se pueden aplicar de manera eficiente sin una solución de software. Un ejemplo es el cálculo del factor de incremento de carga β basado en el modelo con distribución del esfuerzo cortante completamente plástico en el perímetro de control, o el cálculo iterativo del área perimetral de control básica de las cimentaciones. Además, los planos de los edificios se diseñan de una manera más libre y compleja, por lo que es imposible seguir las reglas de simplificación; por lo tanto, tampoco se pueden aplicar. El módulo adicional RF-PUNCH Pro del software estructural FEA RFEM le permite tomar todos los datos necesarios para la determinación geométrica del perímetro de control básico y las cargas de cálculo para el cálculo de la cizalla de punzonado directamente desde las entradas FEM o el cálculo FEM. Por lo tanto, el cálculo por punzonamiento de pilares, esquinas de muros y extremos de muros se puede realizar de forma muy sencilla y eficaz. Para las columnas, existe la opción adicional de considerar una cabecera de columna ampliada. Los resultados del cálculo de la cizalla de punzonado se muestran en tablas de resultados claramente ordenadas, incluidos todos los resultados intermedios relevantes para los diseños individuales. Los resultados, así como la armadura de cortante por punzonamiento necesaria, la distribución del esfuerzo cortante y las resistencias de cortante por punzonamiento se pueden mostrar gráficamente en la ventana gráfica de RFEM.

Referencias