确定吊车梁允许变形的方法

基本

对于吊车梁，除了承载能力极限状态外，正常使用极限状态也非常重要。 遵守变形极限值不仅关系到正常使用性，还关系到减少磨损。 因此，大的水平变形会导致吊车的更大的倾斜，从而导致增加的轨道磨损。 此外，还必须尽可能避免竖向变形，以避免起重机在运行过程中振动过大。 最后，还需要限制吊车梁的倾角，否则吊车将无法在满载下移动。

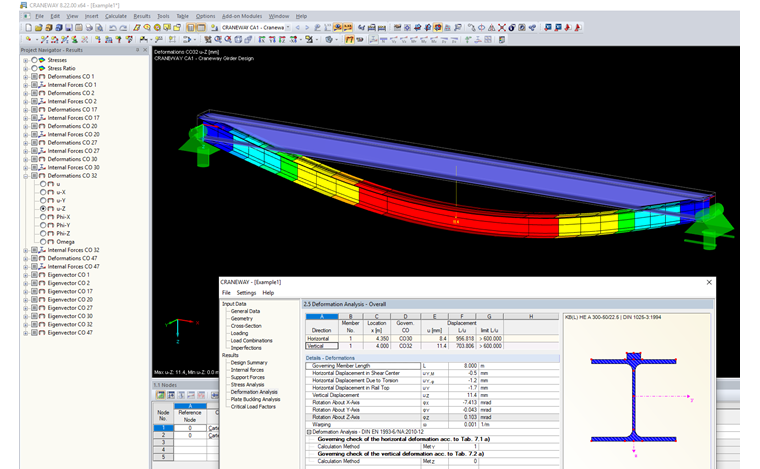
方法 1：变形参照未变形的坐标系

方法 1 适用于有固定支座的简支梁。

适用于以下边界条件：

变形如下：

计算规则为：

1 Maximale vertikale Verformung Kranbahnträger mit starren Auflagern

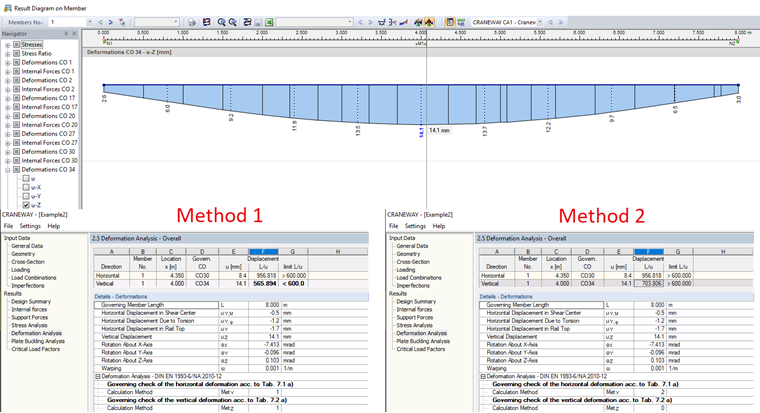
方法 2：变形参照变形体系

如果考虑柔性支座为支座定义弹簧常数，那么可以使用详细信息中的方法 2。 示例文件 2 中包含了为竖向支座定义的弹簧，您可以在本文下方下载该文件。 图02显示了方法1和方法2的区别。

适用于以下边界条件：

变形如下：

计算规则为：

按照这种方法，支座的弹簧刚度也应取大的值。

2 Vergleich der Ergebnisse nach Verfahren 1 und Verfahren 2

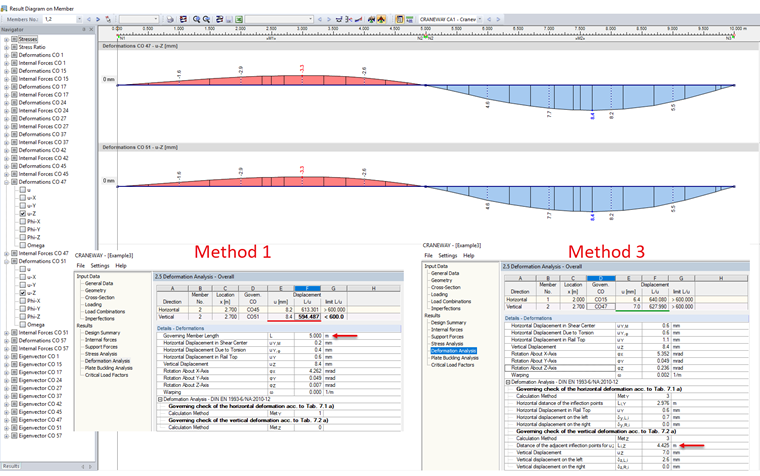
方法 3：变形结构体系的变形相关拐点

该方法适用于连续梁。 与单跨梁相比，在确定多跨梁的容许变形时使用支座间距没有意义。 这会得出保守的、不经济的结果。 为了确定主导长度，在方法 3 中确定受弯线的拐点。

适用于以下条件：

在拐点处：

变形如下：

这种方法的另一个优点是支座可以具有不同的弹簧刚度。

3 Vergleich der Ergebnisse nach Verfahren 1 und Verfahren 3

吊车梁与悬臂梁

对于悬臂梁，弯曲线类似于单跨梁的弯曲线对折。 因此对于方法1，计算如下：

如果激活方法 3，则通过将悬臂梁安装在支座上绕局部坐标轴 y 轴来检查悬臂梁的极限变形。

使用条件为：

方法1的示例文件4的结果悬臂：

方法3的示例文件4的结果悬臂梁：

从图中可以看出，该悬臂梁未达到方法 1 中的容许变形。 然而，在欧洲规范 EN 1993-6 中的附录中表 7.2 a) 行规定了容许垂直变形。

概述总结

为了确保吊车系统正常工作，必须限制变形和位移。 因此也限制了磨损。 如果满足正常使用极限状态设计的极限状态，通常不需要对吊车梁进行振动设计。

知识库

知识库 001612 | 计算吊车跑道梁容许变形的方法