General
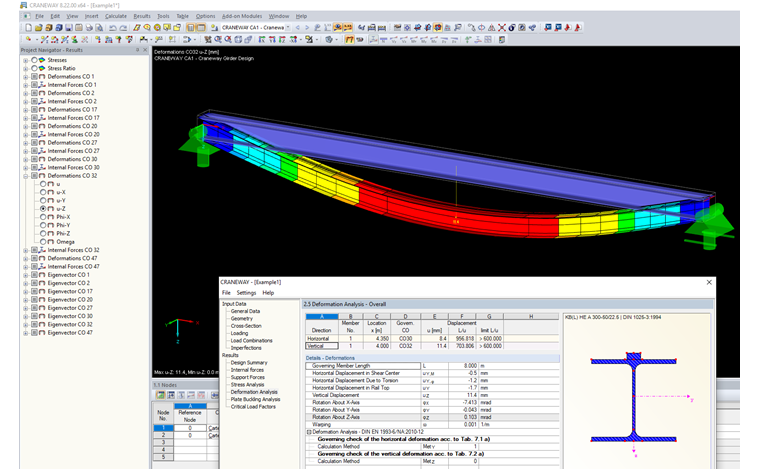
In addition to the ultimate limit state design, the serviceability limit state design is of particular importance for crane runway girders. Compliance with the deformation limit values is important not only for the serviceability, but also for the reduction of wear. Thus, large horizontal deformations can lead to increased skewing of the crane and thus cause increased wear of the tracking means. Vertical deformations must also be avoided to the greatest possible extent in order to avoid excessive vibration of the crane during operation. Finally, it is also necessary to limit the inclination (slope) of the crane runway girder, because otherwise the crane will not be able to move under full load.
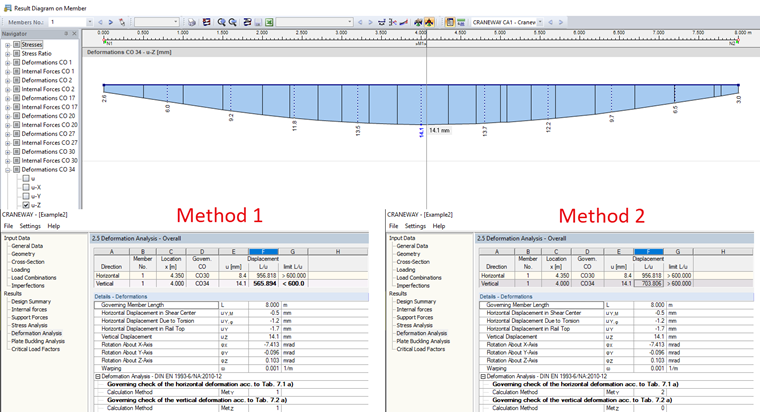
Method 1: Deformation Related to Undeformed System
Method 1 can be used for single-span beams with fixed and rigid supports.
The following boundary conditions apply:
The deformation is determined as follows:
|
Uc |
Cross-section deformation |
|
UL |
Deformation of the left support |
|
UR |
Deformation of the right support |
|
x |
Coordinate of the cross-section in the local axis system |
|
L |
Distance of supports |
The rule is:
Method 2: Deformation Related to Deformed Structural System
If you define spring constants for the supports to consider flexible supports, you can use Method 2 under Details. Example File 2, which you can download below this article, contains defined springs for the vertical supports. Image 02 shows the difference between Method 1 and Method 2.
The following boundary conditions apply:
The deformation is determined as follows:
|
Uc |
Cross-section deformation |
|
UL |
Deformation of the left support |
|
UR |
Deformation of the right support |
|
x |
Coordinate of the cross-section in the local axis system |
|
L |
Distance of supports |
The rule is:
The spring stiffnesses of the supports should have similarly large values when using this method.
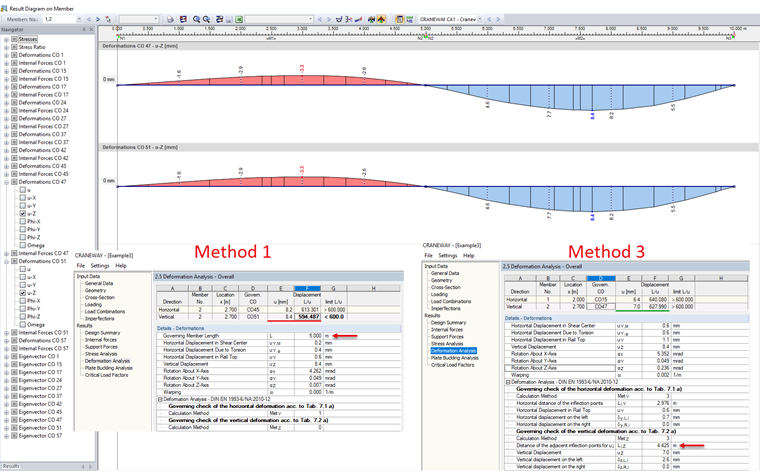
Method 3: Deformation Related Inflection Points of Deformed Structural System
This method is used for continuous beams. Compared to a single-span beam, it does not make sense to use the distance between the supports to determine the allowable deformation for multi-span beams. This can lead to conservative, uneconomical results. In order to determine the governing length, the inflection points of the bending line are determined in Method 3.
The following condition is applied:
At the inflection points:
The deformation is determined as follows:
|
Uc |
Deformation of the cross-section |
|
ULi |
Deformation of the left inflection point |
|
URi |
Deformation of the right inflection point |
|
x |
Coordinate of the cross-section in the local axis system |
|
L |
Distance between the left and right inflection points |
Another advantage of this method is that the supports can also have different spring stiffnesses.
Crane Runway Girder with Cantilevers
For cantilevers, the bending line is similar to the half-inverted bending line of a single-span beam. Therefore, the following calculation is performed for Method 1:
If Method 3 is activated, the limit deformation of a cantilever is checked by rotating the cantilever on the support around the local y-axis.
The limit condition is as follows:
Result cantilever of Example File 4 with Method 1:
→ not fulfilled
In other words:
Result cantilever of Example File 4 with Method 3:
You can see that the allowable deformation according to Method 1 for the cantilever has not been met. However, the German National Annex to EN 1993-6 specifies
for the allowable vertical deformation according to Table 7.2 row a).Conclusion
To ensure the correct functioning of a crane system, deformations and displacements must be limited. As a result, the wear is also limited. If the limit conditions of the serviceability limit state design are met, it is usually unnecessary to carry out a separate vibration design for the crane runway girder.