8536x

001612

Dipl.-Ing. (FH) René Flori

03.12.2019

Méthode pour déterminer les déformations admissibles d'un chemin de roulement

Cet article décrit les différentes options pour déterminer les déformations admissibles d'un chemin de roulement. Il est nécessaire de définir clairement la méthode adéquate car ce sont des poutres à travées multiples et des appuis latéraux semi-rigides (contreventements en acier) qui sont utilisés dans la pratique.

Général

Les vérifications à l'ELU et à l'ELS sont particulièrement importantes dans le cas de chemins de roulement. Les valeurs limites de déformation doivent être respectées car elles sont importantes pour l'état limite de service, mais également pour la réduction de l'usure. De grandes déformations horizontales peuvent ainsi provoquer une inclinaison accrue du pont roulant et accentuer l'usure des dispositifs de guidage. Les déformations verticales doivent également être évitées autant que possible afin que la grue ne soit pas sujette à des vibrations excessives lorsqu'elle est en fonctionnement. Enfin, il est également nécessaire de limiter l'inclinaison (pente) du chemin de roulement ou la grue ne pourra pas se déplacer à pleine charge.

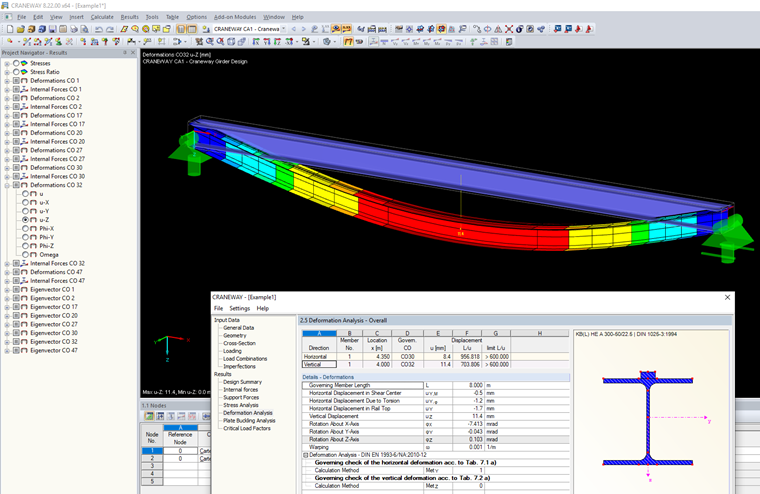
Méthode 1 : déformation rapportée au système non déformé

La méthode 1 peut être utilisée pour les poutres à travée simple avec appuis fixes et rigides.

Les conditions limites suivantes sont appliquées :

δ_{y, z} < \frac{L}{X} oder δ_{y, z} < 25 mm

Conditions aux limites pour les déformations

La déformation est déterminée comme suit :

δ_{y, z} = |\frac{U_{c} - U_{L} - (U_{R} - U_{L}) \cdot x}{L}| < \frac{L}{X}

U_c	déformation de la section
U_L	déformation de l'appui gauche
U_r	Déformation de l'appui droit
x	coordonnées de la section dans le système d'axes local
L	distance des appuis

déformation

Ce qui suit s'applique :

U_{c} \neq 0, U_{L} = 0, U_{R} = 0

Conditions pour l'option 1

1 Déformation verticale maximale d'un chemin de roulements avec des appuis rigides

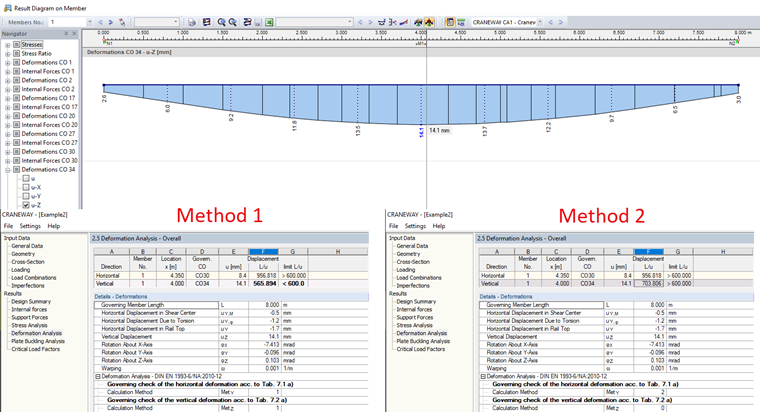
Méthode 2 : déformations rapportées au système déformé

Si des constantes de ressort sont définies pour considérer des appuis flexibles, cette méthode 2 est disponible dans Détails. Dans l'exemple du fichier 2, des ressorts ont été définis pour les appuis verticaux. La Figure 02 montre les différences entre la Méthode 1 et la Méthode 2.

Les conditions limites suivantes sont appliquées :

δ_{y, z} < \frac{L}{X} oder δ_{y, z} < 25 mm

Conditions aux limites pour les déformations

La déformation est déterminée comme suit :

δ_{y, z} = |\frac{U_{c} - U_{L} - (U_{R} - U_{L}) \cdot x}{L}| < \frac{L}{X}

U_c	déformation de la section
U_L	déformation de l'appui gauche
U_r	Déformation de l'appui droit
x	coordonnées de la section dans le système d'axes local
L	distance des appuis

déformation

Ce qui suit s'applique :

U_{c} \neq 0, U_{L} \neq 0, U_{R} \neq 0

Conditions pour l'option 2

Les rigidités de ressort des appuis doivent avoir des valeurs élevées si cette méthode est utilisée.

2 Comparaison des résultats selon la méthode 1 et la méthode 2

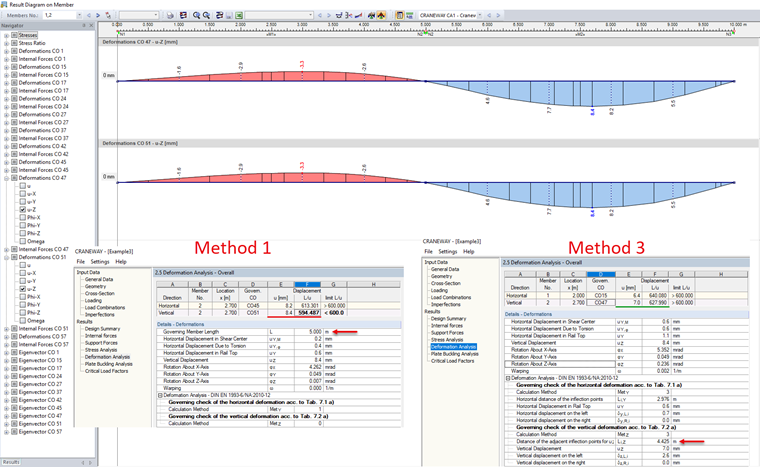
Méthode 3 : déformations rapportées aux points d'inflexion du système déformé

Cette méthode est utilisée pour les poutres continues. Contrairement au cas d'une poutre à travée simple, il n'est pas judicieux d'utiliser la distance des appuis pour déterminer la déformation admissible des poutres à travées multiples. Cette méthode générerait en effet des résultats trop coûteux. Les points d'inflexion de la ligne de flexion sont déterminés selon la Méthode 3 pour obtenir la longueur déterminante.

La condition suivante est appliquée :

ω'' = - \frac{M_{y}}{E \cdot I_{y}}

Points d'inflexion de la ligne de flexion

Aux points d'inflexion :

ω'' = 0

Condition pour les points d'inflexion

La déformation est déterminée comme suit :

δ_{y, z} = |\frac{U_{c} - U_{Li} - (U_{Ri} - U_{Li}) \cdot x}{L}| < \frac{L}{X}

U_c	déformation de la section
U_Li	déformation du point d'inflexion gauche
U_Ri	déformation du point d'inflexion droit
x	coordonnées de la section dans le système d'axes local
L	distance entre les points de flexion gauche et droit

déformation

Cette méthode offre un autre avantage : les appuis peuvent également avoir différentes rigidités de ressort.

3 Comparaison des résultats selon la méthode 1 et la méthode 3

Chemin de roulement avec porte-à-faux

La ligne de flexion des porte-à-faux est similaire à la ligne de flexion à moitié inversée d'une poutre à travée simple. Par conséquent, le calcul suivant est effectué pour la Méthode 1 :

δ_{y, z} = |U_{c}| < 2 \cdot \frac{L}{X}

Calcul des porte-à-faux pour la méthode 1

Si la Méthode 3 est utilisée, la déformation limite d'un porte-à-faux est vérifiée en le faisant tourner sur le support autour de l'axe y local.

La condition limite est la suivante :

φ_{y} < \frac{1}{200}

Condition aux limites

Résultats du porte-à-faux du fichier d'exemple 4 selon la méthode 1 :

δ_{z} = |7.618 mm| < 2 \cdot \frac{2000}{600}

δ_{z} = |7.618 mm| < 6.667

Calcul des déformations du porte-à-faux selon la méthode 1

→ non remplie
Autrement dit :

\frac{7.618}{2 \cdot 2000} = 525 > 600

Calcul avec la méthode 1

Résultats du porte-à-faux du fichier d'exemple 4 selon la méthode 1 :

φ_{y} = 4.258 mrad = 0.004258 rad < \frac{1}{200} rad

0.004258 < 0.005 \to OK

\frac{0.004258}{0.005} = 0.851 < 1

Calcul des déformations du porte-à-faux selon la méthode 3

Il apparaît que la déformation admissible selon la méthode 1 n'est pas respectée pour le porte-à-faux. Toutefois, l'Annexe Nationale allemande de l'EN 1993-6 fournit la déformation verticale admissible selon le Tableau 7.2, ligne a).

δ_{y, z} < \frac{L}{500} und δ_{y, z} \leq 25 mm

Déformation verticale admissible selon DIN EN 1993-6

entre autres.

Conclusion

Les déformations et les déplacements doivent être limités pour garantir le bon fonctionnement d'un système de chemin de roulements, ce qui permet en outre de limiter l'usure. Si les conditions limites de vérification à l'ELS sont remplies, il n'est généralement pas nécessaire d'effectuer une vérification distincte des vibrations pour le chemin de roulement.