Ogólne informacje
Oprócz obliczeń stanu granicznego nośności, obliczanie stanu granicznego użytkowalności ma szczególne znaczenie dla belek podsuwnicowych. Zgodność z wartościami granicznymi odkształceń jest istotna nie tylko dla użytkowalności, ale także dla ograniczenia zużycia. Tym samym duże odkształcenia poziome mogą prowadzić do zwiększonego pochylania żurawia, a tym samym powodować większe zużycie elementów prowadnicy. Należy również w jak największym stopniu uniknąć odkształceń pionowych, aby uniknąć nadmiernych drgań żurawia podczas pracy. Wreszcie, konieczne jest również ograniczenie nachylenia (nachylenia) belki podsuwnicowej żurawia, gdyż w przeciwnym razie żuraw nie będzie mógł poruszać się pod pełnym obciążeniem.
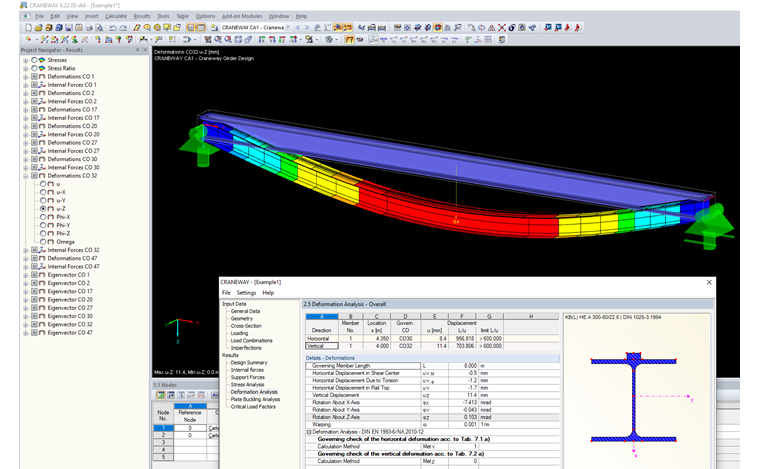
Metoda 1: Deformacje odnoszące się do nieodkształconego układu
Metoda 1 może być stosowana do belek jednoprzęsłowych o podporach sztywnych i przegubowych.
Obowiązują następujące warunki brzegowe:
Odkształcenie jest określane w następujący sposób:
uC... Odkształcenie przekroju
UL... Odkształcenie lewej podpory
UR... Odkształcenie prawej podpory
x ... Współrzędna przekroju w lokalnym układzie osi
L ... Odległość między podporami
Obowiązują poniższe zależności:
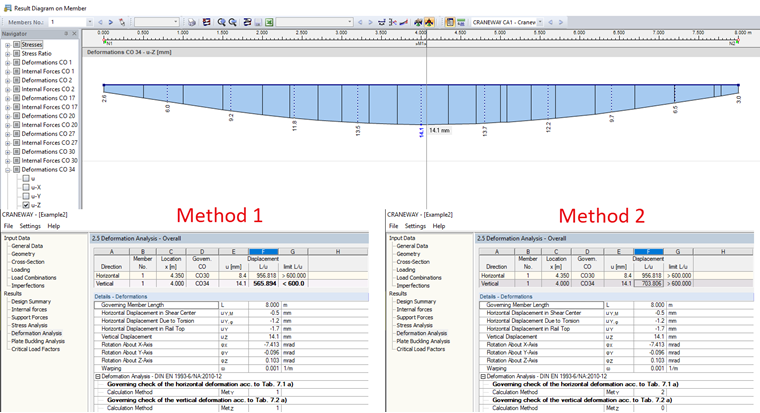
Metoda 2: Deformacje odnoszące się do odkształconego układu
W przypadku zastosowania podpór o zdefiniowanej sprężystości można zastosować metodę 2 w sekcji Szczegóły. Przykładowy plik 2, który dostępny jest do pobrania pod niniejszym artykułem zawiera zdefiniowane sprężystości dla podpór pionowych Rysunek 02 pokazuje różnicę pomiędzy metodą 1 a metodą 2.
Obowiązują następujące warunki brzegowe:
Odkształcenie jest określane w następujący sposób:
Obowiązują poniższe zależności:
W przypadku stosowania tej metody sztywności sprężystych podpór powinny mieć ten sam rząd wielkości.
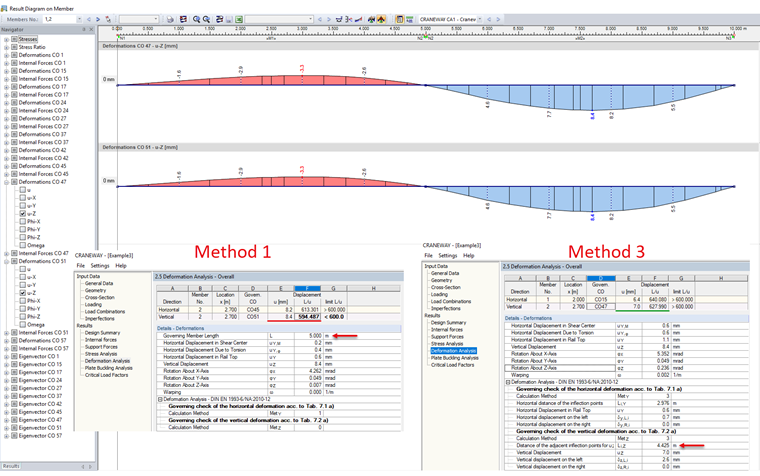
Metoda 3: Deformacje odnoszące się do punktów stycznych odkształconego układu
Metoda ta jest stosowana dla belek ciągłych. W przeciwieństwie do belek jednoprzęsłowych, w przypadku belek ciągłych wykorzystywanie odległości między podporami do określania dopuszczalnego odkształcenia jest nieuzasadnione. Może to prowadzić do konserwatywnych, nieekonomicznych wyników. W celu określenia długości miarodajnej do sprawdzenia ugięć,j punkty przegięcia linii zginania są określane zgodnie z metodą 3.
Zastosowany jest następujący warunek:
W punktach przegięcia:
Odkształcenie jest określane w następujący sposób:
uC... Odkształcenie przekroju
ULi... Odkształcenie lewego punktu przegięcia
URi... Odkształcenie prawego punktu przegięcia
x ... Współrzędna przekroju w lokalnym układzie osi
L ... Odległość pomiędzy lewym i prawym punktem przegięcia
Kolejną zaletą tej metody jest też to, że podporom można przypisać różne sprężystości.
Belki podsuwnicowe ze wspornikami
W przypadku wsporników linia zginania jest podobna do odwróconej połówki linii zginania belki jednoprzęsłowej. Dlatego dla metody 1 przeprowadza się następujące wyliczenie:
Jeżeli Metoda 3 jest aktywna, graniczne odkształcenie wspornika jest sprawdzane poprzez obrót wspornika na podporze wokół lokalnej osi y.
Warunek graniczny jest następujący:
Wyniki dla wspornika z pliku przykładowego 4 - Metoda 1:
Wyniki dla wspornika z pliku przykładowego 4 - Metoda 3:
Jak widać, dopuszczalne odkształcenie wspornika według Metody 1 nie zostało spełnione. Jednak niemiecki załącznik krajowy do EN 1993-6 określa
jako dopuszczalne odkształcenie pionowe zgodnie z tabelą 7.2, wiersz a).Podsumowanie
Aby zapewnić prawidłowe funkcjonowanie suwnicy, odkształcenia i przemieszczenia muszą być ograniczone. W rezultacie ograniczone jest także zużycie. Jeżeli zostaną spełnione warunki graniczne stanu granicznego użytkowalności, zazwyczaj nie ma potrzeby przeprowadzania dodatkowej analizy dynamicznej belki podsuwnicowej.
Dlubal_KohlA_]_LI.jpg?mw=350&hash=21d94ec9a723c608496e9e95a21bb1309ab5067a)
.png?mw=350&hash=2b12ead9717e0abbf1c0c14bba66b0a2adcaed73)
DIN EN 1993-6/NA: 2010-12 (Niemcy) 
NBN EN 1993-6/ANB: 2011-03 (Belgia) 
SFS EN 1993-6/NA: 2010-03 (Finlandia) 
NF EN 1993-6/NA: 2011-12 (Francja) 
UNI EN 1993-6/NA: 2011-02 (Włochy) 
LST EN 1993-6/NA: 2010-12 (Litwa) 
NEN EN 1993-6/NB: 2012-05 (Holandia) 
NS EN 1993-6/NA: 2010-01 (Norwegia) 
SS EN 1993-6/NA: 2011-04 (Szwecja) 
CSN EN 1993-6/NA: 2010-03 (Republika Czeska) 
BS EN 1993-6/NA: 2009-11 (Wielka Brytania) 
CYS EN 1993-6/NA: 2009-03 (Cypr) 
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
