8652x

001612

Dipl.-Ing. (FH) René Flori

3.12.2019

Metody stanovení přípustné deformace nosníků jeřábových drah

V tomto příspěvku popíšeme různé možnosti, jak stanovit přípustnou deformaci nosníků jeřábové dráhy. Vzhledem k tomu, že se v praxi používají nosníky o několika polích a poddajné příčné podpory (podélné ztužení), chceme v našem příspěvku objasnit, jak vybrat správnou metodu.

Obecné

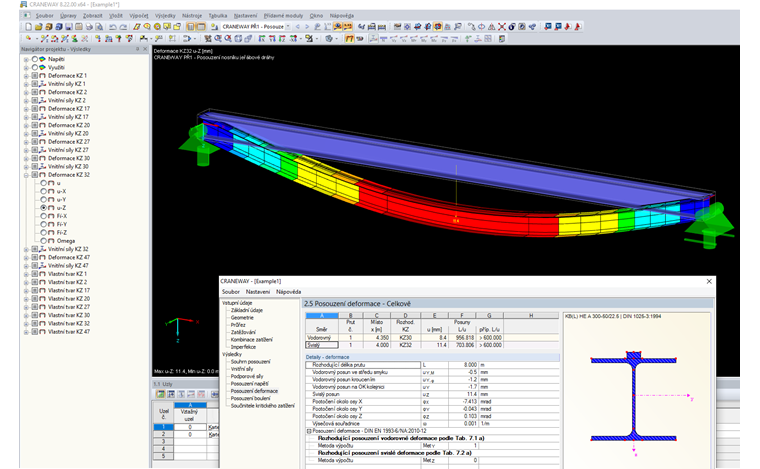
Kromě posouzení mezního stavu únosnosti je u nosníků jeřábových drah obzvlášť důležité také posouzení mezního stavu použitelnosti. Dodržení mezních hodnot deformace není důležité pouze pro použitelnost, ale také pro omezení opotřebení. Velké vodorovné deformace mohou vést ke zvýšenému příčení jeřábu, a tím i k většímu opotřebení vodicích prostředků. Také je třeba se v co největší míře vyvarovat svislým deformacím, aby se vyloučily nadměrné vibrace při provozu jeřábu. A konečně je také třeba omezit sklon nosníku jeřábové dráhy, protože v opačném případě nelze zajistit pohyb jeřábu při plném zatížení.

Metoda 1: Deformace vztažená na nedeformovaný systém

U nosníků o jednom poli s neposuvnými tuhými podporami lze použít metodu 1.

Platí přitom následující okrajové podmínky:

δ_{y, z} < \frac{L}{X} oder δ_{y, z} < 25 mm

Okrajové podmínky pro deformaci

Deformace se stanoví následovně:

δ_{y, z} = |\frac{U_{c} - U_{L} - (U_{R} - U_{L}) \cdot x}{L}| < \frac{L}{X}

U_c	deformace průřezu
U_L	deformace levé podpory
U_R	deformace pravé podpory
x	souřadnice průřezu v lokálním osovém systému
L	vzdálenost podpor

Deformace

Přitom platí:

U_{c} \neq 0, U_{L} = 0, U_{R} = 0

Podmínky pro variantu 1

1 Maximale vertikale Verformung Kranbahnträger mit starren Auflagern

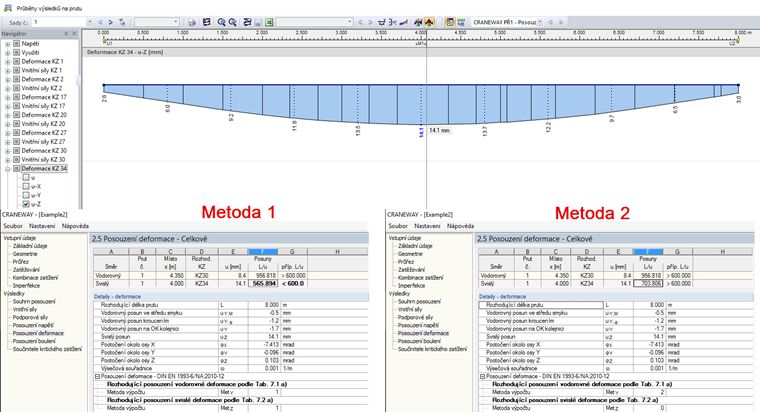
Metoda 2: Deformace vztažená na deformovaný systém

Pokud pro zohlednění poddajných podpor definujeme konstanty tuhosti, budeme mít v Detailech k dispozici metodu 2. V příkladu 2, jehož soubor připojujeme k tomuto článku, jsme zadali konstanty tuhosti pro svislé podpory. Rozdíl mezi metodou 1 a metodou 2 je znázorněn na obr. 02.

Platí přitom následující okrajové podmínky:

δ_{y, z} < \frac{L}{X} oder δ_{y, z} < 25 mm

Okrajové podmínky pro deformaci

Deformace se stanoví následovně:

δ_{y, z} = |\frac{U_{c} - U_{L} - (U_{R} - U_{L}) \cdot x}{L}| < \frac{L}{X}

U_c	deformace průřezu
U_L	deformace levé podpory
U_R	deformace pravé podpory
x	souřadnice průřezu v lokálním osovém systému
L	vzdálenost podpor

Deformace

Přitom platí:

U_{c} \neq 0, U_{L} \neq 0, U_{R} \neq 0

Podmínky pro variantu 2

Při použití této metody by měly podpory vykazovat podobné hodnoty tuhosti.

2 Vergleich der Ergebnisse nach Verfahren 1 und Verfahren 2

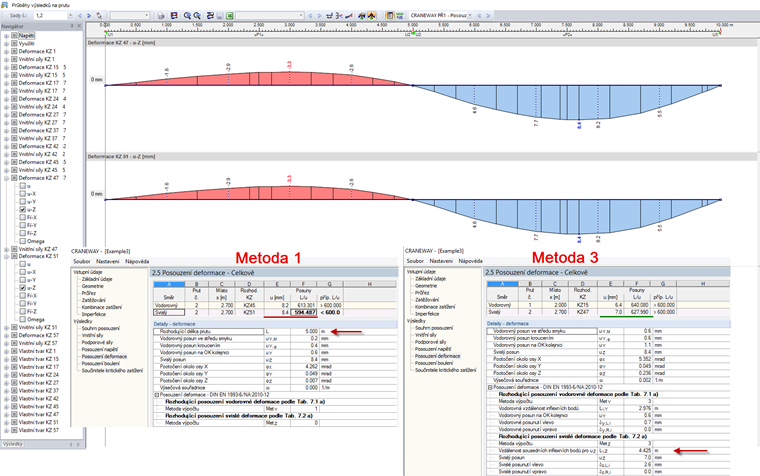
Metoda 3: Deformace vztažená na inflexní body deformovaného systému

Tato metoda se používá u spojitých nosníků. Oproti nosníku o jednom poli není u nosníku o několika polích vhodné vycházet při stanovení přípustné deformace ze vzdálenosti podpor. Může to vést ke konzervativním, nehospodárným výsledkům. Pro určení rozhodující délky se při použití metody 3 stanoví inflexní body ohybové křivky.

Použije se následující podmínka:

ω'' = - \frac{M_{y}}{E \cdot I_{y}}

Inflexní body linie ohybu

V inflexních bodech platí:

ω'' = 0

Podmínka pro inflexní body

Deformace se stanoví následovně:

δ_{y, z} = |\frac{U_{c} - U_{Li} - (U_{Ri} - U_{Li}) \cdot x}{L}| < \frac{L}{X}

U_c	deformace průřezu
U_Li	deformace levého inflexního bodu
U_Ri	deformace pravého inflexního bodu
x	souřadnice průřezu v lokálním osovém systému
L	vzdálenost mezi levým a pravým inflexním bodem

Deformace

Další výhodou této metody je, že podpory mohou mít také různé tuhosti.

3 Vergleich der Ergebnisse nach Verfahren 1 und Verfahren 3

Nosník jeřábové dráhy s konzolami

U konzol se ohybová křivka podobá poloviční převrácené ohybové křivce nosníku o jednom poli. Při použití metody 1 tak výpočet vypadá následovně:

δ_{y, z} = |U_{c}| < 2 \cdot \frac{L}{X}

Výpočet pro konzoly pro metodu 1

Pokud se aktivuje metoda 3, pak se mezní deformace konzoly ověří na základě pootočení konzoly na podpoře okolo lokální osy y.

Platí přitom následující mezní podmínka:

φ_{y} < \frac{1}{200}

Okrajová podmínka

Výsledky pro konzolu v příkladu 4 při použití metody 1:

δ_{z} = |7.618 mm| < 2 \cdot \frac{2000}{600}

δ_{z} = |7.618 mm| < 6.667

Výpočet deformace konzoly metodou 1

→ Nesplněno
Jinými slovy:

\frac{7.618}{2 \cdot 2000} = 525 > 600

Výpočet metodou 1

Výsledky pro konzolu v příkladu 4 při použití metody 3:

φ_{y} = 4.258 mrad = 0.004258 rad < \frac{1}{200} rad

0.004258 < 0.005 \to OK

\frac{0.004258}{0.005} = 0.851 < 1

Výpočet deformace konzoly metodou 3

Jak vidíme, přípustná deformace není při výpočtu metodou 1 u konzoly dodržena. Německá národní příloha k EN 1993-6 však stanoví přípustnou svislou deformaci podle tabulky 7.2, řádek a).

δ_{y, z} < \frac{L}{500} und δ_{y, z} \leq 25 mm

Přípustná svislá deformace podle DIN EN 1993-6

kteří mají zájem spolupracovat.

Závěr a výhled

Pro zajištění bezvadného provozu jeřábového systému je třeba omezit průhyby a posuny. Tím se rovněž omezí opotřebení. Pokud jsou splněny mezní podmínky při posouzení mezního stavu použitelnosti, nemusí se zpravidla u nosníku jeřábové dráhy provést samostatné posouzení na vibrace.