按 2014 CSA 标准的木梁设计

木梁分析

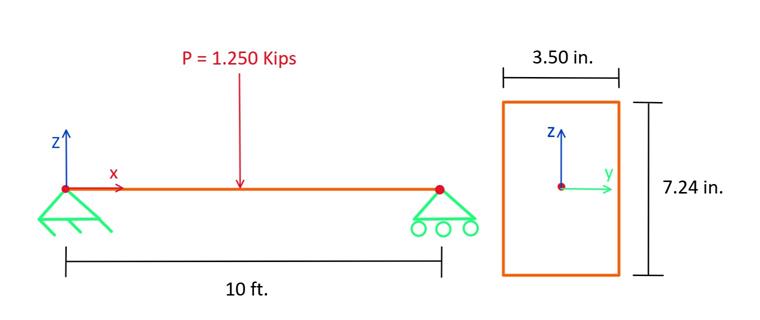
设计一根跨度10英尺、名义尺寸为38 mm × 89 mm的支承在简支梁上的道格拉斯杉-落叶松结构梁（DF-L SS），在中跨加载1.250 kip的点载荷。此分析的目的是确定梁的调整弯曲因子和弯矩抗力。假设为长期载荷持续时间。此示例中的负载标准已简化。典型的负载组合可以参考第5.2.4节 [1]。在图像01中，显示了带有载荷和尺寸的简支梁的图示。

1 Trägerbelastung und Maßangaben

梁属性

此示例中使用的截面为89 mm × 184 mm名义尺寸木材。锯材梁的实际截面属性计算如下：

• b = 3.50 英寸, d = 7.24 英寸, L = 10 英尺
• 总截面面积：
  $${\mathrm{A}}_{\mathrm{g}} = \mathrm{b} \cdot \mathrm{d} = (3.50 \mathrm{in}) \cdot (7.24 \mathrm{in}) = 25.34 \mathrm{in}²$$

  总截面面积
• 截面模量：
  $${\mathrm{S}}_{\mathrm{x}} = \frac{\mathrm{b} · {\mathrm{d}}^2}{6} = \frac{(3.50 \mathrm{in}) · {(7.24 \mathrm{in})}^2}{6} = 30.58 {\mathrm{in}}^3$$

  截面模量
• 惯性矩：
  $${\mathrm{I}}_{\mathrm{x}} = \frac{\mathrm{b} · {\mathrm{d}}^3}{12} = \frac{(3.50 \mathrm{in}) · {(7.24 \mathrm{in})}^3}{12} = 110.69 {\mathrm{in}}^4$$

  惯性矩

此示例中使用的材料为DF-L SS。材料属性如下。

• 参考弯曲设计值：f_b = 2,393.12 psi
• 弹性模量：E = 1,812,970 psi

梁修正系数

根据CSA O86-14标准设计木构件时，必须对参考的弯曲设计值（f_b）应用修正系数。最终将提供调整的弯曲设计值（F_b）以及分系数弯矩抗力（M_r）。

以下进一步解释和确定本示例中的每个修正系数。

K_D

载荷持续时间系数考虑了不同的载荷周期。雪、风和地震荷载都用K_D考虑。这意味着K_D依赖于负载情况。在本例中，根据表5.3.2.2 [1], 假设为长期载荷持续时间，K_D设为0.65。

K_S

湿度服务系数考虑了锯材的干湿服务条件以及截面尺寸。对于此示例，我们假设纤维极限的弯曲和湿服务条件。根据表6.4.2 [1], K_s等于0.84。

K_T

处理调整系数考虑了经过阻燃或其他降低强度的化学处理过的木材。此系数由基于文献的时间、温度和湿度测试的强度和刚度能力测定。对于此系数，参考第6.4.3节 [1]。在此示例中，弹性模量乘以0.95，其他所有属性乘以0.85，假设为湿服务条件。

K_Z

尺寸系数考虑了木材的不同尺寸以及荷载如何施加到梁上。有关此系数的更多信息，请参见第6.4.5节 [1]。在此示例中，基于尺寸、弯曲和剪切以及表6.4.5 [1]，K_Z等于1.30。

K_H

系统系数考虑三种或更多平行的锯材构件。这些构件之间的间隔不得超过610 mm，并且必须共同支撑载荷。此标准在第6.4.4节定义为案例1 [1]。对于此示例，根据表6.4.4，每个弯曲构件在案例1中，K_H = 1.10。

K_L

侧向稳定因子考虑沿构件长度提供的侧向支撑，这有助于防止侧向位移和旋转。侧向稳定因子（K_L）计算如下。

分系数指定弯曲强度 (F_B)

下面的部分确定分系数指定弯曲强度（F_b）。通过将指定的弯曲强度（f_b）与以下修正系数相乘计算F_b。

• K_D = 0.65
• K_H = 1.10
• K_s = 0.84
• K_T = 0.85

我们现在可以使用第6.5.4.1节中的以下方程计算F_b [1]。

侧向稳定因子, K_L

侧向稳定因子（K_L）从第6.5.4.2节计算 [1]。在可以确定K_L之前，必须计算苗条系数。首先，在表7.5.6.4.3 [1]中找到有效长度（L_e）。对于此梁示例，在中心施加集中载荷，没有中间支撑。无支撑长度（l_u）为10英尺。

• L_e = 1.61 (l_u)
• L_e = 16.10 英尺

然后，根据第7.5.6.4.3节计算苗条系数（C_B） [1]。

由于苗条系数大于10，C_k应计算。参考第6.4.2节，K_SE等于0.94。

C_B小于C_k，因此我们可以根据第7.5.6.4 (b) 节计算K_L [1]。

梁设计比例

此示例的最终目标是获得此简单梁的设计比例。这将决定在给定负载下构件尺寸是否合适，或是否需要进一步优化。计算设计比例需要分系数弯矩抗力（M_r）和分系数弯矩（M_f）。

沿x轴的最大弯矩（M_f）通过以下公式确定：

接下来，可以根据第6.5.4.1节计算分系数弯矩抗力（M_r） [1]。 M_r = 0.90 ⋅ F_b ⋅ S ⋅ K_z ⋅ K_L M_r = 3.63 kip ⋅ ft

最后，现在可以计算设计比例（η）。

在RFEM中的应用

对于符合CSA O86-14标准的木材设计，在RFEM中，附加模块RF-TIMBER CSA根据载荷标准和构件能力分析和优化截面，适用于单个构件或构件组。在RF-TIMBER CSA中建模和设计上述梁示例时，可以比较结果。

2 RFEM-Modell

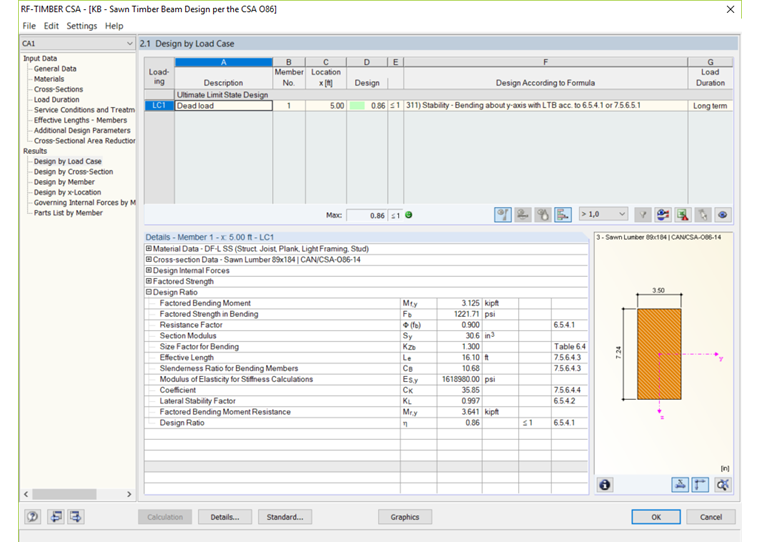
在RF-TIMBER AWC附加模块的常规数据表中，选择构件、载荷条件和设计方法。材料和截面从RFEM中定义，负载持续时间设定为长期。湿度服务条件设为湿处理设为防腐（刻痕）。有效长度（L_e）从表7.5.6.4.3中确定 [1]。模块计算得出分系数弯矩（M_f）为3.125 kip ⋅ ft和分系数弯矩抗力（M_r）为3.641 kip ⋅ ft。从这些值确定的设计比例（η）为0.86，与上述分析手算结果非常接近。

3 附加模块 RF-TIMBER CSA