Timber Beam Design as per 2014 CSA Standard

Timber Beam Analysis

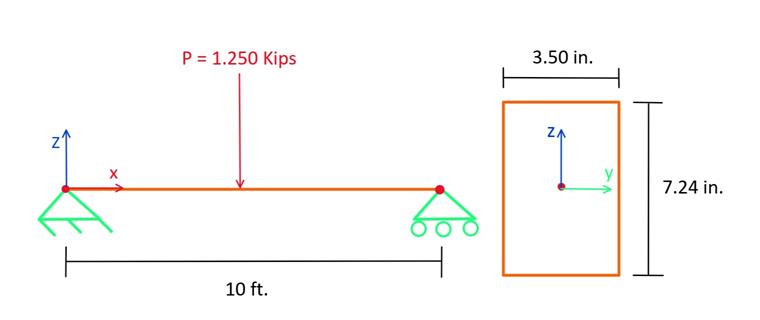
A simply supported 10-foot-long, nominal 38 mm ⋅ 89 mm Douglas Fir-Larch Structural (DF-L SS) beam with a mid-span point load of 1.250 kips will be designed. The goal of this analysis is to determine the adjusted bending factors and moment resistance of the beam. A long-term load duration is assumed. The loading criteria are simplified for this example. Typical load combinations can be referenced in Sec. 5.2.4 [1]. In Image 01, a diagram of the simple beam with loads and dimensions is shown.

1 Beam Loading and Dimensions

Beam Properties

The cross-section used in this example is a 89 mm ⋅ 184 mm nominal dimension lumber. The actual cross-section property calculations of the sawn timber beam can be viewed below:

• b = 3.50 in, d = 7.24 in, L = 10 ft
• Gross cross-section area:
  $${\mathrm{A}}_{\mathrm{g}} = \mathrm{b} \cdot \mathrm{d} = (3.50 \mathrm{in}) \cdot (7.24 \mathrm{in}) = 25.34 \mathrm{in}²$$

  Gross Cross-Section Area
• Section modulus:
  $${\mathrm{S}}_{\mathrm{x}} = \frac{\mathrm{b} · {\mathrm{d}}^2}{6} = \frac{(3.50 \mathrm{in}) · {(7.24 \mathrm{in})}^2}{6} = 30.58 {\mathrm{in}}^3$$

  Section Modulus
• Moment of inertia:
  $${\mathrm{I}}_{\mathrm{x}} = \frac{\mathrm{b} · {\mathrm{d}}^3}{12} = \frac{(3.50 \mathrm{in}) · {(7.24 \mathrm{in})}^3}{12} = 110.69 {\mathrm{in}}^4$$

  Moment of Inertia

The material that will be used for this example is DF-L SS. The material properties are as follows.

• Reference bending design value: f_b = 2,393.12 psi
• Modulus of elasticity: E = 1,812,970 psi

Beam Modification Factors

For the design of timber members as per the CSA O86-14 standard, modification factors must be applied to the reference bending design value (f_b). This will ultimately provide the adjusted bending design value (F_b), as well as the factored bending moment resistance (M_r).

Below, each modification factor is further explained and determined for this example.

K_D

The load duration factor accounts for different load periods. Snow, wind, and earthquake loads are considered with K_D. This means K_D is dependent on the load case. In this case, K_D is set to 0.65 as per Table 5.3.2.2 [1], assuming a long-term load duration.

K_S

The wet service factor considers dry or wet service conditions on sawn lumber as well as cross-section dimensions. For this example, we are assuming bending at the extreme fiber and wet service conditions. Based on Table 6.4.2 [1], K_s is equal to 0.84.

K_T

The treatment adjustment factor considers wood that has been treated with fire-retardant or other strength-reducing chemicals. This factor is determined from strength and stiffness capacities based on documented time, temperature, and moisture tests. For this factor, Sec. 6.4.3 [1] is referenced. For this example, 0.95 is multiplied by the modulus of elasticity and 0.85 for all other properties when assuming wet service conditions.

K_Z

The size factor considers varying sizes of lumber and how the loading is applied to the beam. More info on this factor can be found in Sec. 6.4.5 [1]. For this example, K_Z is equal to 1.30 based on dimensions, bending and shear, and Table 6.4.5 [1].

K_H

The system factor takes into account sawn lumber members that consists of three or more essentially parallel members. These members cannot be spaced more than 610 mm apart and mutually support the load. This criteria is defined as case 1 in Sec. 6.4.4 [1]. For this example, K_H is equal to 1.10 using Table 6.4.4, because we assume it as a bending member and case 1.

K_L

The lateral stability factor considers lateral supports provided along the member length which help prevent lateral displacement and rotation. The lateral stability factor (K_L) is calculated below.

Factored Specified Strength in Bending (F_B)

The factored specified strength in bending (F_b) is determined in the section below. F_b is calculated by multiplying the specified strength for bending (f_b) by the following modification factors.

• K_D = 0.65
• K_H = 1.10
• K_s = 0.84
• K_T = 0.85

We can now calculate F_b by using the following equation from Sec. 6.5.4.1 [1].

Lateral Stability Factor, K_L

The lateral stability factor (K_L) is calculated from Sec. 6.5.4.2 [1]. Before K_L can be determined, the slenderness ratio must be calculated. First, the effective length (L_e) is found in Table 7.5.6.4.3 [1]. For this beam example, a concentrated load is applied at its center with no intermediate supports. The unsupported length (l_u) is taken as 10 ft.

• L_e = 1.61 (l_u)
• L_e = 16.10 ft

Then, the slenderness ratio (C_B) can be calculated based on Sec. 7.5.6.4.3 [1].

Since the slenderness ratio is greater than 10, C_k should be calculated. Referencing Sec. 6.4.2, K_SE is equal to 0.94.

C_B is less than C_k, so we can now calculate K_L based on Sec. 7.5.6.4 (b) [1].

Beam Design Ratio

The ultimate goal of this example is to obtain the design ratio for this simple beam. This will determine if the member size is adequate under the given load, or if it should be further optimized. Calculating the design ratio requires the factored bending moment resistance (M_r) and factored bending Moment (M_f).

The maximum moment about the x-axis (M_f) is found by the following:

Next, the factored bending moment resistance (M_r) can be calculated from Sec. 6.5.4.1 [1].
M_r = 0.90 ⋅ F_b ⋅ S ⋅ K_z ⋅ K_L
M_r = 3.63 kip ⋅ ft

Finally, the design ratio (η) can now be calculated.

Application in RFEM

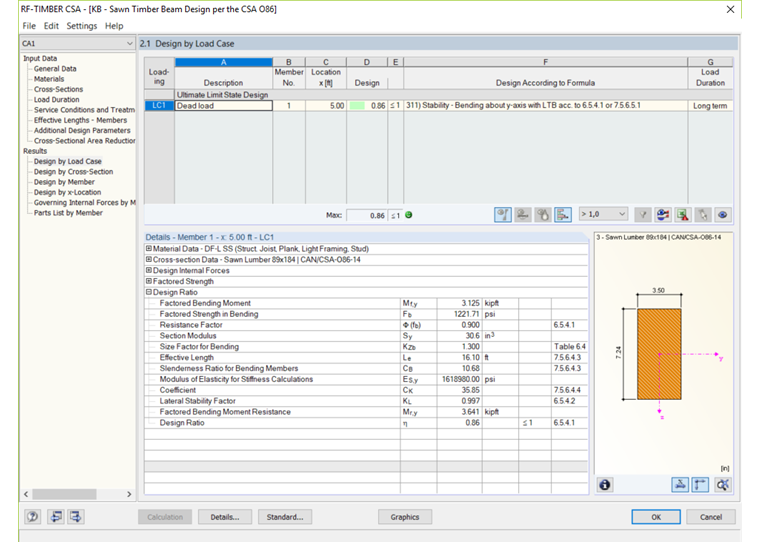
For timber design as per the CSA O86-14 standard in RFEM, the add-on module RF-TIMBER CSA analyzes and optimizes cross-sections based on loading criteria and member capacity for a single member or set of members. When modeling and designing the beam example above in RF-TIMBER CSA, the results can be compared.

2 RFEM Model

In the General Data table of the RF-TIMBER AWC add-on module, the member, loading conditions, and design methods are selected. The material and cross-sections are defined from RFEM and the load duration is set to long-term. The moisture service condition is set to wet and treatment is set to preservative (incised). The effective length (L_e) is determined from Table 7.5.6.4.3 [1]. The module calculations produce a factored bending moment (M_f) of 3.125 kip ⋅ ft and a factored bending moment resistance (M_r) of 3.641 kip ⋅ ft. A design ratio (η) of 0.86 is determined from these values, aligning well with the analytical hand calculations shown above.

3 Add-on Module RF-TIMBER CSA

Knowledge Base

KB 001631 | Timber Beam Design per the 2014 CSA Standard