As estruturas de membranas são uma das tendências atuais na engenharia civil. Destacam-se pelas formas expressivas, leveza ou utilização eficiente do material. Devido à falta de rigidez à flexão, estas estruturas têm uma forma inseparável do estado de tensão.
Isto leva à necessidade de procurar formas, que não podem ser escolhidas arbitrária. Estas estruturas com diferentes formas e formas são feitas de rolos de tecido ou folha. Os padrões de corte são formados a partir de tiras de material planas, que são unidas e esticadas na posição final para atingir a estrutura pretendida. A determinação dos padrões de corte é uma etapa sensível no processo de planeamento e a sua qualidade influencia fortemente a qualidade de toda a estrutura.
Este artigo lida em detalhe os dois processos principais - a determinação da forma de estruturas de membrana e a determinação dos padrões de corte. É dada especial atenção a conhecimentos práticos e úteis para o planeamento.
Dimensionamento de estruturas de membranas
Neste capítulo, os princípios físicos da determinação da forma para estruturas de membranas são descritos primeiro. Além disso, é discutida a viabilidade do pré-esforço necessário ao engenheiro civil. O texto é complementado por exemplos práticos para ilustrar as considerações e as teorias.
O planeamento de estruturas de membranas difere significativamente da prática habitual. Uma vez que os materiais utilizados praticamente têm apenas resistência à tração, a forma não pode ser selecionada livremente. Não é possível separar a forma do pré-esforço. Neste caso, os aspetos estéticos e físicos dos edifícios estão basicamente ligados.
A forma da estrutura de membrana é determinada pelas condições de fronteira e pelo sistema de equilíbrio espacial. O processo de form-finding pode ser descrito pela Equação (1) abaixo. A forma de equilíbrio é encontrada se o trabalho virtual não se alterar (δW = 0), isto é, se a soma do trabalho virtual responsável pelo pré-esforço necessário σ e o trabalho virtual realizado com a carga externa p (pressão positiva, peso próprio) for igual a zero.
Na equação acima, t representa a espessura do material utilizado, δ é a alteração na deformação do material e δu é a deformação sobre a superfície da estrutura Ω.
Além de alguns problemas teóricos a serem resolvidos, existe um problema de fundo. O principal problema é que é assumido um pré-esforço predefinido. No entanto, geralmente é excluída. As estruturas de membrana têm uma curvatura dupla (ou seja, a curvatura gaussiana não é igual a zero), razão pela qual exclui um pré-esforço ortotrópico homogéneo. Em teoria, é quase impossível um estado onde existe um valor de pré-esforço específico na direção da urdidura e um valor de pré-esforço preciso na direção da trama em cada ponto da membrana. A única exceção é o pré-esforço isotrópico, que pode ser alcançado se a forma for fisicamente real sob as condições de fronteira dadas.
Assim, o próprio pré-esforço deve ser encontrado. O objetivo do processo (form-finding) não é apenas encontrar uma forma desconhecida para um pré-esforço dado, mas também procurar uma forma desconhecida para um pré-esforço geralmente desconhecido. Este pré-esforço é aproximado por um valor especificado pelo engenheiro civil para as direções da urdidura e da trama. Foram desenvolvidos vários métodos para a determinação da forma. Se utilizar diferentes programas para a resolução de problemas, pode obter resultados mais ou menos diferentes para os mesmos dados de entrada. Depois, surge a questão sobre qual das soluções é a ideal. A seguir, são apresentados alguns exemplos de diferentes estruturas e pré-esforços necessários.
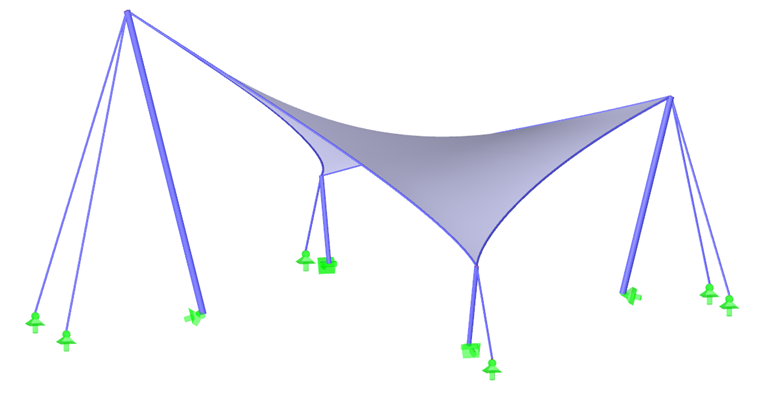
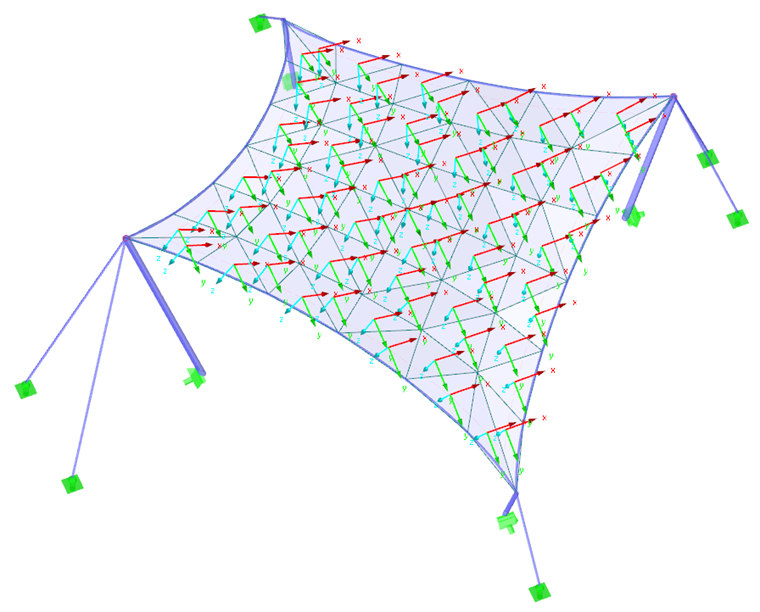
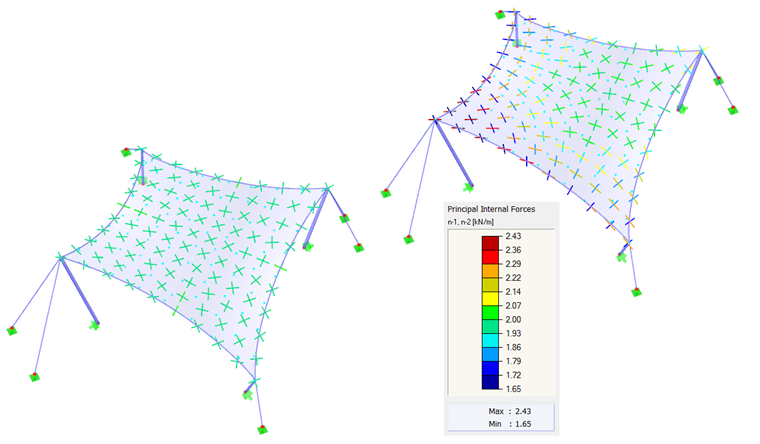
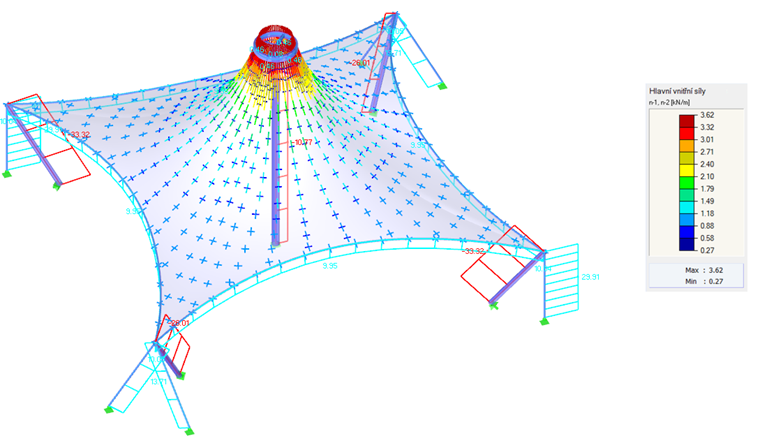
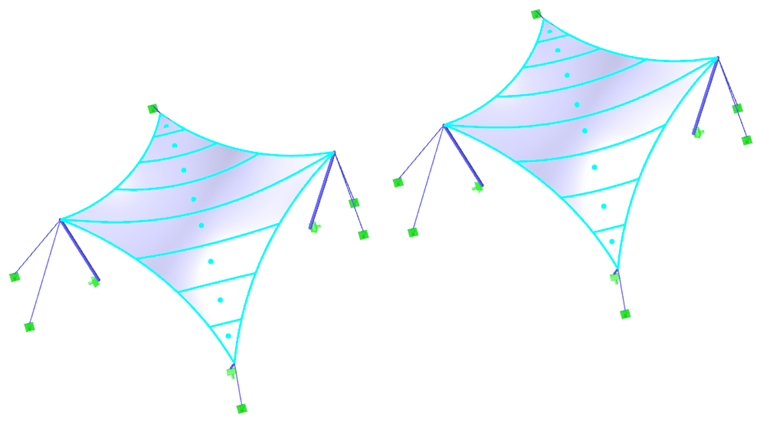
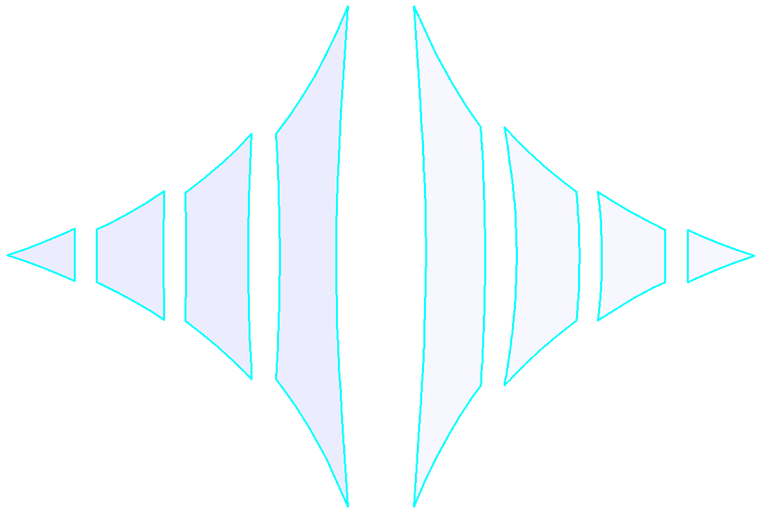
Como primeiro exemplo, iremos utilizar um paraboloide hiperbólico (Figura 2 e Figura 3). São aplicados pré-esforços isotrópicos e orotrópicos. Para o pré-esforço isotrópico, resultam dois resultados diferentes do processo de form-finding (Figura 4 e Figura 5), os quais também são brevemente descritos. Os valores introduzidos para o pré-esforço isotrópico são nurdidura = ntrama = 2,00 kN/m. Os cabos de perímetro têm uma flecha relativa de s = 8,00%. Os resultados são exibidos como vectores das forças internas principais e uma escala de cores.
Se são obtidos dois resultados diferentes para os mesmos dados de entrada, surge naturalmente a questão qual é a solução correta. Em teoria, as duas soluções estão corretas porque atingiram um estado de equilíbrio e também são viáveis. No entanto, a solução apresentada à esquerda mostra um pré-esforço uniforme que não está concentrado nas áreas de canto. Tais efeitos locais são considerados indesejados porque reduzem a capacidade de carga da estrutura e resultam em efeitos reológicos irregulares. Portanto, a solução apresentada à esquerda é vantajosa. Geralmente, é considerado favorável encontrar uma forma com um pré-esforço uniformemente distribuído e não concentrado localmente. A estrutura de membrana é assim bem pré-esforçada e a sua capacidade de carga não é reduzida em algumas áreas por pré-esforço excessivo.
Conforme já mencionado, um pré-esforço isotrópico é o único pré-esforço homogéneo que pode ser gerado com precisão. A precisão realizável é limitada na prática apenas pelo tamanho da malha de EF. No caso de uma malha definida de forma aproximada, não é possível aproximar exatamente um estado de equilíbrio e, como tal, os valores podem divergir dos pré-esforços introduzidos. No entanto, tais desvios devem ser pequenos e também uma malha mais grossa não leva necessariamente a um pré-esforço claramente mais concentrado.
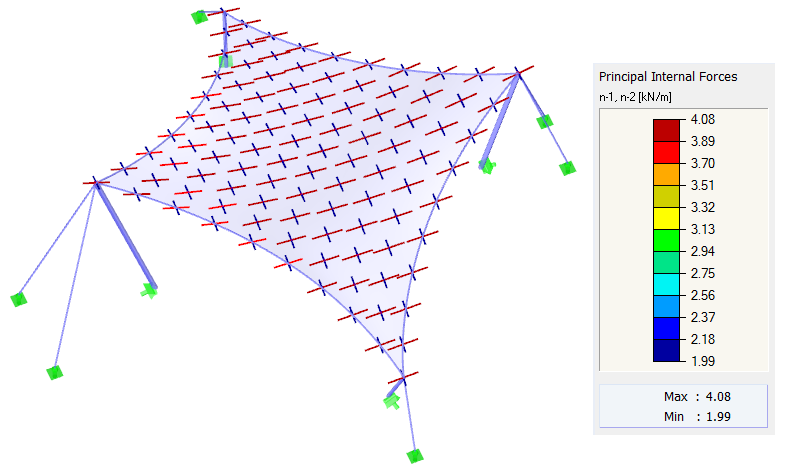
Para o outro cálculo são aplicadas as mesmas condições de fronteira. O pré-esforço é definido como ortotrópico com valores n deurdidura = 4,00 kN/m etrama = 2,00 kN/m. Os cabos de perímetro têm uma flecha relativa de s = 8,00%. Como mencionado acima, um pré-esforço ortotrópico homogéneo exato não pode ser alcançado porque isso não é teoricamente possível com a curvatura dupla das estruturas de membrana. No entanto, é possível obter uma forma com um pré-esforço que se aproxima dos valores especificados (Figura 5). O resultado é um pré-esforço uniformemente distribuído que se aproxima dos valores introduzidos. Com esta estrutura, não existe qualquer razão para concentrações significativas.
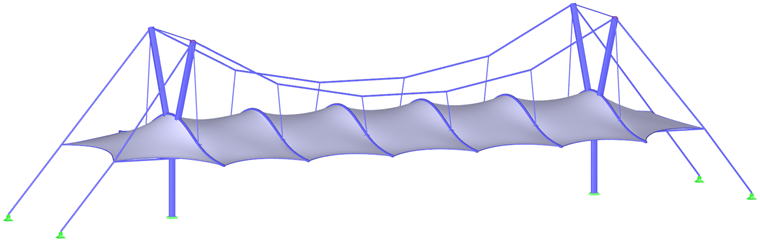
Para a maioria das formas, incluindo paraboloides hiperbólicos, membranas suportadas por arcos ou pneumáticas (Figura 1), o pré-esforço resultante pode ser distribuído uniformemente sem a necessidade de concentrações locais de pré-esforço. Para formas cónicas altas não é possível evitar áreas com pré-esforço concentrado. Quaisquer concentrações ocorrem no vértice do cone, mas não são necessárias nem desejadas nos cantos inferiores (Figura 6).
Se é necessário ou não um pré-esforço concentrado, pode ser deduzido intuitivamente a partir da seguinte fórmula (2). A equação representa um equilíbrio de forças num ponto onde n1 e n2 são as forças internas principais, 1/R1 e 1/R2 são as curvaturas na direção destas forças internas principais e p qualquer carga externa.
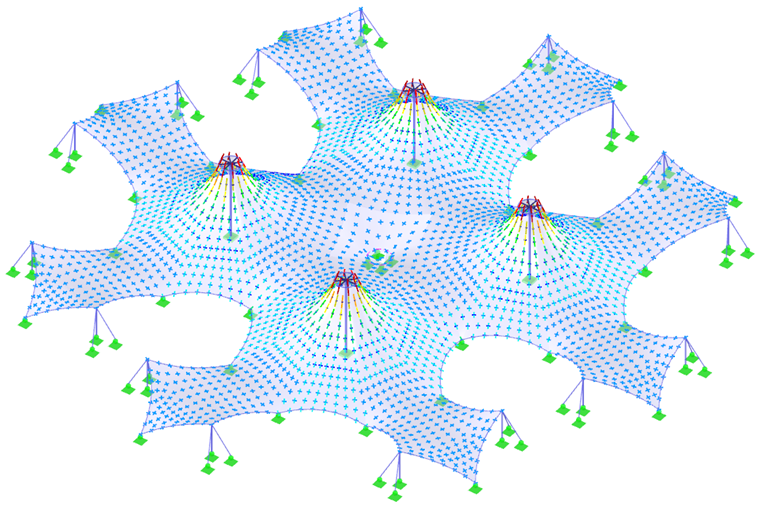
No caso de uma estrutura anticlástica, cujo peso próprio quase não influencia a forma encontrada, o equilíbrio de forças num nó é dado pelo pré-esforço e pelas curvaturas na direção oposta. A questão agora é se a curvatura da estrutura tem de se alterar tão rapidamente. Se assim for, o pré-esforço concentrado localmente é próprio da estrutura; caso contrário, a concentração de pré-esforço não é necessária para a estrutura. Este método pode ser aplicado aos nossos exemplos. As formas sem áreas cónicas (Figura 4, Figura 5, Figura 8 e Figura 10, exceto para as áreas cónicas) não requerem alterações rápidas da curvatura, razão pela qual podem ser pré-esforçadas uniformemente. As áreas cónicas apresentam alterações rápidas das curvaturas radial e tangencial e, portanto, não é possível evitar uma alteração rápida do pré-esforço (Figura 6 e áreas cónicas na Figura 10).
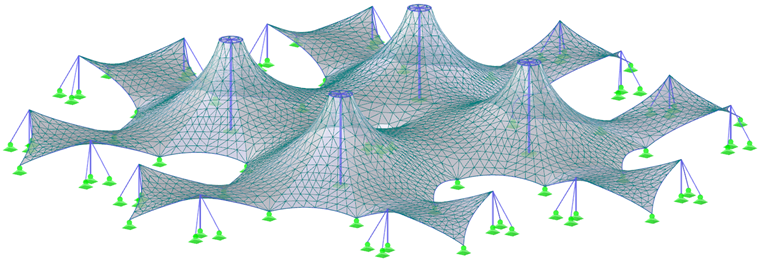
Duas estruturas mais complexas (Figura 7 e Figura 9) e os seus pré-esforços (Figura 8 e Figura 10) são apresentados no final deste capítulo. Para alcançar os resultados mais precisos possíveis no processo de form-finding, bem como na análise estrutural, a estrutura deve ser modelada como um todo e não separada em partes. Assim, é considerada a interação de todas as partes da estrutura e a redistribuição das forças através das deformações.
Corte de estruturas de membrana
O processo de determinação dos padrões de corte é explicado a seguir. Descreve as etapas individuais do processo e depois apresenta um exemplo prático para mostrar como as propriedades do material podem afetar as formas dos padrões de corte.
Conforme mencionado, a curvatura dupla é uma das características típicas das estruturas de membrana, razão pela qual a sua forma não pode ser desenvolvida num plano. No entanto, as membranas são feitas de rolos de tecidos planos. Para isso, deve ser gerado um corte (isto é, padrões de corte planos individuais) que se aproxime dos padrões correspondentes no espaço. O processo de criação de um padrão de corte consiste em duas etapas. Primeiro, a estrutura da membrana é dividida em padrões de corte espaciais individuais através de linhas de corte; então, é encontrada a melhor aproximação possível dos padrões de corte planos em relação ao espacial.
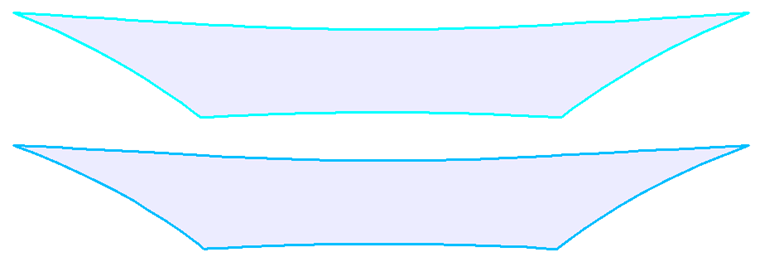
Em teoria, uma estrutura de membrana pode ser dividida em faixas parciais através de qualquer linha de corte. No entanto, por razões práticas, são geralmente utilizadas linhas de corte geodésicas (Figura 11, esquerda), as quais são preferidas por causa do eixo reto dos padrões de corte após o aplainamento (Figura 12, esquerda). As secções planas (Figura 11, direita) que não são retas após o aplainamento (Figura 12, direita) são utilizadas com menos frequência e isto resulta numa maior necessidade de material.
O segundo passo para criar um padrão de corte é muito mais complexo: encontrar a melhor aproximação possível de um padrão de corte plano para o correspondente padrão de corte espacial. Foram concebidos vários métodos para este processo; os mais antigos utilizaram um método geométrico simplificado e os mais recentes métodos de mapeamento matemático avançado. Os métodos atuais baseiam-se na mecânica contínua com uma análise não linear utilizando o método dos elementos finitos (MEF) para a determinação do padrão de corte.
O último método é considerado a solução mais geral para um problema de aproximação e permite considerar as propriedades do material do tecido ou da membrana utilizada. Se não pretende considerar as propriedades ortotrópicas do material têxtil ou a contracção transversal, pode aplicar um material isotrópico com um coeficiente de Poisson v = 0. Contudo, se as propriedades do material devem ser incluídas no processo Além do aplainamento do padrão de corte, pode ser alcançada a forma ideal do padrão de corte.
Ao testar os materiais têxteis utilizados para estruturas de membrana, geralmente o utilizador determina as rigidezes nas direções da urdidura e da trama e o coeficiente de Poisson'. A rigidez ao corte é geralmente negligenciada. O exemplo seguinte mostra como a rigidez ao corte afeta a forma do padrão de corte resultante. Para o exemplo, selecionamos um dos padrões de corte centrais do paraboloide hiperbólico (Figura 11). Foram utilizados dois materiais diferentes para o padrão de corte.
Os seguintes valores são fornecidos para o primeiro tecido com superfície tratada:
Urdidura E = 1600 kN/m
Trama E = 1200 kN/m
vUrdidura/trama = 0,05
G = 400 kN/m
O outro material, uma malha têxtil sem tratamento de superfície, tem os seguintes valores:
Urdidura E = 1600 kN/m
Trama E = 1200 kN/m
vUrdidura/trama = 0,05
G = 10 kN/m
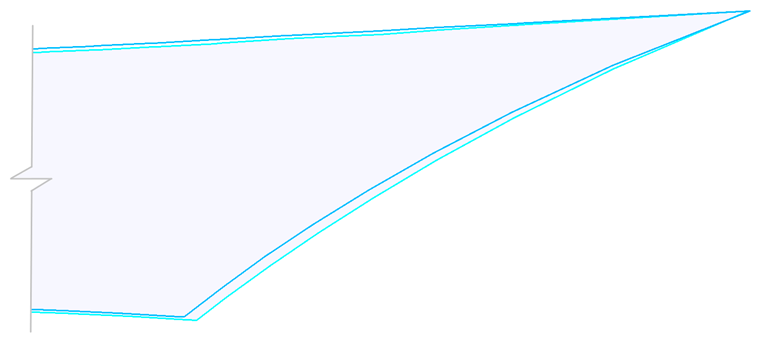
A figura seguinte mostra os padrões de corte planos resultantes. Ao mover os centros de gravidade de ambos os padrões de corte para o mesmo ponto e aumentar a parte direita dos padrões de corte no recorte (Figura 14), a diferença entre as duas formas torna-se clara. Se considerar as propriedades do material, pode obter padrões de corte de melhor qualidade. Após a montagem da estrutura, o pré-esforço real está mais próximo do pré-esforço pretendido.
Para a determinação dos padrões de corte, também é utilizada uma compensação que é determinada por ensaios biaxiais e simula a Dissolução do pré-esforço no tecido.
Um cálculo não linear de acordo com o método dos elementos finitos providencia um padrão de corte plano energético óptimo em relação ao espacial. Uma vez que se baseia em princípios físicos, este método de cálculo é o mais natural.
Além da criação de um padrão de corte, também é possível considerar outros requisitos do dimensionamento. Geralmente, é necessário manter comprimentos iguais das bordas adjacentes de padrões de corte adjacentes. Frequentemente, é necessária a aplicação de uma compensação diferente para algumas bordas dos padrões de corte. Isto é muitas vezes designado de descompensação das bordas. Em conformidade com estes requisitos de dimensionamento e utilizando uma análise não linear, é encontrado um padrão de corte otimizado energéticamente.
Conclusão
O objetivo deste artigo foi explicar os principais processos envolvidos no planeamento de estruturas de membranas. Os princípios físicos devem ser explicados e as teses individuais ilustradas com exemplos. Estes exemplos foram criados no software de engenharia RFEM da Dlubal Software GmbH [2].
Obrigado
Este artigo foi criado com o apoio do projeto FAST-J-15-2803.
Autores
Ing. Rostislav Lang
Doc. Ing. Ing. Něm Němec, CSc.
Ing. Hynek Štekbauser
Instituto de Mecânica Estrutural, BUT FCE Brno, consultoria em FEM Brno
Verificador
O Prof. Ing. Jiri Studnica, DrSc., Universidade Técnica de Praga
![Formas básicas de estruturas de membrana [1]](/pt/webimage/009595/2419507/01-png.png)