膜结构是当前土木工程领域的一种发展趋势。 它们的特点是形状生动、重量轻,或材料利用率高。 由于缺乏抗弯刚度,这些结构在受力状态下具有不可分割的形状。
因此需要寻找它们的形状,而不能任意选择。 这些结构具有不同的形状和形状由织物或薄膜卷筒制成。 裁剪式样是由平面材料条带组成,通过将它们连接并在最终位置拉伸就可以达到预期的结构。 裁剪式样的确定是结构设计过程中的一个敏感步骤,其质量直接影响到整个结构的质量。
在本文中,将详细介绍膜结构计算的两个主要过程-确定膜结构的形状和确定裁剪式样。 该课程特别关注规划方面的实用信息。
膜结构设计
本章首先介绍膜结构形状确定的物理原理。 此外,还要讨论土木工程师们要求的预应力的可行性。 书中还结合了实际案例来阐述所考虑的理论和方法。
膜结构的设计与通常的膜结构设计有很大的不同。 由于实际使用的材料只有抗拉承载力,所以形状不能自由选择。 形状不能从预应力中分离出来。 在这种情况下,建筑物的美学和物理方面基本上是相互联系的。
膜结构的形状由边界条件和空间平衡体系决定。 找形分析过程可以用下面的公式 (1) 来描述。 如果虚功 (δW = 0) 不变,即产生所需预应力 σ 的虚功与施加外部荷载 p(正压,自重)的虚功之和,则找到平衡形状为零。
公式中 t 为材料的厚度,δent 为材料位移的变化值,δu 为结构截面的位移 ω。
为此除了解决一些理论问题外,还需要解决一个根本性的问题。 主要问题是假定预设的预应力。 但是一般不包含这种情况。 膜结构为双曲率(即高斯曲率不为零),因此不适用均匀正交各向异性预应力。 理论上,膜结构上每一点经向有特定的预应力,纬向有一个精确的预应力值。 唯一的例外是各向同性预应力,如果在给定的边界条件下,其形状是真实的。
因此,必须找出预应力。 找形过程的目的不仅是找到给定预应力的未知形状,而且是寻找通常未知的预应力的未知形状。 并由工程师在经向和纬向近似给出预应力。 已经发展了多种找形方法。 例如,对于相同的输入数据,使用不同的软件进行求解可能会得出不同的结果。 那么问题来了,哪种方案是最优的。 下文将举例说明一些不同的结构形式和所需的预应力。
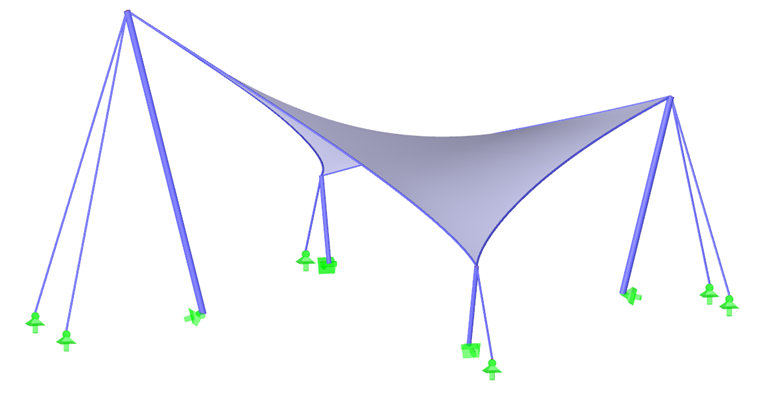
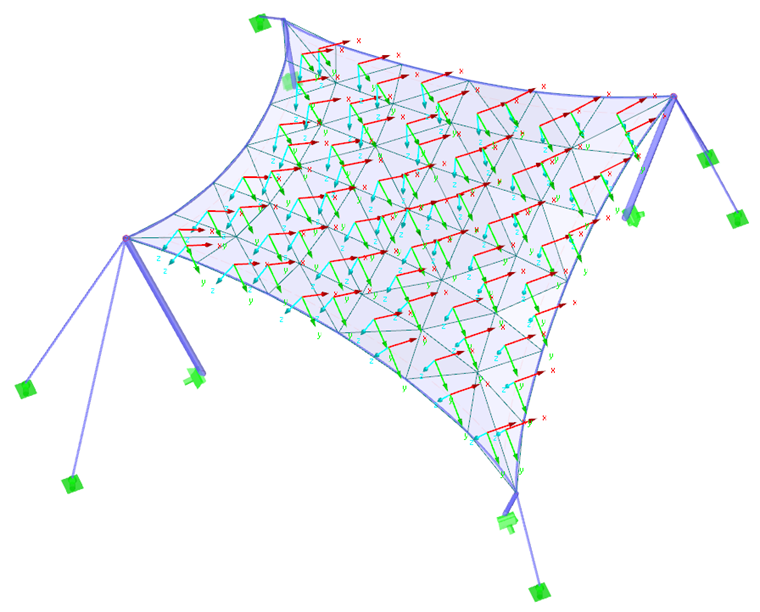
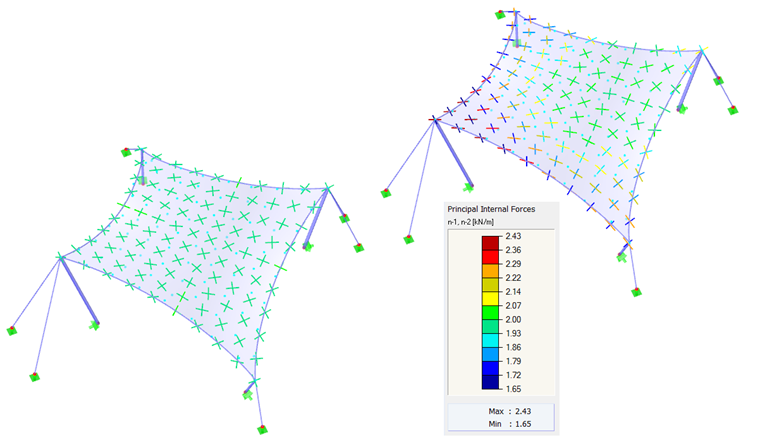
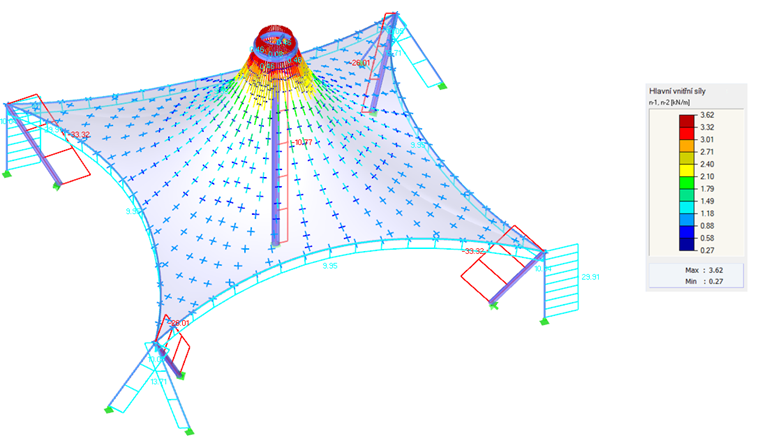
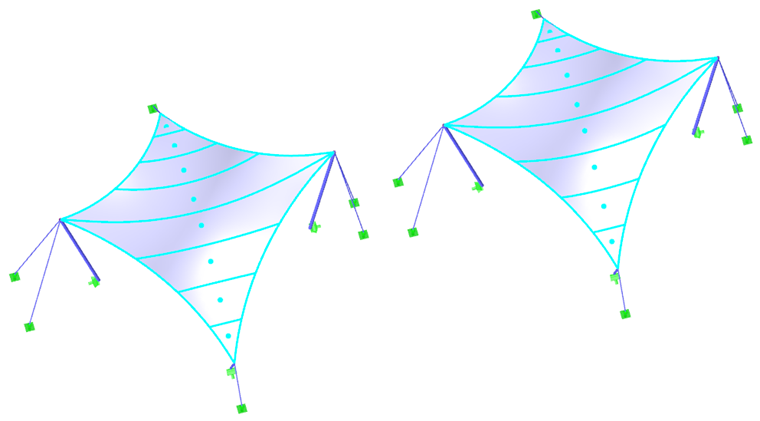
第一个例子是双曲抛物面(图 2和图 3)。 应用各向同性和各向异性预应力。 对于各向同性预应力,找形过程中会得出两个不同的结果(图 4 和图 5),下面在这里做简单的说明。 输入各向同性预应力的数值为 n经向= n纬向= 2.00 kN/m。周边索的相对垂度 s = 8.00 %。计算结果显示为主内力向量和色阶。
如果对相同的输入数据获得两个不同的结果,那么自然就会出现一个问题,哪个解决方案是正确的。 从理论上讲,这两种解都是正确的,因为它们都已达到平衡状态,并且也是可行的。 左图显示的是均匀的预应力,它并不集中在拐角处。 这种局部作用是不希望出现的,因为它们会降低结构的承载力,并产生不均匀的流变效应。 因此,左侧所示的解决方案是有利的。 一般来说,预应力均匀且不局部集中的形状被认为是有利的。 该膜结构得到了良好的预应力,并且其承载能力没有由于预应力过大而在某些区域没有降低。
如前所述,各向同性预应力是唯一可以精确实现的均匀预应力。 有限元网格的尺寸会限制精度。 网格划分粗略不能精确地近似于平衡状态,因此数值可能与输入的预应力有偏差。 然而,这种偏差应该在一个很小的范围内,并且网格越粗糙并不一定意味着预应力明显越集中。
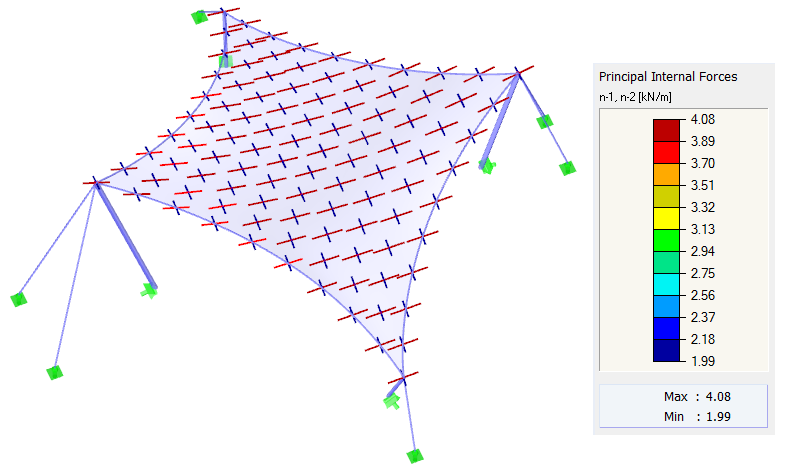
同样的边界条件也适用于其他计算。 预应力定义为正交各向异性的,n值为经= 4.00 kN/m,纬= 2.00 kN/m。周边索的相对垂度 s = 8.00 %。如上所述,对于双曲膜结构,理论上不能实现精确均匀的正交各向异性预应力。但是,也可以得到一个非常接近于给定值的预应力的形状(图5)。计算后得到的预应力接近输入值的均匀分布的预应力。这种结构不会出现明显的集中现象。
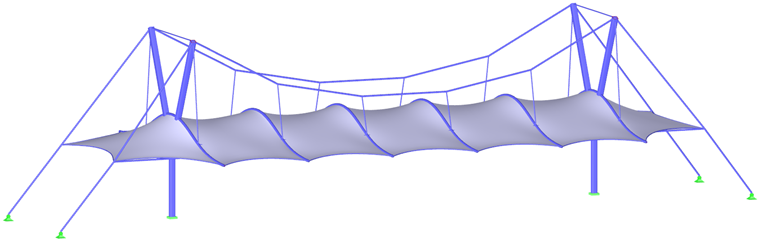
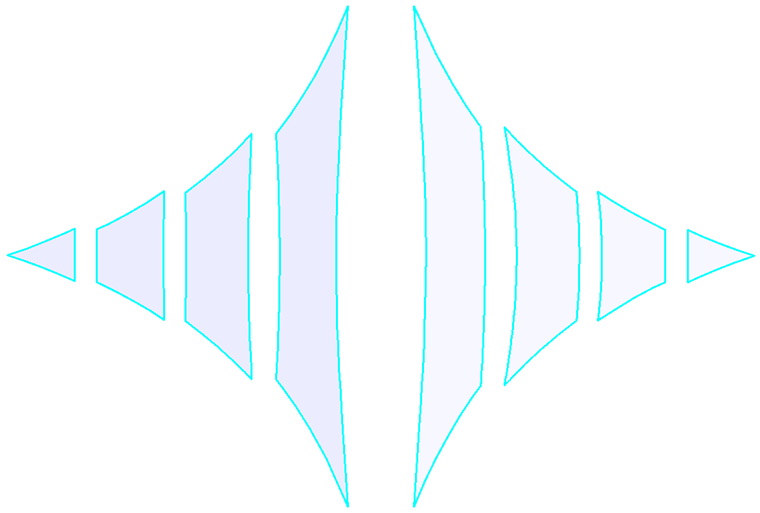
对于大多数形状,例如双曲抛物面膜、弧形支撑膜或充气膜(图1),不需要设置局部集中预应力,就可以得到均匀分布的预应力。 对于高的圆锥形,要避免出现集中预应力区域是不可能的。 在锥体的顶点会出现集中应力,但在下部的拐角处则不需要(图6)。
是否需要设置集中预应力可以从下面的公式(2)中直观地得出。 公式表示杆件在某一点处的平衡状态,其中 n1 和 n2 为主内力,1/R1 和 1/R2 为主内力作用方向上的曲率,p 为外荷载。
对于反塑性结构,其自重对已建立的形状几乎没有影响,节点处力的平衡由预应力和相反方向的曲率给出。 现在的问题是,结构的曲率是否必须如此迅速地变化。 如果是,说明局部集中预应力是结构固有的。否则,对于结构来说就不需要定义预应力集中。 这种方法可以应用于我们的示例中。 不带锥形区域的形状(图4、图5、图8和图10,锥形区域除外)不需要曲率快速变化,因此可以施加均匀预应力。 锥形区域的径向和切向曲率变化很快,因此预应力的快速变化是不可避免的(图 6 和图 10 中的锥形区域)。
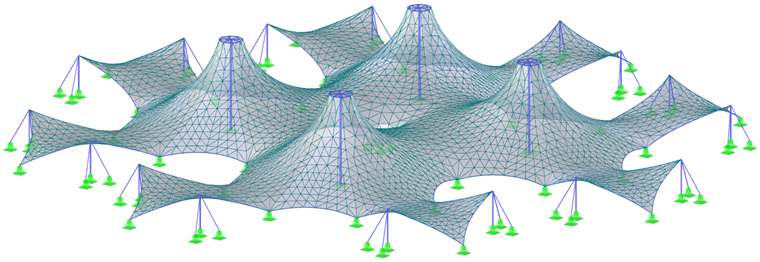
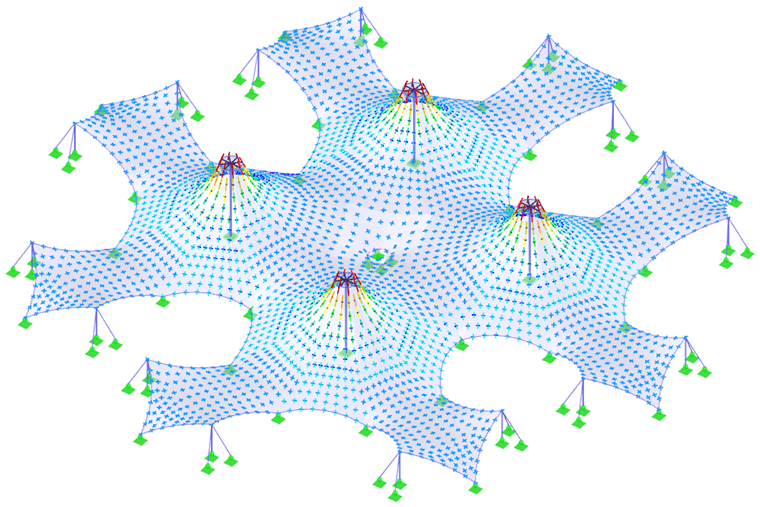
在本章的末尾列出了两个更复杂的结构(图7和图9)及其预应力(图8和图10)。 为了在找形分析和结构分析过程中获得最准确的结果,建议结构作为一个整体进行建模,而不是分成多个部分。 同时考虑了结构各部分之间的相互作用以及变形引起的内力分布。
裁剪膜结构
下面将介绍如何确定裁剪式样。 首先介绍了裁剪过程的各个步骤,然后通过实例说明材料属性是如何影响裁剪式样的。
如前所述,双曲率是膜结构的典型特征之一,这就是为什么它的形状不能在一个平面上发展的原因。 然而,膜由平面织物卷筒制成。 为此,必须生成在空间中近似于其相应图案的裁剪(即,单个平面裁剪式样)。 创建裁剪式样包含两个步骤。首先,通过裁剪线将膜结构划分为空间裁剪图形;然后,找到平面裁剪式样最接近空间裁剪式样的方法。
理论上,膜结构被任意的裁剪线分割成条带。 但出于实际原因,通常使用大地裁剪线(图 11 左),因为展平后裁剪式样的轴线是直的(图 12 左)。 在展平(图 12 右侧)之后不再是直线的平面截面(图 11 右侧)很少使用,因此对材料的要求也更高。
创建裁剪式样的第二步要复杂得多:为平面裁剪式样找到相应的空间裁剪式样的最佳近似。 为此设计了多种方法;历史上最古老的方法使用的是简化的几何方法,后期的方法则使用高级的数学映射。 目前的方法是基于连续介质力学,通过使用有限元法(FEM)的非线性分析来确定裁剪式样。
后一种方法是近似问题的最一般的解决方案,并且可以考虑所用薄膜或薄膜的材料属性。 如果不想考虑纺织材料的正交各向异性或横向收缩,则可以使用各向同性材料,泊松比 v = 0。但是,如果要考虑材料属性通过展平裁剪式样,可以得到最佳的裁剪式样形状。
对于用于膜结构的纺织材料,通常需要测定经向和纬向的刚度以及泊松比。 抗剪刚度通常被忽略。 下面的例子显示了剪切刚度如何影响裁剪式样的形状。 在本示例中,我们选择了双曲线抛物面的中间裁剪式样(图 11)。 该裁剪式样使用了两种不同的材料。
下列数值是针对第一种表面处理的织物:
Ewarp = 1600 kN/m
E纬= 1200 kN/m
v经向/纬向= 0.05
G = 400kN/m
另一种材料,即未经表面处理的纺织网格,具有以下属性值:
Ewarp = 1600 kN/m
E纬= 1200 kN/m
v经向/纬向= 0.05
G = 10kN/m
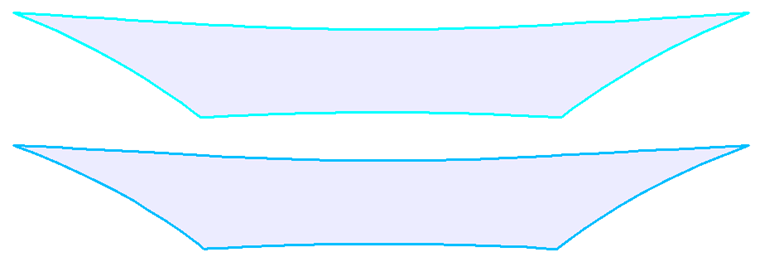
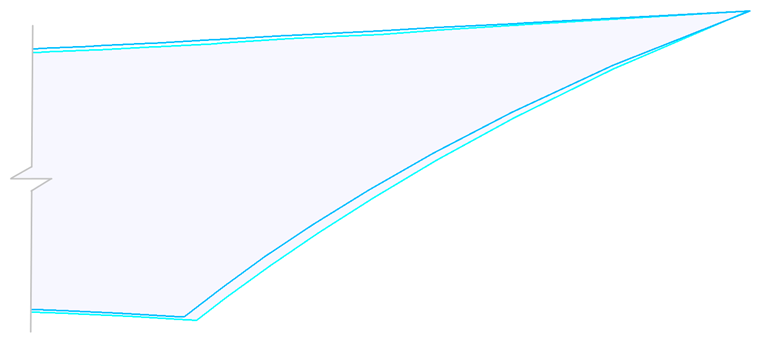
下图显示了生成的平面裁剪式样。 通过将两种裁剪式样的重心移到同一点上,并在裁剪中放大裁剪式样的右侧部分(图 14),可以清楚地看到两种裁剪式样之间的差异。 如果考虑材料属性,可以获得更好的裁剪式样。 结构装配后,实际预应力更接近设计预应力。
在确定裁剪式样时,使用了一种补偿,该补偿通过双向试验来确定,模拟预应力在织物中的消失。
根据有限元法的非线性计算提供了一种与空间裁剪式样在能量上最佳的平面裁剪式样。 既然是基于物理学的原理,那么这种计算方法是最自然的。
在创建裁剪式样时,还可以考虑其他的设计要求。 主要原因是相邻裁剪式样的相邻边的长度必须保持相等。 通常,需要对裁剪式样的某些边缘应用不同的补偿。这通常称为边缘失补偿。 在满足这些设计要求的情况下,使用非线性分析找到了一种在能量上进行优化的裁剪式样。
概述总结
本文的目的是介绍膜结构设计中的主要步骤。 每一门课程都应该讲解物理原理,并举例说明。 这些示例是在 Dlubal Software GmbH [2] 工程软件 RFEM 中创建的。
致谢
本文是在 FAST-J-15-2803 项目的支持下创建的。
作者
Ing.罗季斯拉夫朗
文件 Ing. Ing. Něm Němec, CSc.
Ing. Hynek štekbauser
BUT FCE Brno, FEM consulting Brno
校核
Prof. Ing. Jiri Studnica,博士,捷克技术大学布拉格分校
![膜结构的基本形状[1]](/zh/webimage/009595/2419509/01-png.png)