Мембранные конструкции являются одним из современных направлений гражданского строительства. которые выделяются благодаря выразительным формам, легкости или эффективному использованию материала. Из-за отсутствия жесткости на изгиб, эти конструкции имеют форму, не отделимую от напряженного состояния.
Это приводит к необходимости поиска их формы, которая не может быть выбрана произвольно. Эти конструкции различной формы и формы сделаны из рулонов ткани или плёнки. Раскройные формы формируются из плоских полос материала, которые соединяются и растягиваются в конечном положении, а затем вы достигаете предполагаемой конструкции. Определение раскройных форм - это ответственный шаг в процессе планирования, который сильно влияет на качество всей конструкции.
В данной статье подробно рассматриваются два основных процесса - формообразование мембранных конструкций и определение раскройных форм. Особое внимание уделяется практической и полезной информации для планирования.
Расчёт мембранных конструкций
В этой главе в первую очередь будут описаны физические принципы определения формы мембранных конструкций. Обсуждается также возможность предварительного напряжения по требованиям инженера-строителя. Затем текст дополняется практическими примерами, поясняющими все рассуждения и теории.
Проектирование мембранных конструкций существенно отличается от обычной практики. Поскольку используемые материалы практически обладают только сопротивлением растяжению, форма не может быть выбрана свободно. Невозможно отделить форму от предварительного напряжения. В данном случае эстетические и физические аспекты здания в основном связаны.
Форма мембранной конструкции определяется граничными условиями и системой пространственного равновесия. Процесс поиска формы можно описать с помощью уравнения (1). Форма равновесия найдена, если виртуальная работа не изменяется (δW = 0), то есть сумма виртуальной работы, выполняющей требуемое предварительное напряжение σ, и виртуальной работы, выполняющей внешнюю нагрузку p (избыточное давление, собственный вес) равна равна нулю.
В приведённом выше уравнении t представляет собой толщину используемого материала, δê - изменение деформации материала, а δu - деформацию по поверхности конструкции Ω.
Кроме некоторых теоретических проблем, которые необходимо решить, существует фундаментальная проблема. Основная проблема заключается в том, что в данном случае предполагается заданное предварительное напряжение. Однако, как правило, это исключается. Мембранные конструкции имеют двойную кривизну (то есть гауссову кривизну не равна нулю), поэтому они исключают однородное ортотропное предварительное напряжение. Теоретически состояние, при котором в каждой точке мембраны существует конкретное значение предварительного напряжения в направлении основы и точное значение предварительного напряжения в направлении утка, практически невозможно. Единственным исключением является изотропное преднапряжение, которое достигается, если форма физически реальна при заданных граничных условиях.
Таким образом, необходимо найти также само предварительное напряжение. Целью процесса (поиск формы) является не только поиск неизвестной формы для заданного предварительного напряжения, но и поиск неизвестной формы для вообще неизвестного предварительного напряжения. Данное предварительное напряжение аппроксимируется значением, указанным инженером-строителем для направлений депланации и утка. Для поиска формы был разработан ряд методов. Однако, если использовать для решения разных задач разные программы, то при одинаковых входных данных можно получить более или менее различные результаты. Тогда, конечно, возникает вопрос, какое решение является оптимальным. Некоторые примеры различных конструкций и требуемых предварительных напряжений приведены в следующем тексте.
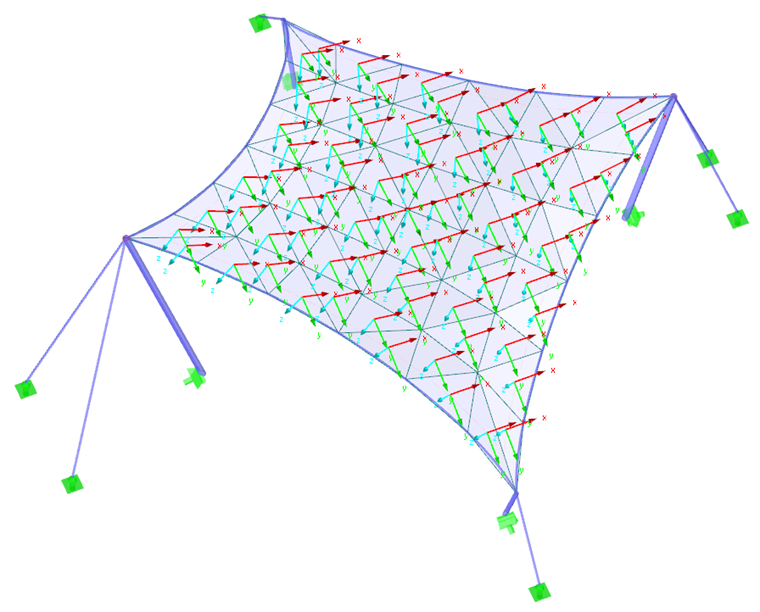
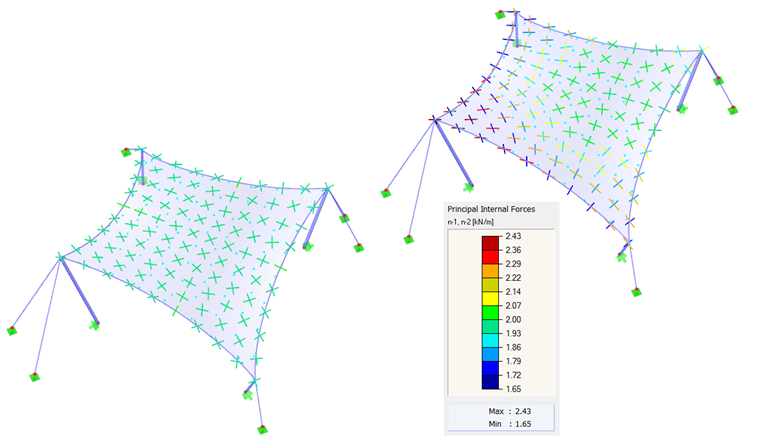
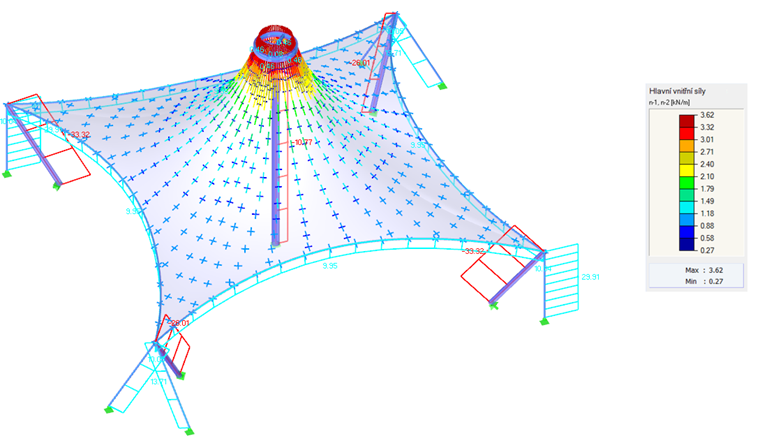
В качестве первого примера возьмем гиперболический параболоид (рисунок 2 и рисунок 3). Применяется как изотропное, так и ортотропное предварительное напряжение. Для изотропного предварительного напряжения в процессе поиска формы мы получим два различных результата (рисунки 4 и 5), которые мы также кратко прокомментируем. Для изотропного предварительного напряжения были заданы следующие значения nдепланация = nуток = 2,00 кН/м. Ванты контура имеют относительный провес s = 8,00%. Результаты изображаются в виде векторов главных внутренних сил и в цветовой шкале.
Если для одних и тех же входных данных получены два различных результата, то естественно возникает вопрос, которое из них является правильным. Теоретически оба решения правильны, потому что оба достигли состояния равновесия и оба выполнимы. Однако, решение, показанное слева, показывает равномерное предварительное напряжение, которое не сосредоточено в угловых областях. Такие локальные воздействия считаются нежелательными, поскольку они уменьшают несущую способность конструкции и приводят к неравномерным реологическим эффектам. Поэтому решение, показанное слева, является более подходящим. Как правило, считается благоприятным найти форму с равномерно распределенным и не локально сосредоточенным предварительным напряжением. Таким образом, мембранная конструкция хорошо преднапряжена, и ее несущая способность не уменьшается в некоторых областях из-за чрезмерного предварительного напряжения.
Как уже упоминалось, изотропное предварительное напряжение - это единственное однородное предварительное напряжение, которое может быть достигнуто точно. Достигаемая точность практически ограничена только размером сетки КЭ. Потому, в случае грубой сетки, состояние равновесия не может быть точно аппроксимировано, и, таким образом, значения могут отклоняться от заданных предварительных напряжений. Тем не менее, такие отклонения должны быть в небольшом диапазоне, а также более грубая сетка не обязательно приведет к более сосредоточенному предварительному напряжению.
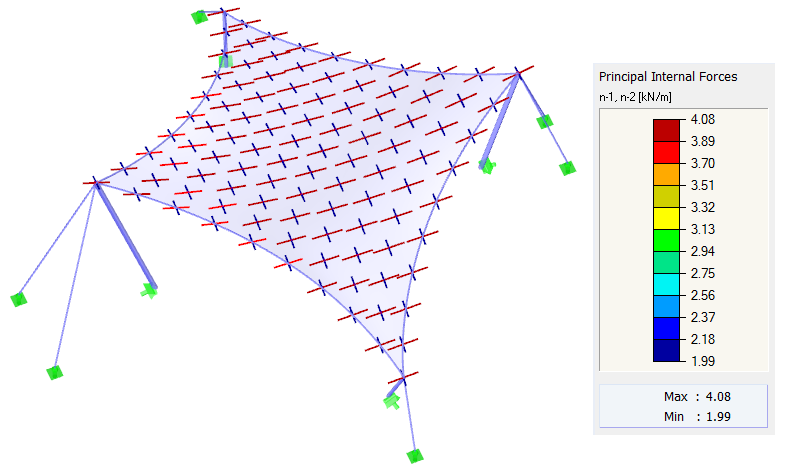
Для другого расчета применяются те же граничные условия. Предварительное напряжение зададим как ортотропное со значениями n пооснове = 4,00 кН/м иутоку = 2,00 кН/м. Ванты контура имеют относительный провес s = 8,00%. Как упоминалось выше, точное однородное ортотропное предварительное напряжение не может быть достигнуто, потому что это теоретически возможно для двойной кривизны мембранных конструкций. Тем не менее, можно получить форму с предварительным напряжением, которое близко к заданным значениям (рисунок 5). Результатом является равномерно распределенное предварительное напряжение, соответствующее заданным значениям. При данной конструкции нет оснований для каких-либо значительных концентраций.
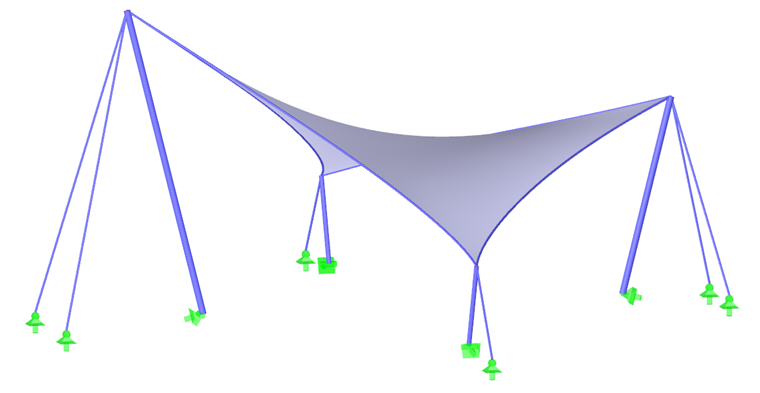
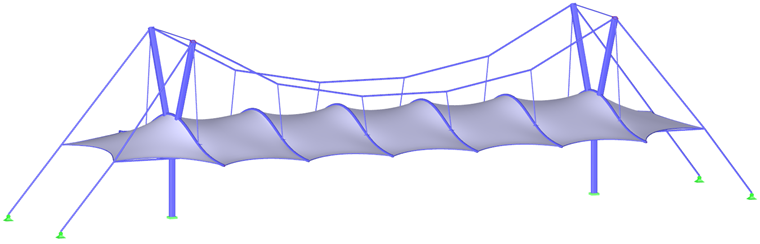
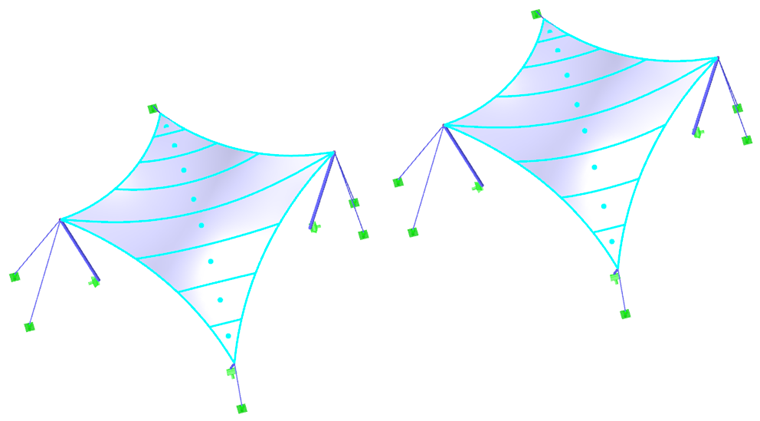
Для большинства форм, включая гиперболические параболоиды, мембраны с дуговой опорой или пневматические мембраны (рисунок 1), результирующее предварительное напряжение может быть равномерно распределено без необходимости местных концентраций предварительного напряжения. Однако у высоких конических форм невозможно избежать зон с сосредоточенным предварительным напряжением. На вершине конуса возникают любые концентрации, но в нижних углах они ни необходимы, ни желательны (рисунок 6).
Необходимость сосредоточенного предварительного напряжения можно легко определить интуитивно по формуле (2). Уравнение представляет собой равновесие сил в точке, где n1 и n2 - главные внутренние силы, 1/R1 и 1/R2 - кривизна в направлении этих главных внутренних сил, а p - любая внешняя нагрузка.
В случае антикластической конструкции, собственный вес которой практически не влияет на найденную форму, равновесие сил в узле задается предварительным напряжением и кривизной в противоположном направлении. Возникает вопрос, должна ли кривизна конструкции изменяться так быстро. Если да, то локально сосредоточенное предварительное напряжение присуще конструкции; в противном случае, для конструкции вообще не будет необходимости. Данный метод можно применить и в наших примерах. Формы без конических областей (Рисунок 4, Рисунок 5, Рисунок 8 и Рисунок 10, за исключением конических областей) не требуют быстрых изменений кривизны, поэтому они могут быть предварительно напряжены равномерно. В конических областях показаны быстрые изменения радиальной и тангенциальной кривизны, поэтому нельзя избежать быстрого изменения предварительного напряжения (рисунок 6 и конические области на рисунке 10).
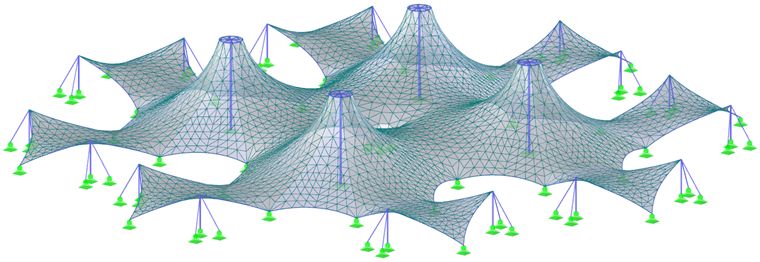
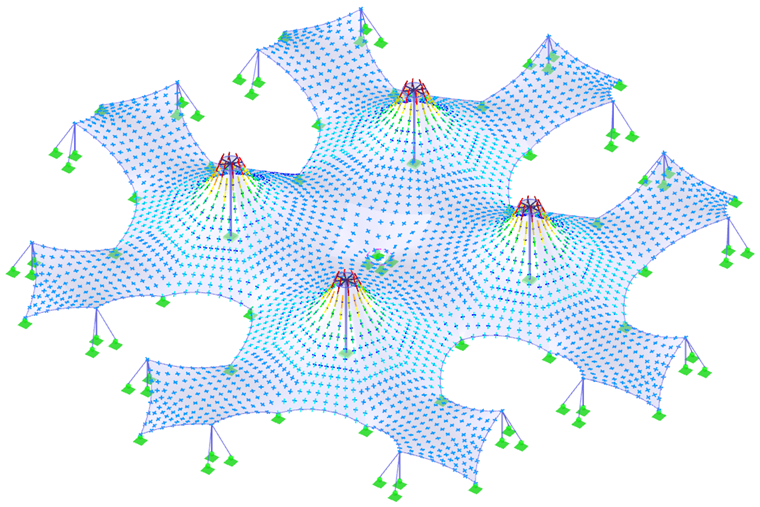
В конце данной главы приводятся еще две сложные конструкции (Рисунок 7 и Рисунок 9) и их предварительные напряжения (Рисунок 8 и Рисунок 10). Для достижения максимально точных результатов в процессе поиска формы, а также при расчете конструкций, необходимо моделировать конструкцию как целое, а не разделять ее на части. Таким образом учитывается взаимодействие всех частей конструкции и перераспределение сил в результате деформаций.
Резка мембранных конструкций
Процесс определения раскройных форм поясняется в следующей статье. В нем описываются отдельные шаги процесса, а затем на практическом примере показано, как свойства материала могут влиять на форму раскройных форм.
Как уже упоминалось, двойная кривизна является одной из характерных черт мембранных конструкций, поэтому ее форма не может возникать в одной плоскости. В то время как мембраны сделаны из рулонов плоской ткани. Для этого должна быть создана раскройная форма, то есть отдельные плоские раскройные формы, которая аппроксимирует свои соответствующие формы в пространстве. Процесс создания раскройной формы состоит из двух шагов. Сначала мембранная конструкция разделяется с помощью линий разреза на отдельные пространственные формы; затем будет найдено наилучшее приближение плоских раскройных форм к пространственным.
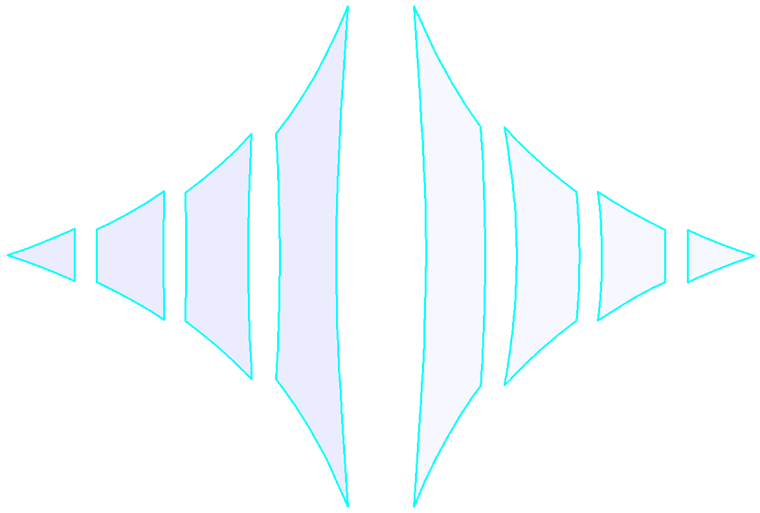
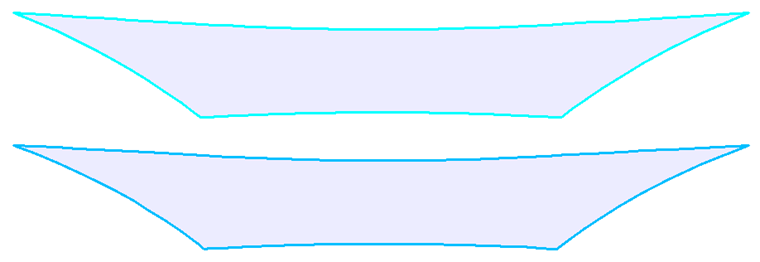
Теоретически мембранную конструкцию можно разделить на частичные полосы любой линией разреза. Однако по практическим причинам обычно используются геодезические линии раскроя (Рисунок 11, слева), которые предпочтительнее из-за прямой оси раскройных форм после выравнивания (Рисунок 12, слева). Плоские профили (Рисунок 11, справа), которые не являются прямыми после выравнивания (Рисунок 12, справа), используются менее часто, и это приводит к более высокому требованию к материалу.
Второй шаг при создании раскройной формы гораздо более сложный: это поиск наилучшего приближения плоской раскройной формы к соответствующей пространственной раскройной форме. Для этого был разработан ряд методов; в самом старом из них использовался упрощенный геометрический метод, а в более поздних методах - расширенное математическое картирование. Актуальные методы затем основаны на механике сплошной среды с нелинейным анализом, использующим метод конечных элементов (МКЭ) для определения раскройной формы.
Последний метод считается наиболее общим решением задачи аппроксимации и позволяет учесть свойства используемого материала ткани или пленки. Если вы не хотите учитывать ортотропные свойства текстильного материала или поперечную усадку, можно применить изотропный материал с коэффициентом Пуассона v = 0. Однако, если свойства материала должны быть включены в процесс Благодаря выравниванию раскройной формы можно достичь оптимальной формы раскройной формы.
При испытании текстильных материалов, используемых для мембранных конструкций, обычно требуется определить жесткость в направлениях основы и утка, а также коэффициент Пуассона. Жесткостью при сдвиге обычно пренебрегают. Следующий пример показывает, как жесткость при сдвиге влияет на форму результирующей раскройной формы. Для примера выберем одну из средних раскройных форм гиперболического параболоида (рисунок 11). Для раскройной формы используются два различных материала.
Для первой ткани с обработанной поверхностью мы получим следующие значения:
EWarp = 1600 кН/м
Eуток = 1200 кН/м
vОснова/уток = 0,05
G = 400 кН/м
Другой материал, текстильная сетка без обработки поверхности, имеет следующие значения:
EWarp = 1600 кН/м
Eуток = 1200 кН/м
vОснова/уток = 0,05
G = 10 кН/м
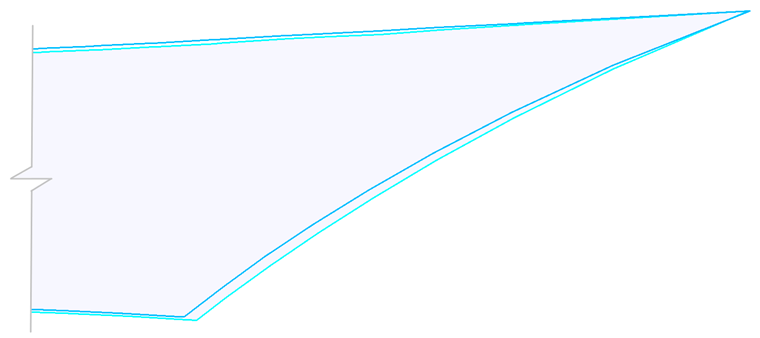
На следующем рисунке показаны полученные раскройные формы. Благодаря перемещению центров тяжести обоих раскройных форм в одну и ту же точку и увеличению правой части раскройных форм в вырезе (рисунок 14), разница между обеими формами становится очевидной. Если учитывать свойства материала, то можно достичь более высокого качества раскройных форм. После монтажа конструкции реальное предварительное напряжение ближе к предполагаемому предварительному напряжению.
Для определения раскройных форм также используется компенсация, которая определяется с помощью двухосных испытаний и имитирует растворение предварительного напряжения в ткани.
Нелинейный расчет по методу конечных элементов позволяет найти энергоэффективную плоскую раскройную форму по отношению к пространственной. Поскольку данный метод расчета основан на физических принципах, он является наиболее естественным.
В процессе создания раскройной формы можно учесть и другие требования к расчёту. Главным образом, требуется соблюдение равной длины смежных краёв смежных раскройных форм. Часто требуется для некоторых краев раскройных форм применить различную компенсацию. Это часто означают как декомпенсацию краев. При соответствии данным требованиям и с помощью нелинейного расчета будет найдена энергоэффективная раскройная форма.
Заключение
Целью этой статьи было объяснение основных процессов, связанных с проектированием мембранных конструкций. Должны быть объяснены физические принципы, а отдельные положения проиллюстрированы примерами. Эти примеры были созданы в программе для расчета конструкций RFEM от компании Dlubal Software GmbH [2].
Благодарим
Данная статья была создана при поддержке проекта FAST-J-15-2803.
Авторы
инж. Ростислав Ланг
doc. инж. инж. Něm Němec, CSc.
инж. Hynek Štekbauser
Институт строительной механики, BUT FCE Брно, МКЭ консалтинг Брно
Оппонент
Prof. Ing. Иржи Студница, доктор наук, Чешский технический университет в Праге
![Основные формы мембранных конструкций [1]](/ru/webimage/009595/2419508/01-png.png)