Die Membrantragwerke gehören zu den heutigen Trends im Bauwesen. Sie zeichnen sich durch ihre Leichtigkeit, beeindruckende Formensprache und effektive Materialausnutzung aus. Infolge ihrer Nullbiegesteifigkeit kann man die Form einer Membrankonstruktion nicht von der Vorspannung trennen. Die Formen sind nicht frei wählbar, sondern sie müssen gefunden werden. Diese formvielfältigen Strukturen werden aus Gewebe- oder Folienrollen gefertigt. Aus ebenen Materialstreifen werden die Schnittmuster gebildet, und indem man sie verbindet und in die finale Lage aufspannt, erreicht man die vorgesehene Konstruktion. Die Zuschnittsermittlung stellt einen empfindlichen Schritt des Planungsprozesses dar, und ihre Qualität beeinflusst stark die Qualität der ganzen Struktur. Der Beitrag wird sich genau mit den zwei Hauptprozessen - mit der Formbestimmung von Membrantragwerken und mit der Ermittlung von Schnittmustern befassen. Besonderes Augenmerk wird auf praktische und für die Planung nutzbare Erkenntnisse gelegt.
Formfindung von Membrankonstruktionen
In diesem Kapitel werden zuerst die physikalischen Grundsätze der Formbestimmung von Membrankonstruktionen beschrieben. Des Weiteren wird die Ausführbarkeit der vom Bauingenieur geforderten Vorspannung behandelt. Im Anschluss wird der Text mit praktischen Beispielen ergänzt, die die Überlegungen und Thesen veranschaulichen sollen.
Die Planung von Membrantragwerken unterscheidet sich deutlich von der üblichen Praxis. Da die verwendeten Materialien praktisch nur eine Zugtragfähigkeit aufweisen, ist die Form nicht frei zu wählen. Man kann die Form nicht von der Vorspannung trennen. In diesem Fall sind ästhetische mit physikalischen Aspekten von Bauwerken grundsätzlich verbunden.
Die Form einer Membrankonstruktion wird durch die Randbedingungen und das räumliche Kräftegleichgewichtssystem bestimmt. Der Formfindungsprozess kann mit der nachstehenden Gleichung (1) beschrieben werden. Die Gleichgewichtsform wird gefunden, wenn sich die virtuelle Arbeit nicht ändert (δW = 0), d.h. wenn die Summe der virtuellen Arbeit, die die geforderte Vorspannung σ verrichtet, und der virtuellen Arbeit, die die äußere Last p (Überdruck, Eigengewicht) leistet, gleich Null ist.
In der oben angeführten Gleichung stellt t die Dicke des verwendeten Materials, δê die Änderung der Materialverformung und δu die Verformung über die Fläche der Struktur Ω dar.
Abgesehen von einigen theoretischen Problemen, die bei der Lösung zu bewältigen sind, gibt es ein weiteres grundlegendes Problem. Das Hauptproblem liegt darin, dass eine im Voraus festgelegte Vorspannung angenommen wird. Die ist jedoch generell ausgeschlossen. Die Membrantragwerke weisen eine doppelte Krümmung auf (d.h. Gaußsche Krümmung ist ungleich Null), weswegen sie eine homogene orthotrope Vorspannung ausschließen. Theoretisch kann somit ein Zustand, wo es in jedem Punkt der Membran einen konkreten Vorspannungswert in Kettrichtung und einen konkreten Vorspannungswert in Schussrichtung gibt, kaum vorliegen. Die einzige Ausnahme stellt die isotrope Vorspannung dar, und die kann man erreichen, wenn die Form unter gegebenen Randbedingungen physikalisch real ist.
Daraus folgt, dass auch nach der Vorspannung selbst gesucht wird. Der Prozess, die sogenannte Formfindung, hat somit zum Ziel, nicht nur eine unbekannte Form für eine vorgegebene Vorspannung zu finden, sondern sie stellt eine Suche nach einer unbekannten Form für eine im Allgemeinen unbekannte Vorspannung dar. Diese Vorspannung wird durch einen vom Bauingenieur vorgegebenen Wert für die Kett- und Schussrichtung angenähert. Für die Formfindung wurde eine Reihe von Methoden entwickelt. Wendet man verschiedene Programme für die Problemlösung an, kann man für dieselben Eingabedaten mehr oder weniger unterschiedliche Ergebnisse erhalten. Dann stellt sich natürlich die Frage ein, welche Lösung die optimale ist. Im Folgenden werden einige Beispiele für verschiedene Strukturen und geforderte Vorspannungen aufgezeigt.
![Grundformen von Membrankonstruktionen [1]](/de/webimage/009595/2267898/01.png?mw=760&hash=18ccf95acbe4a5b802b88236ce3c4d25dbf36a54)
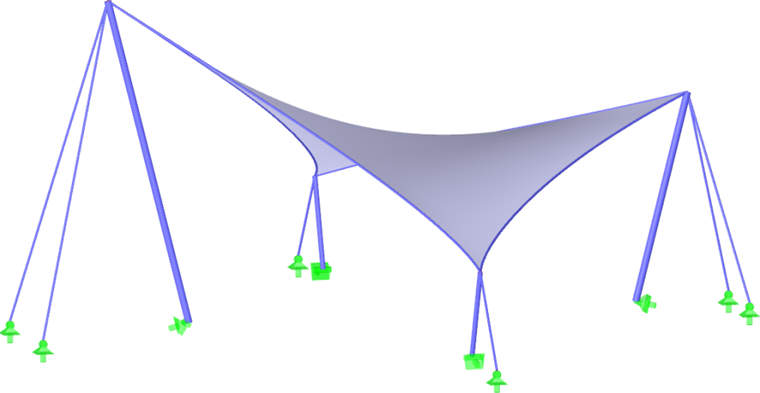
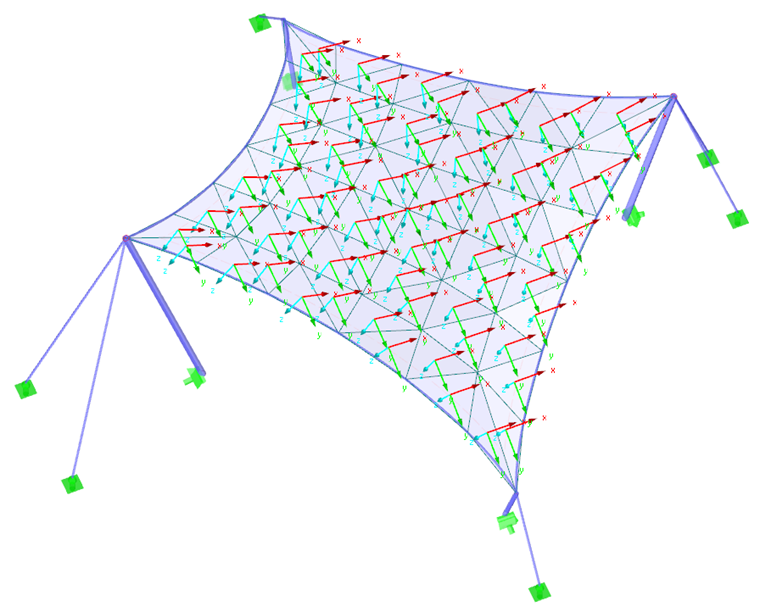
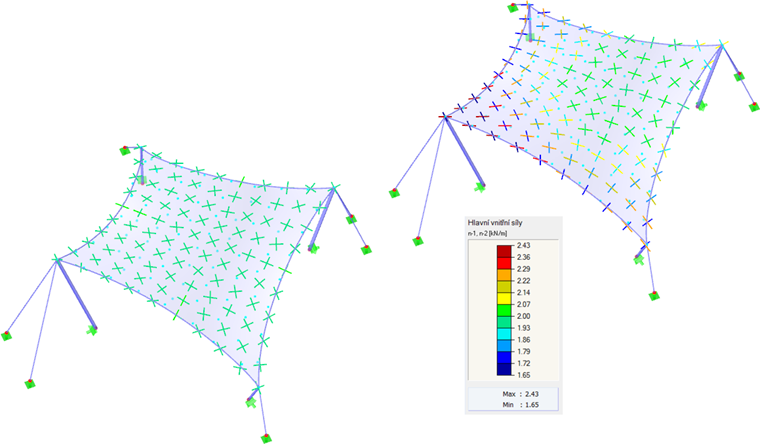
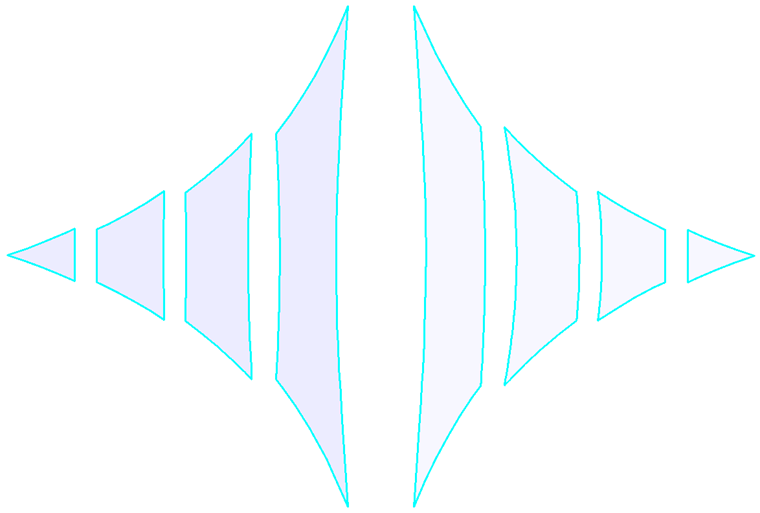
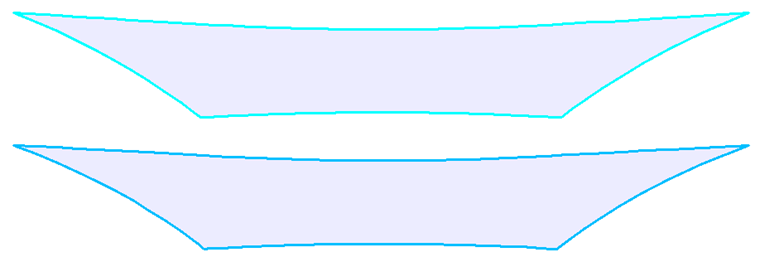
Als erstes Beispiel soll uns ein hyperbolisches Paraboloid dienen (Bild 2 und Bild 3). Es werden sowohl eine isotrope als auch eine orthotrope Vorspannung angesetzt. Für die isotrope Vorspannung ergeben sich aus dem Formfindungsprozess zwei verschiedene Ergebnisse (Bild 4 und Bild 5), die auch kurz kommentiert werden. Für die isotrope Vorspannung stellt man nKette = nSchuss = 2,00 kN/m ein. Für die Randseile stellt man einen relativen Seildurchhang s = 8,00 % ein. Die Ergebnisse werden als Vektoren der Hauptschnittgrößen anhand einer Farbskala veranschaulicht.
Erhält man zwei verschiedene Ergebnisse für dieselben Eingabedaten, dann kommt natürlich die Frage, welche Lösung die richtige ist. Theoretisch sind beide Lösungen richtig, denn beide haben einen Gleichgewichtszustand erzielt und beide sind auch realisierbar. Die links abgebildete Lösung weist jedoch eine gleichmäßige Vorspannung aus, die sich nicht auf Eckbereiche konzentriert. Derartige lokale Effekte sieht man als unerwünscht an, denn sie reduzieren die Tragfähigkeit der Struktur und haben ungleichmäßig wirkende rheologische Effekte zur Folge. Deswegen ist die links angezeigte Lösung vorteilhaft. Generell gilt als günstig, eine Form mit einer gleichmäßig verteilten und nicht lokal konzentrierten Vorspannung zu finden. Die Membrankonstruktion ist somit gut vorgespannt, und ihre Tragfähigkeit wird durch eine übermäßige Vorspannung in einigen Bereichen nicht reduziert.
Wie schon erwähnt, eine isotrope Vorspannung ist die einzige homogene Vorspannung, die man exakt erreichen kann. Die erzielbare Genauigkeit wird praktisch nur durch die Größe des FE-Netzes limitiert. Bei einem grob eingestellten Netz kann ein Gleichgewichtszustand nicht so exakt angenähert werden, und so können die Werte von den eingegebenen Vorspannungen abweichen. Solche Differenzen sollten jedoch in einem kleinen Bereich liegen, wobei ein gröberes Netz auch nicht unbedingt zu einer deutlich konzentrierten Vorspannung führen muss.
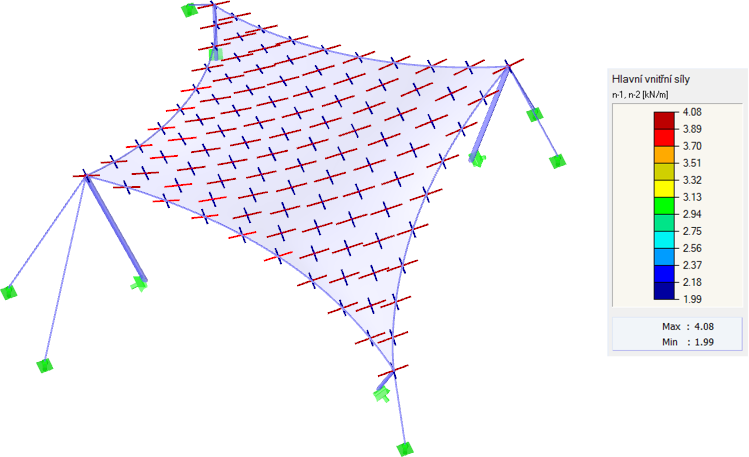
Für die andere Berechnung werden gleiche Randbedingungen angesetzt. Der Konstruktion wird eine orthotrope Vorspannung von nKette = 4,00 kN/m und nSchuss = 2,00 kN/m verliehen. Für die Randseile stellt man einen relativen Seildurchhang s = 8,00 % ein. Wie erwähnt, eine exakte homogene orthotrope Vorspannung kann man wegen der doppelten Krümmung der Membrantragwerke nicht erreichen. Es kann jedoch eine Form mit einer solchen Vorspannung erzielt werden, die den vorgegebenen Werten sehr nahe kommt (Bild 5). Es ergibt sich eine gleichmäßig verteilte Vorspannung, die sich den Eingabewerten annähert. In diesem Fall gibt es keinen Grund für deutliche Spannungskonzentrationen.
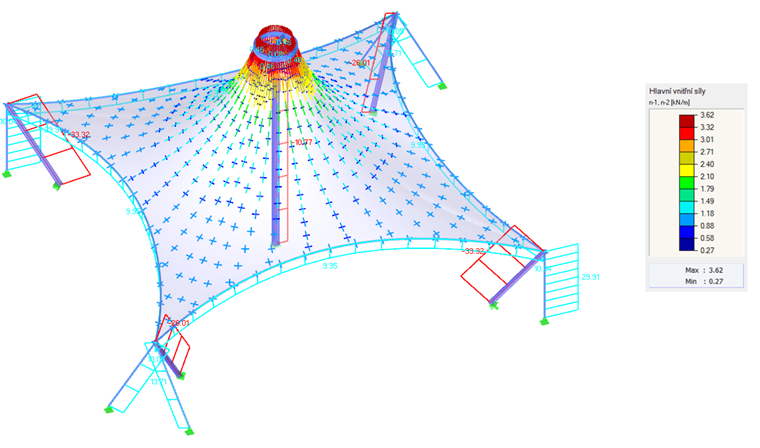
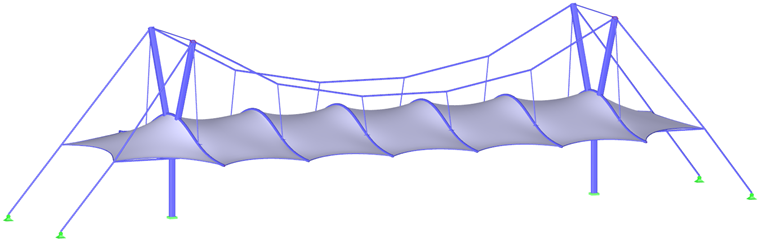
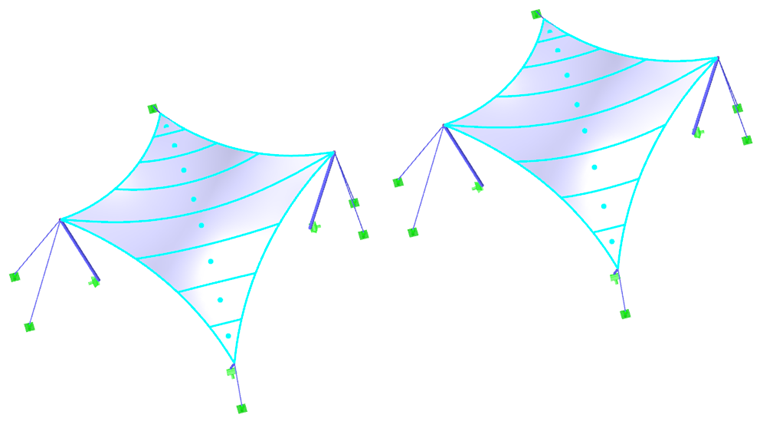
Für die meisten Formen, zu denen zum Beispiel auch hyperbolische Paraboloide, bogengestützte oder pneumatische Membranen zählen (Bild 1), kann die resultierende Vorspannung gleichmäßig verteilt werden, ohne dass lokale Vorspannungskonzentrationen nötig seien. Bei hohen konischen Formen kann man Bereiche mit konzentrierter Vorspannung jedoch nicht vermeiden. Etwaige Konzentrationen treten unerläßlich am Scheitel des Kegels auf, in den unteren Ecken sind sie jedoch weder nötig noch gewünscht (Bild 6).
Ob eine konzentrierte Vorspannung nötig ist, kann man intuitiv aus der folgenden Formel ableiten (2). Die Gleichung stellt ein Kräftegleichgewicht in einem Punkt dar, wobei n1 und n2 die Hauptschnittgrößen, 1/R1 und 1/R2 die Krümmungen in Richtung dieser Hauptschnittgrößen und p etwaige äußere Last sind.
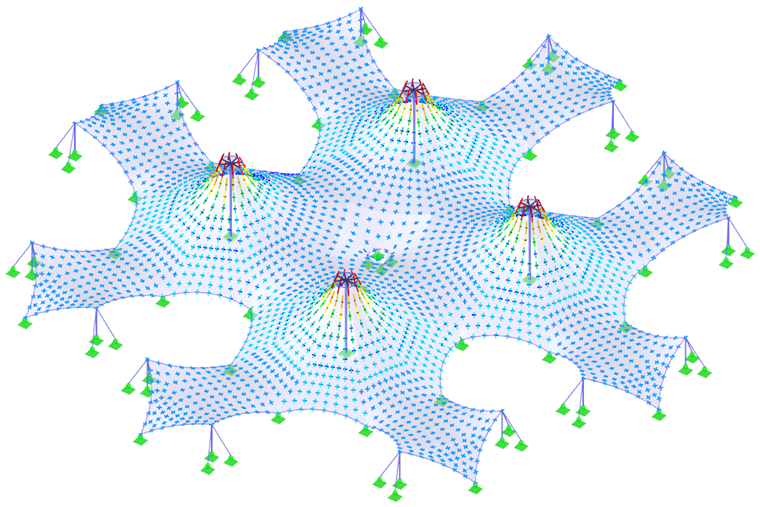
Bei einer antiklastischen Struktur, deren Eigengewicht die gefundene Form kaum beeinflusst, wird das Gleichgewicht der Kräfte in einem Knoten durch die Vorspannung und die gegensinnigen Krümmungen gegeben. Die Frage ist nun, ob sich bei der Struktur die Krümmung so rasant ändern muss. Wenn schon, dann ist die örtlich konzentrierte Vorspannung der Struktur eigen, anderenfalls ist die Konzentration der Vorspannung für die Konstruktion überhaupt nicht nötig. Diese Methode kann man auf unsere Beispiele anwenden. Die Formen ohne konische Bereiche (Bild 4, Bild 5, Bild 8 und Bild 10 außer konischen Bereichen) verlangen keine rasanten Änderungen der Krümmung, weswegen sie gleichmäßig vorgespannt werden können. Konische Bereiche weisen schnelle Änderungen der radialen und tangentialen Krümmungen auf, und daher ist eine schnelle Änderung der Vorspannung nicht zu vermeiden (Bild 6 und konische Bereiche im Bild 10).
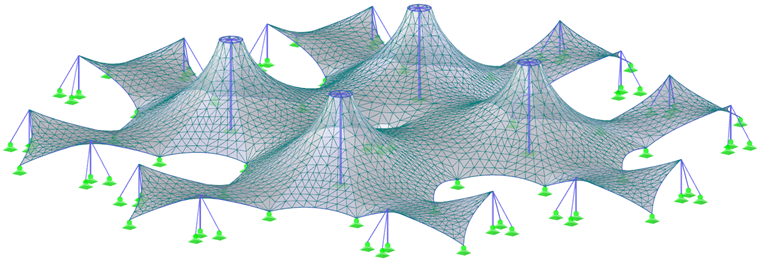
Am Ende dieses Kapitels werden zwei komplexere Strukturen (Bild 7 und Bild 9) und ihre Vorspannungen (Bild 8 und Bild 10) aufgezeigt. Um die möglichst genaue Ergebnisse im Formfindungsprozess sowie auch in der statischen Analyse zu erzielen, soll die Struktur als ein Ganzes und nicht in Teile getrennt modelliert werden. Damit werden ein Zusammenspiel aller Teile der Struktur wie auch die Kräfteumlagerung infolge der Verformungen berücksichtigt.
Zuschnitt von Membrankonstruktionen
Im Folgenden wird der Prozess der Zuschnittsermittlung erläutert. Es werden einzelne Schritte des Prozesses beschrieben, und im Nachgang ein praktisches Beispiel vorgestellt, um aufzuzeigen, wie sich die Materialkennwerte auf die Formen der Schnittmuster auswirken können.
Wie erwähnt, stellt die doppelte Krümmung eine der typischen Merkmale der Membrantragwerke dar, weswegen ihre Form in eine Ebene nicht abgewickelt werden kann. Die Membranen werden jedoch aus Rollen von ebenen Geweben gefertigt. Dafür muss ein Zuschnitt, d.h. einzelne ebene Schnittmuster generiert werden, die sich ihren entsprechenden Mustern im Raum annähern. Der Prozess der Schnittmustererstellung besteht dabei aus zwei Schritten. Zuerst wird die Membrankonstruktion mittels Schnittlinien in einzelne räumliche Zuschnittmuster aufgeteilt, und anschließend wird die bestmögliche Annäherung ebener Schnittmuster an die räumliche gefunden.
Eine Membrankonstruktion kann theoretisch über eine beliebige Schnittlinie in Teilstreifen zerlegt werden. Aus praktischen Gründen werden jedoch meistens geodätische Schnittlinien verwendet (Bild 11 links), die wegen der geraden Achse der Schnittmuster nach der Verebnung vorgezogen werden (Bild 12 links). Weniger oft kommen Ebenenschnitte zur Anwendung (Bild 11 rechts), die nach der Verebnung nicht gerade sind (Bild 12 rechts), und dies hat einen höheren Anspruch an Material zur Folge.
Der zweite Schritt der Schnittmustererstellung ist viel komplexer, in dem die bestmögliche Annäherung eines ebenen Schnittmusters an das entsprechende räumliche Schnittmuster gesucht wird. Für diesen Prozess wurde eine Reihe von Methoden entworfen, von denen die historisch ältesten ein vereinfachtes geometrisches Verfahren und die späteren ein fortgeschrittenes mathematisches Mapping eingesetzt haben. Die aktuellen Methoden sind kontinuumsmechanisch begründet, wobei für die Schnittmusterermittlung eine nichtlineare Analyse unter Verwendung der Finite-Elemente-Methode (FEM) durchgeführt wird.
Die letztgenannte Methode gilt als die generellste Lösung für ein Näherungsproblem und ermöglicht, die Materialkennwerte des verwendeten Gewebes oder der Folie zu berücksichtigen. Will man weder orthotrope Eigenschaften des textilen Materials noch die Querkontraktion in Betracht ziehen, kann man ein isotropes Material mit der Querdehnzahl v = 0 ansetzen. Sollen jedoch die Materialkennwerte in den Prozess der Schnittmusterverebnung mit eingehen, kann eine optimale Form des Schnittmusters erreicht werden.
Beim Testen der textilen Materialien, die für Membrantragwerke verwendet werden, ermittelt man gewöhnlich die Steifigkeiten in Kett- und Schussrichtung und die Querdehnzahl. Die Schubsteifigkeit wird meistens vernachlässigt. Im folgenden Beispiel kann man beobachten, wie sich die Schubsteifigkeit auf die Form des resultierenden Schnittmusters auswirkt. Für das Beispiel haben wir eines der mittleren Schnittmuster des hyperbolischen Paraboloides (Bild 11) gewählt. Für das Schnittmuster werden zwei verschiedene Materialien verwendet.
Für das erste, oberflächenbehandelte Gewebe werden folgende Werte vorgesehen:
EKette = 1600 kN/m
ESchuss = 1200 kN/m
vKette/Schuss = 0,05
G = 400 kN/m
Das andere Material, ein Textilnetz ohne Oberflächenbehandlung, weist folgende Werte auf:
EKette = 1600 kN/m
ESchuss = 1200 kN/m
vKette/Schuss = 0,05
G = 10 kN/m
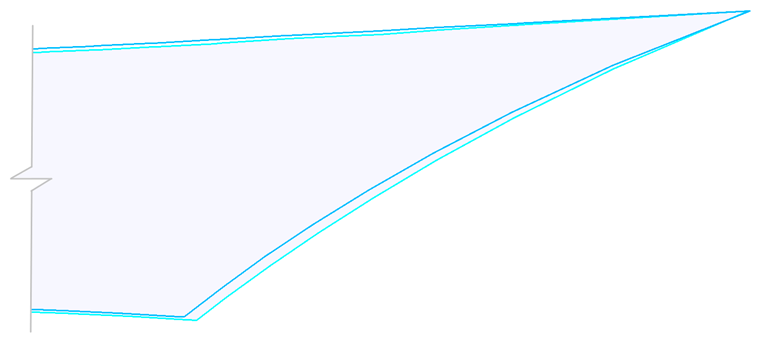
Das folgende Bild zeigt die resultierenden ebenen Schnittmuster. Indem man die Schwerpunkte beider Schnittmuster in denselben Punkt schiebt und den rechten Teil der Schnittmuster im Ausschnitt vergrößert (Bild 14), wird der Unterschied beider Formen deutlich. Berücksichtigt man die Materialkennwerte, können qualitativ bessere Schnittmuster erreicht werden. Nach der Montage des Tragwerkes nähert sich dann die reale Vorspannung an die vorgesehene Vorspannung besser an.
Für die Ermittlung von Schnittmustern wird auch eine Kompensation herangezogen, die durch biaxiale Prüfungen bestimmt wird und die das Auflösen der Vorspannung im Gewebe simuliert.
Eine nichtlineare Berechnung nach der Finite-Elemente-Methode liefert ein energetisch optimales ebenes Schnittmuster in Bezug auf das räumliche. Da von den physikalischen Grundsätzen ausgegangen wird, ist diese Berechnungsmethode die natürlichste.
Im Erstellungsprozess eines Schnittmusters kann man auch andere konstruktive Anforderungen berücksichtigen. Am meisten wird die Erhaltung gleicher Längen der anliegenden Kanten von Nachbarschnittmustern verlangt. Oft wird auch der Ansatz unterschiedlicher Kompensation für einige Ränder von Schnittmustern gefordert. Dies wird häufig als Dekompensation der Ränder bezeichnet. Diesen konstruktiven Anforderungen gerecht und unter Anwendung der nichtlinearen Analyse wird ein energetisch optimiertes Schnittmuster gefunden.
Zusammenfassung
Der Beitrag verfolgte das Ziel, die Hauptprozesse der Planung von Membrantragwerken zu erläutern. Die physikalischen Grundsätze sollten erklärt und die einzelnen Thesen an Beispielen verdeutlicht werden. Die Beispiele wurden im Programm RFEM von Dlubal Software GmbH [2] erarbeitet.
Danksagung
Dieser Beitrag wurde mit Unterstützung des Projekts FAST-J-15-2803 erstellt.
Literatur
Autoren
Ing. Rostislav Lang
doc. Ing. Ivan Němec, CSc.
Ing. Hynek Štekbauser
Institut für Baumechanik, FAST VUT v Brně (Fakultät für Bauingenieurwesen der Technischen Universität Brünn), FEM consulting Brno
Rezensent
Prof. Ing. Jiří Studnička, DrSc., ČVUT v Praze (Tschechische Technische Universität Prag)
.png?mw=350&hash=ee4e41498cc6e20e1c10f0c3c1b6e177b43d290b)
![Grundformen von Membrankonstruktionen [1]](/de/webimage/009595/2267898/01.png?mw=512&hash=cf6341ab051e7b5d63b2a035f430245c5cc92b11)
![Grundformen von Membrankonstruktionen [1]](/de/webimage/009595/2267898/01.png?mw=350&hash=88bb077d881303b0b39a5707520072837a5fcf9e)
.png?mw=350&hash=e3f5898d72f463e9b3e774659aabcb220466c522)
.jpg?mw=350&hash=196d91410dd36f58fcc8b0194f4577bb70cf53c3)
