Les structures à membrane sont l'une des tendances actuelles en génie civil. Elles se caractérisent par leurs formes expression, leur légèreté ou l'utilisation efficace des matériaux. En raison du manque de rigidité en flexion, ces structures ont une forme inséparable à l'état de contrainte.
Il faut donc rechercher leurs formes, qui ne peuvent pas être choisies arbitrairement. Ces structures aux formes et formes différentes sont fabriquées en rouleaux de tissu ou de aluminium. Les patrons de coupe sont formés à partir de bandes de matériaux planes et en les connectant et en les étirant dans la position finale, vous obtenez la structure souhaitée. La détermination des patrons de coupe est une étape sensible du processus de planification et sa qualité influence fortement celle de l'ensemble de la structure.
Cet article traite des deux processus principaux, la détermination de la forme des structures à membrane et la détermination des patrons de coupe. Une attention particulière est accordée aux informations pratiques et utiles pour la planification.
Calcul des structures en toile tendue
Dans ce chapitre, les principes physiques de la détermination des formes pour les structures à membrane sont décrits en premier. De plus, la faisabilité de la précontrainte requise par l'ingénieur civil est abordée. Le texte est ensuite complété par des exemples pratiques afin d'illustrer les considérations et les théories.
La planification des structures à membrane diffère des méthodes habituelles. Les matériaux utilisés n'ayant pratiquement qu'une résistance en traction, la forme ne peut pas être sélectionnée librement. Il est impossible de séparer la forme de la précontrainte. Dans ce cas, les aspects esthétiques et physiques des bâtiments sont fondamentalement connectés.
La forme d'une structure à membrane est déterminée par les conditions aux limites et le système d'équilibre 3D. Le processus de recherche de forme peut être décrit par l'Équation (1) ci-dessous. La forme d'équilibre est trouvée si le travail virtuel ne change pas (δW = 0), c'est-à-dire si la somme du travail virtuel effectuant la précontrainte requise σ et du travail virtuel exécutant la charge externe p (pression positive, poids propre) est égal à zéro.
Dans l'équation ci-dessus, t représente l'épaisseur du matériau utilisé, δêtre la modification de la déformation du matériau et δu la déformation sur la surface de la structure Ω.
Au-delà de quelques problèmes théoriques à résoudre, il y a un problème de fond. Le principal problème est qu'une précontrainte prédéfinie est supposée. Cependant, cette opération est généralement exclue. Les structures à membrane ont une double courbure (c'est-à-dire que la courbure gaussienne n'est pas égale à zéro), c'est pourquoi elles excluent une précontrainte orthotrope homogène. Théoriquement, un état où il existe une valeur de précontrainte spécifique dans la direction de la chaîne et une valeur de précontrainte précise dans la direction de la trame en chaque point de la membrane est presque impossible. La seule exception est la précontrainte isotrope, qui peut être obtenue si la forme est physiquement réelle dans les conditions aux limites données.
La précontrainte elle-même doit donc être trouvée. L'objectif du processus (recherche de forme) n'est pas seulement de trouver une forme inconnue pour une précontrainte donnée, mais également de rechercher une forme inconnue pour une précontrainte généralement inconnue. Cette précontrainte est approximée par une valeur spécifiée par l'ingénieur civil pour les directions de la chaîne et de la trame. Un certain nombre de méthodes ont été développées pour la recherche de forme. Si vous utilisez différents programmes pour la résolution de problèmes, vous pouvez obtenir des résultats plus ou moins différents pour les mêmes données d'entrée. Dans ce cas, la question se pose de savoir quelle solution est la meilleure. Des exemples de différentes structures et des précontraintes requises sont donnés dans les paragraphes ci-dessous.
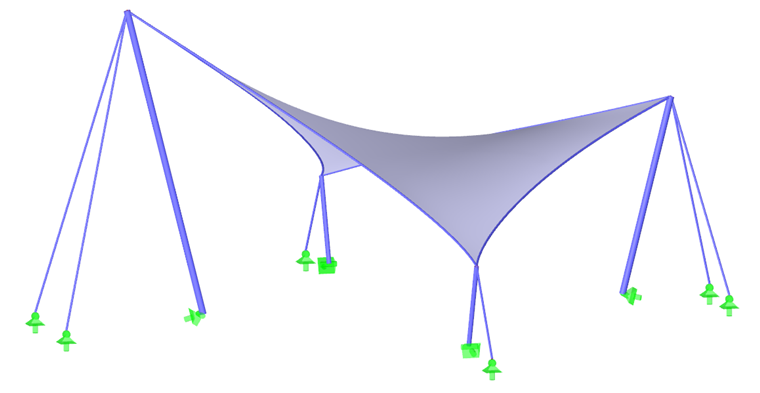
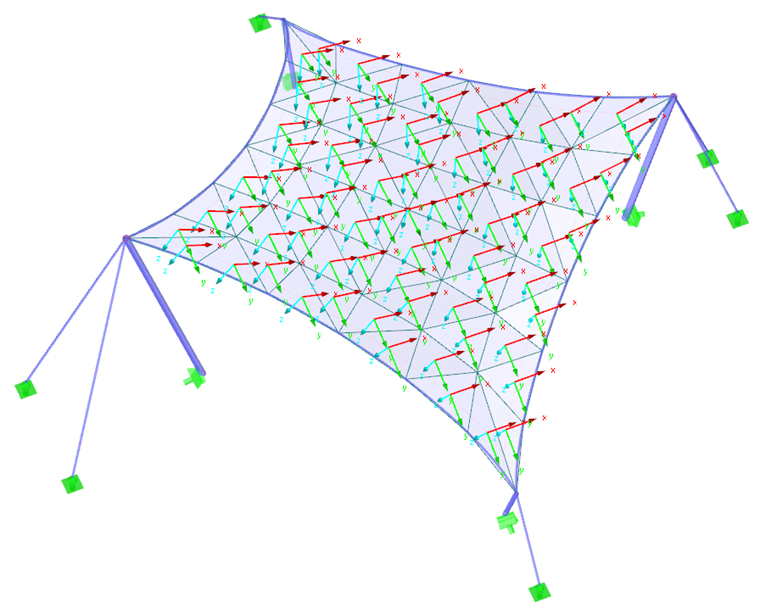
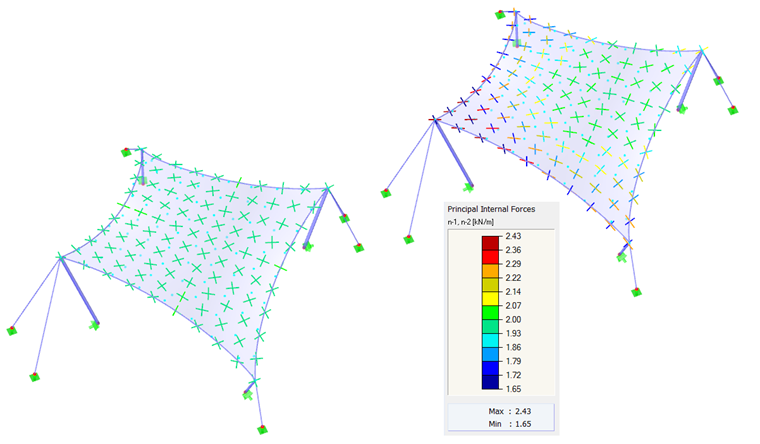
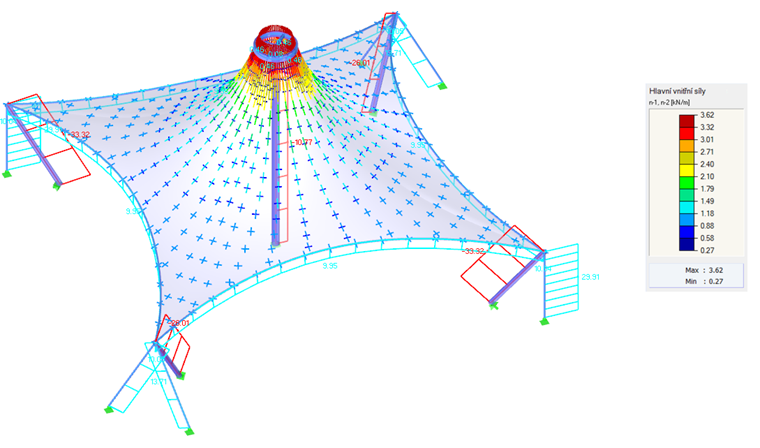
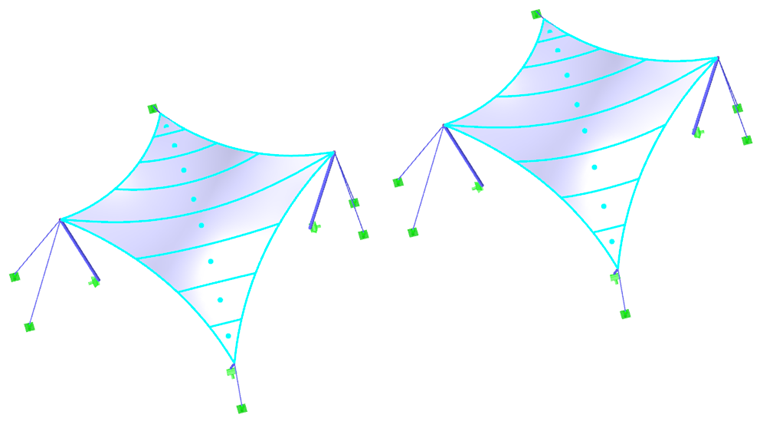
Comme premier exemple, nous allons utiliser un paraboloïde hyperbolique (Figures 2 et Figures 3). Des précontraintes isotropes et orthotropes sont appliquées. Pour la précontrainte isotrope, deux résultats différents résultent de la recherche de forme (Figure 4 et Figure 5), qui sont également brièvement commentés. Les valeurs entrées pour la prétension isotrope sont ngauchissement = ntrame = 2,00 kN/m. Les câbles de périmètre présentent une flèche relative de s = 8,00 %. Les résultats sont affichés sous forme de vecteurs des efforts internes principaux et d'une échelle de couleurs.
Si deux résultats différents sont obtenus pour les mêmes données d'entrée, la question est évidemment de savoir quelle solution est la bonne. Ces deux solutions sont théoriquement correctes car elles ont atteint un état d'équilibre et qu'elles sont également réalistes. Cependant, la solution affichée à gauche montre une précontrainte uniforme qui n'est pas concentrée dans les zones de coin. De tels effets locaux sont considérés comme indésirables car ils réduisent la capacité portante de la structure et entraînent des effets rhéologique inégals. La solution illustrée à gauche est donc avantageuse. Il est généralement considéré comme favorable de trouver une forme avec une précontrainte uniformément répartie et non concentrée localement. La membrane est donc bien précontrainte et sa capacité portante n'est pas réduite dans certaines zones par une précontrainte excessive.
Comme déjà mentionné, une précontrainte isotrope est la seule précontrainte homogène qui puisse être obtenue avec précision. La précision accessible n'est pratiquement limitée que par la taille du maillage EF. Dans le cas d'un maillage grossier, un état d'équilibre ne peut pas être approximé, et les valeurs peuvent donc différer des précontraintes entrées. Cependant, de tels écarts doivent être dans ces limites et un maillage plus grossier ne conduit pas nécessairement à une précontrainte clairement plus concentrée.
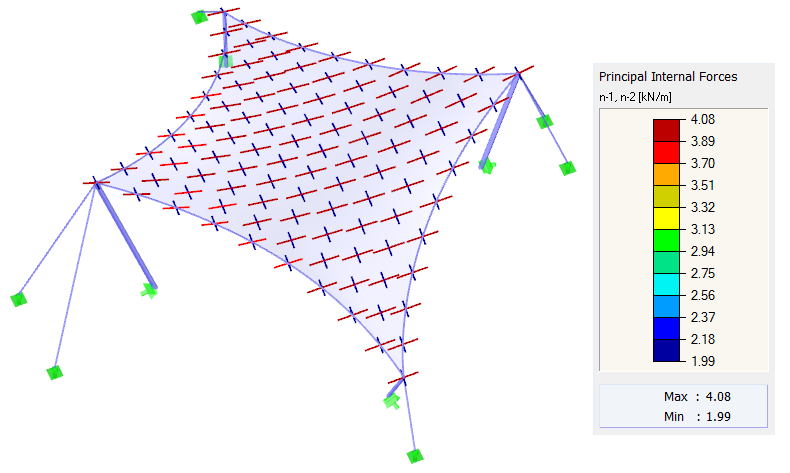
Les mêmes conditions aux limites sont appliquées pour l'autre calcul. La précontrainte est définie comme orthotrope avec n valeurs dela chaîne = 4,00 kN/m et de latrame = 2,00 kN/m. Les câbles de périmètre présentent une flèche relative de s = 8,00 %. Comme mentionné ci-dessus, une précontrainte orthotrope homogène exacte ne peut pas être obtenue car cela n'est théoriquement pas possible avec une double courbure des structures à membrane. Cependant, il est possible d'obtenir une forme avec une précontrainte qui se rapproche étroitement des valeurs spécifiées (Figure 5). Le résultat est une précontrainte uniformément répartie qui correspond presque aux valeurs d'entrée. Avec cette structure, il n'y a aucune raison pour des concentrations importantes.
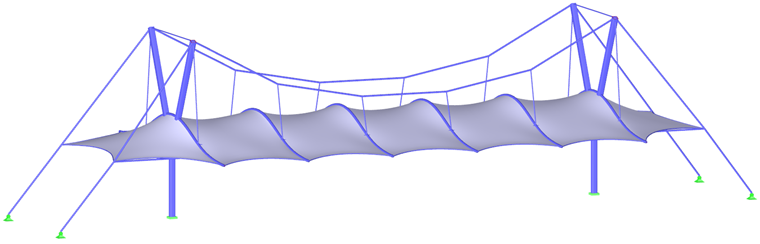
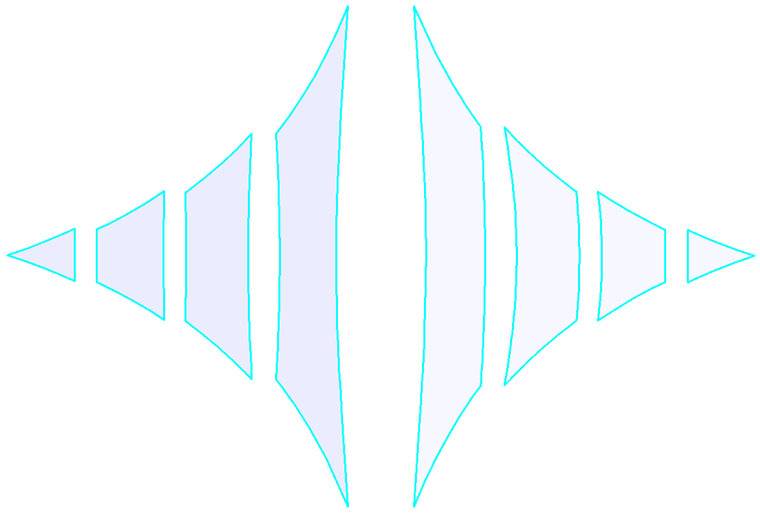
Pour la plupart des formes, y compris les paraboloïde hyperboliques, les membranes tendues ou pneumatiques (Figure 1), la précontrainte résultante peut être répartie uniformément sans avoir besoin de concentrations locales de précontrainte. Pour les grandes formes coniques, il est impossible d'éviter les zones avec une précontrainte concentrée. Les concentrations se produisent au sommet du cône, mais elles ne sont ni nécessaires ni souhaitées dans les coins inférieurs (Figure 6).
Le fait qu'une précontrainte concentrée soit nécessaire ou non peut être déduit de manière intuitive à partir de la formule suivante (2). L'équation représente un équilibre des efforts à un point où n1 et n2 sont les efforts internes principaux, 1/R1 et 1/R2 sont les courbures en direction de ces efforts internes principaux et p est une charge externe.
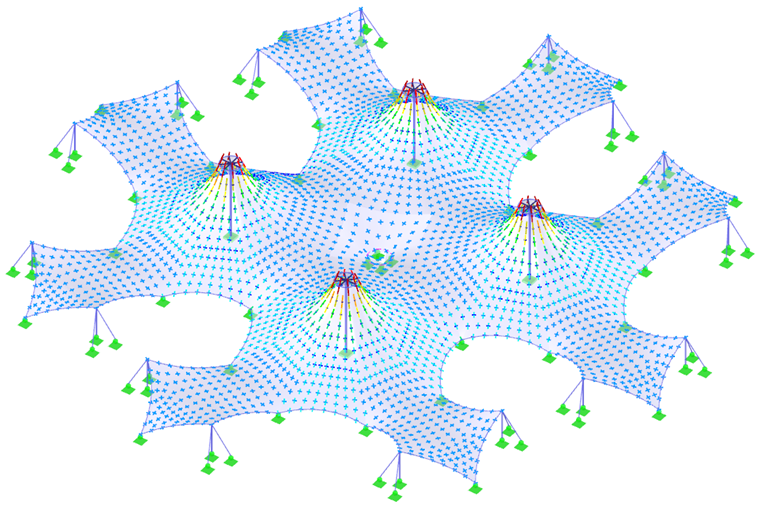
Dans le cas d'une structure anticlastique dont le poids propre n'influence que peu la forme trouvée, l'équilibre des efforts dans un nœud est donné par la précontrainte et les courbures dans la direction opposée. La courbure de la structure doit maintenant être modifiée si rapidement. Si tel est le cas, la précontrainte concentrée localement est propre à la structure ; dans le cas contraire, la concentration de la précontrainte n'est pas nécessaire pour la structure. Cette méthode peut être appliquée à nos exemples. Les formes sans zones coniques (Figure 4, Figure 5, Figure 8 et Figure 10, à l'exception des zones coniques) ne nécessitent pas de modifications rapides de la courbure, c'est pourquoi elles peuvent être précontraintes uniformément. Les zones coniques présentent des modifications rapides des courbures radiales et tangentielles, et une modification rapide de la précontrainte est donc inévitable (Figure 6 et les zones coniques sur la Figure 10).
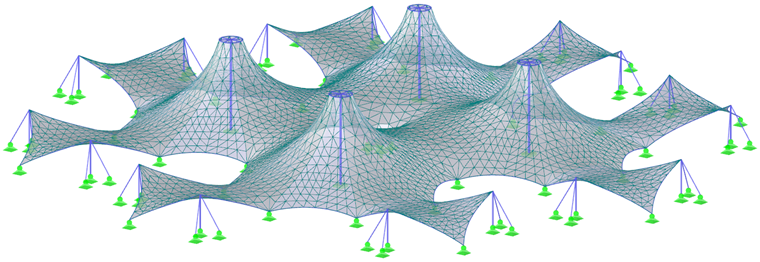
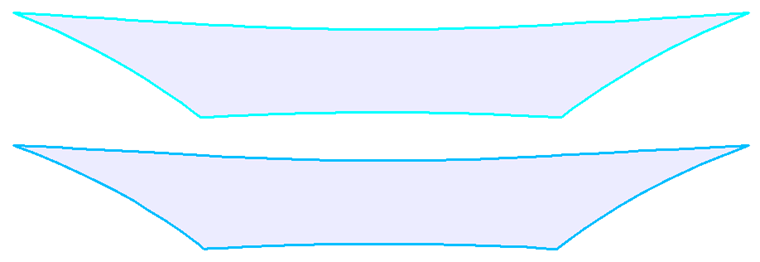
Deux structures plus complexes (Figure 7 et Figure 9) et leurs précontraintes (Figure 8 et Figure 10) sont affichées à la fin de ce chapitre. Afin d'obtenir les résultats les plus précis possible dans le processus de recherche de forme et dans le calcul de structure, la structure doit être modélisée dans son ensemble et non divisée en plusieurs parties. L'interaction de toutes les parties de la structure et la redistribution des efforts due aux déformations sont ainsi considérées.
Structures à membrane de coupe
Le processus de détermination des patrons de coupe est expliqué dans le texte suivant. Il décrit les différentes étapes du processus, puis présente un exemple pratique pour montrer comment les propriétés du matériau peuvent affecter les formes des patrons de coupe.
Comme mentionné précédemment, la double courbure est l'une des caractéristiques typiques des structures à membrane, c'est pourquoi sa forme ne peut pas être développée dans un seul plan. Cependant, les membranes sont composées de rouleaux de toiles 2D. Pour ce faire, une coupe (c'est-à-dire des patrons de coupe plans individuels) doit être générée qui se rapproche de leurs patrons correspondants dans l'espace. La création d'un patron de coupe s'effectue en deux étapes. Tout d'abord, la structure de la membrane est divisée en patrons de coupe 3D individuels à l'aide de lignes de coupe ; ainsi, la meilleure approximation possible des patrons de coupe 2D à 3D est trouvée.
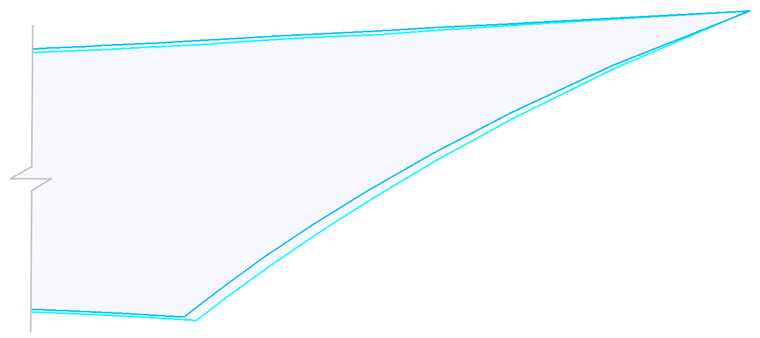
En théorie, une structure textile peut être divisée en plusieurs parties par n'importe quelle ligne de coupe. Pour des raisons pratiques, les lignes de coupe géodésiques sont généralement utilisées (Figure 11, à gauche), qui sont préférées en raison de l'axe droit des patrons de coupe après la mise à plat (Figure 12, à gauche). Les sections planes (Figure 11, à droite) qui ne sont pas droites après la mise à plat (Figure 12, droite) sont utilisées moins souvent, ce qui entraîne des exigences de matériau plus élevées.
La deuxième étape de la création d'un patron de coupe est beaucoup plus complexe : trouver la meilleure approximation possible d'un patron de coupe plan au patron de coupe 3D correspondant. Pour ce processus, un certain nombre de méthodes ont été conçues; les plus anciennes utilisent une méthode géométrique simplifiée et les méthodes ultérieures, un mappage mathématique avancé. Les méthodes actuelles sont basées sur la mécanique du continu, avec une analyse non linéaire selon la méthode des éléments finis (MEF) pour la détermination du patron de coupe.
Cette dernière méthode est considérée comme la solution la plus générale pour un problème d'approximation et vous permet de considérer les propriétés de matériau du tissu ou du film utilisé. Si vous ne souhaitez pas considérer les propriétés orthotropes du matériau textile ou la contraction transversale, vous pouvez appliquer un matériau isotrope avec un coefficient de Poisson v = 0. Cependant, si les propriétés du matériau doivent être incluses dans le processus de la mise à plat du patron de coupe, il est possible d'obtenir la forme optimale du patron de coupe.
Lorsque vous testez des matériaux textiles utilisés pour les structures à membrane, vous déterminez généralement les rigidités dans les directions de gauchissement et de trame ainsi que le coefficient de Poisson. La rigidité de cisaillement est généralement négligée. L'exemple suivant montre l'influence de la rigidité de cisaillement sur la forme du patron de coupe résultant. Pour cet exemple, nous avons sélectionné l'un des patrons de coupe du centre du paraboloïde hyperbolique (Figure 11). Deux matériaux différents sont utilisés pour le patron de coupe.
Les valeurs suivantes sont fournies pour le premier textile traité en surface :
EWarp = 1 600 kN/m
Etrame = 1 200 kN/m
vChaîne/trame = 0,05
G = 400 kN/m
L'autre matériau, un treillis textile sans traitement de surface, a les valeurs suivantes :
EWarp = 1 600 kN/m
Etrame = 1 200 kN/m
vChaîne/trame = 0,05
G = 10 kN/m
La figure suivante affiche les patrons de coupe planes résultants. Si vous déplacez les centres de gravité des deux coupes au même point et que vous agrandissez la partie droite des coupes dans la découpe (Figure 14), la différence entre les deux formes devient claire. Si vous considérez les propriétés du matériau, vous pouvez obtenir des patrons de coupe de meilleure qualité. Une fois la structure assemblée, la précontrainte réelle est plus proche de la précontrainte souhaitée.
Pour la détermination des patrons de coupe, une compensation est également utilisée, qui est déterminée par des tests biaxiaux et simule la disposition de la précontrainte dans le tissu.
Un calcul non linéaire selon la méthode des éléments finis fournit un patron de coupe plan énergétiquement optimal par rapport au modèle 3D. Cette méthode de calcul est la plus naturelle, car elle est basée sur des principes physiques.
Lors de la création d'un patron de coupe, vous pouvez également considérer d'autres exigences de calcul. Il est principalement nécessaire de conserver des longueurs égales des bords adjacents des patrons de coupe adjacents. Très souvent, l’application de compensation différente est requise pour certaines arêtes des patrons de coupe. Elle est souvent décrite comme la décompensation des bords. Conformément à ces exigences de calcul et à l'aide de l'analyse non linéaire, un patron de coupe optimisé énergétiquement est trouvé.
Conclusion
L'objectif de cet article était d'expliquer les processus principaux liés à la planification des structures à membrane. Les principes physiques devraient être expliqués et les thèses individuelles illustrées par des exemples. Ces exemples ont été créés dans le logiciel de calcul RFEM de Dlubal Software [2].
Nous vous remercions
Cet article a été réalisé grâce au support du projet FAST-J-15-2803.
Auteurs
Ingénieurs Rostislav Lang
doc. Ingénieurs Ingénieurs Něm Němec, CSc.
Ingénieurs Hynek Štekbauser
Institut de mécanique des structures, But FCE Brno, FEM Consulting Brno
Superviseur
Prof. Ing. Jiří Studnička, DrSc., Université technique de Prague
![Formes de base des structures à membrane [1]](/fr/webimage/009595/2419504/01-png.png)