Las estructuras con membranas son una de las tendencias actuales en la ingeniería civil. Se caracterizan por sus formas expresivas, ligereza o uso eficiente del material. Debido a la falta de rigidez a flexión, estas estructuras tienen una forma inseparable del estado de tensión.
Esto lleva a la necesidad de buscar sus formas, que no se pueden elegir arbitrariamente. Estas estructuras con diferentes formas están hechas de telas o láminas. Los patrones de corte se forman a partir de tiras de material planas, y se logra la estructura deseada al conectarlas y estirarlas en la posición final. La determinación de los patrones de corte es un paso sensible en el proceso de planificación, y su calidad influye fuertemente en la calidad de toda la estructura.
Este artículo trata en detalle los dos procesos principales: la determinación de la forma de las estructuras de membrana y la determinación de los patrones de corte. Se presta especial atención a los conocimientos prácticos y útiles para la planificación.
Diseño de estructuras con membranas
En este capítulo, se describen primero los principios físicos de la determinación de la forma para estructuras con membranas. Además, se analiza la viabilidad del pretensado requerido por el ingeniero de estructuras. El texto se complementa con ejemplos prácticos para ilustrar las consideraciones y teorías.
La planificación de las estructuras con membranas difiere significativamente de la práctica habitual. Dado que los materiales utilizados prácticamente solo tienen una resistencia a tracción, la forma no se puede seleccionar libremente. No es posible separar la forma del pretensado. En este caso, los aspectos estéticos y físicos de los edificios están básicamente conectados.
La forma de una estructura con membranas está determinada por las condiciones de contorno y el sistema de equilibrio espacial. El proceso de búsqueda de forma se puede describir mediante la ecuación (1) a continuación. La forma de equilibrio se encuentra si el trabajo virtual no cambia (δW = 0); es decir, si la suma del trabajo virtual que realiza el pretensado requerido σ y el trabajo virtual que realiza la carga externa p (presión positiva, peso propio) es igual a cero.
En la ecuación anterior, t representa el espesor del material utilizado, δê es el cambio en la deformación del material y δu es la deformación sobre la superficie de la estructura Ω.
Además de algunos problemas teóricos a resolver, hay un problema fundamental. El problema principal es que se asume un pretensado preestablecido. Sin embargo, generalmente se excluye. Las estructuras con membranas tienen una doble curvatura (es decir, la curvatura gaussiana no es igual a cero), por lo que excluyen un pretensado ortótropo homogéneo. Teóricamente, es casi imposible un estado donde haya un valor de pretensado específico en la dirección de la urdimbre y un valor de pretensado preciso en la dirección de la trama en cada punto de la membrana. La única excepción es el pretensado isótropo, que se puede lograr si la forma es físicamente real bajo las condiciones de contorno proporcionadas.
Por lo tanto, se debe encontrar el pretensado en sí. El objetivo del proceso (búsqueda de forma) no es solo encontrar una forma desconocida para un pretensado proporcionado, sino también buscar una forma desconocida para un pretensado generalmente desconocido. Este pretensado se aproxima mediante un valor especificado por el ingeniero de estructuras para las direcciones de la urdimbre y la trama. Se han desarrollado varios métodos para la búsqueda de la forma. Si utiliza diferentes programas para resolver problemas, puede obtener resultados más o menos diferentes para los mismos datos de entrada. Entonces, por supuesto, surge la pregunta de qué solución es la óptima. A continuación se muestran algunos ejemplos de diferentes estructuras y pretensados requeridos.
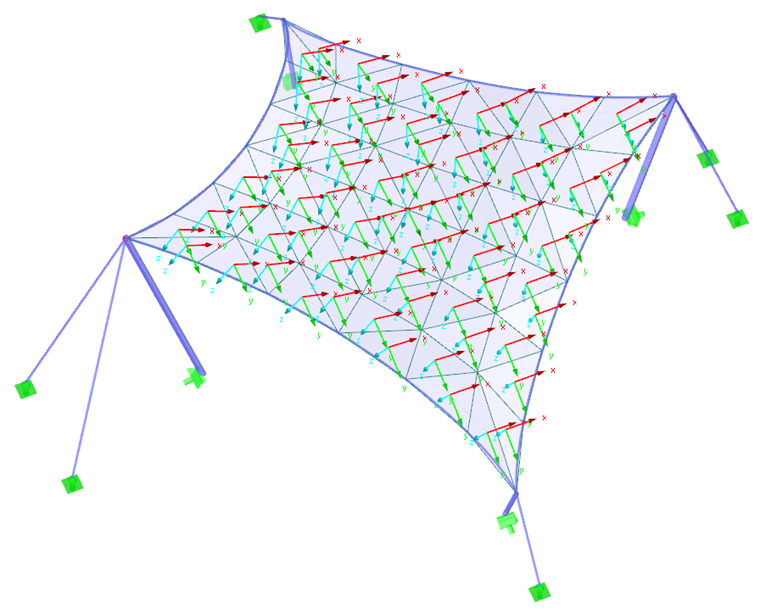
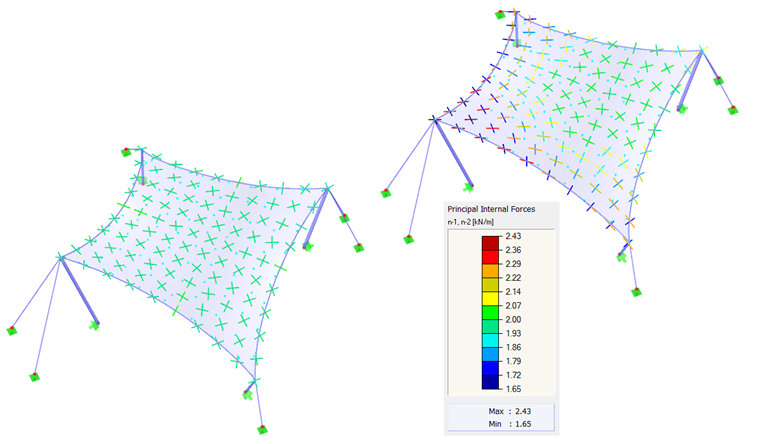
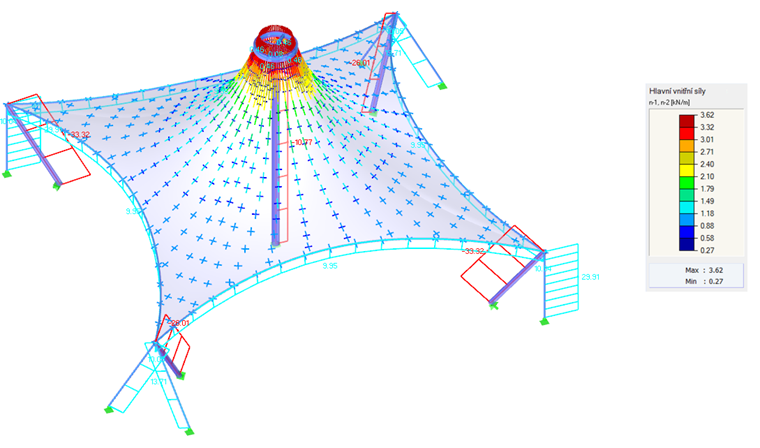
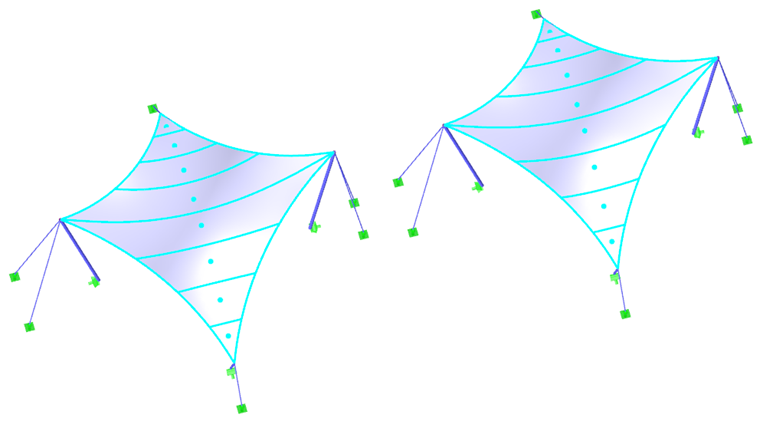
Como primer ejemplo, usaremos un paraboloide hiperbólico (imágenes 02 y 03). Se aplica tanto el pretensado isótropo como el orótropo. Para el pretensado isótropo, se obtienen dos resultados diferentes del proceso de búsqueda de forma (imágenes 4 y 5), que también se comentan brevemente. Los valores introducidos para el pretensado isótropo son nurdimbre = ntrama = 2,00 kN/m. Los cables perimetrales tienen una flecha relativa de s = 8,00%. Los resultados se muestran como vectores de los esfuerzos internos principales y una escala de colores.
Si se obtienen dos resultados diferentes para los mismos datos de entrada, surge naturalmente la pregunta de qué solución es la correcta. En teoría, ambas soluciones son correctas porque ambas han alcanzado un estado de equilibrio y ambas son factibles. Sin embargo, la solución que se muestra a la izquierda muestra un pretensado uniforme que no se concentra en las áreas de las esquinas. Tales efectos locales se consideran indeseables porque reducen la capacidad de carga de la estructura y dan como resultado efectos reológicos desiguales. Por lo tanto, la solución que se muestra a la izquierda es ventajosa. Generalmente, se considera favorable encontrar una forma con un pretensado distribuido uniformemente y no concentrado localmente. Por lo tanto, la estructura de la membrana está bien pretensada y su capacidad de carga no se reduce en algunas áreas por un pretensado excesivo.
Como ya se mencionó, un pretensado isótropo es el único pretensado homogéneo que se puede lograr con precisión. La precisión alcanzable está limitada prácticamente solo por el tamaño de la malla de elementos finitos (EF). En el caso de una malla más gruesa, no se puede aproximar exactamente un estado de equilibrio y, por lo tanto, los valores pueden desviarse de los pretensados introducidos. Sin embargo, tales desviaciones deberían estar dentro de un rango pequeño, y una malla más gruesa no conduce necesariamente a un pretensado claramente más concentrado.
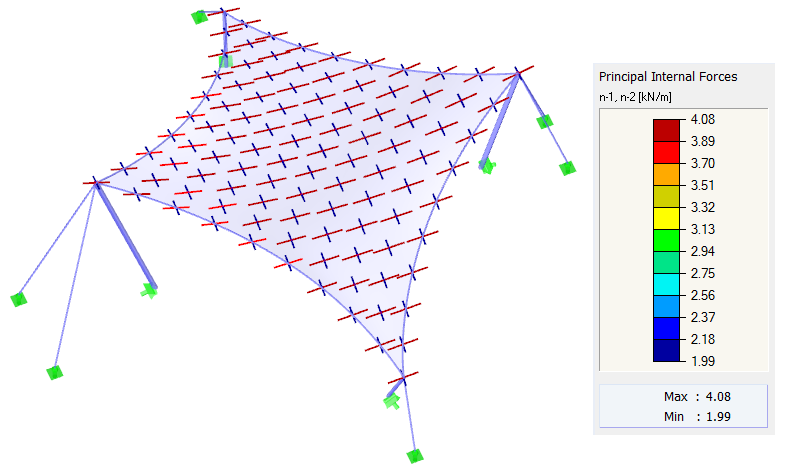
Se aplican las mismas condiciones de contorno para el otro cálculo. El pretensado se define como ortótropo con los valores nurdimbre = 4,00 kN/m y ntrama = 2,00 kN/m. Los cables perimetrales tienen una flecha relativa de s = 8,00%. Como se mencionó anteriormente, no se puede lograr un pretensado ortótropo homogéneo exacto, porque esto no es teóricamente posible con la doble curvatura de las estructuras con membranas. Sin embargo, es posible obtener una forma con un pretensado que se aproxime mucho a los valores especificados (Imagen 5). El resultado es un pretensado uniformemente distribuido que se aproxima a los valores de entrada. En el caso de una estructura de este tipo, no hay razón para concentraciones significativas.
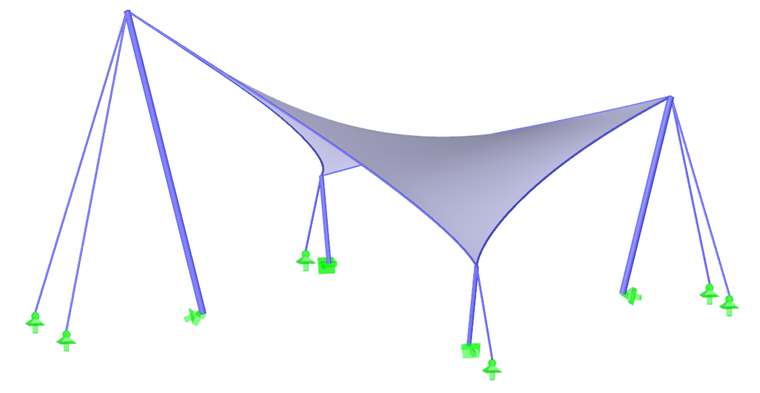
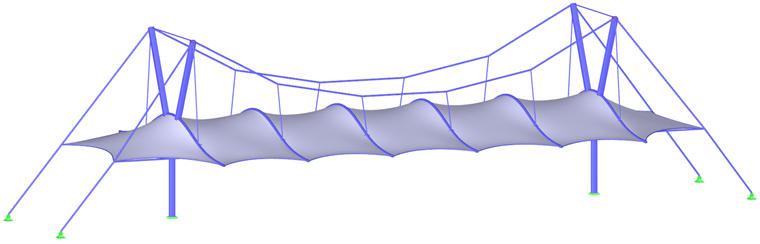
Para la mayoría de las formas, incluidos los paraboloides hiperbólicos o las membranas neumáticas o apoyadas en arco (imagen 1), el pretensado resultante se puede distribuir uniformemente sin la necesidad de concentraciones de pretensado locales. Para formas cónicas altas, no es posible evitar áreas con pretensado concentrado. Cualquier concentración ocurre en el vértice del cono, pero no es necesaria ni deseada en las esquinas inferiores (imagen 06).
Si se necesita o no un pretensado concentrado se puede deducir intuitivamente de la siguiente fórmula (2). La ecuación representa un equilibrio de fuerzas en un punto donde n1 y n2 son los esfuerzos internos principales, 1/R1 y 1/R2 son las curvaturas en la dirección de estos esfuerzos internos principales, y p es cualquier carga externa.
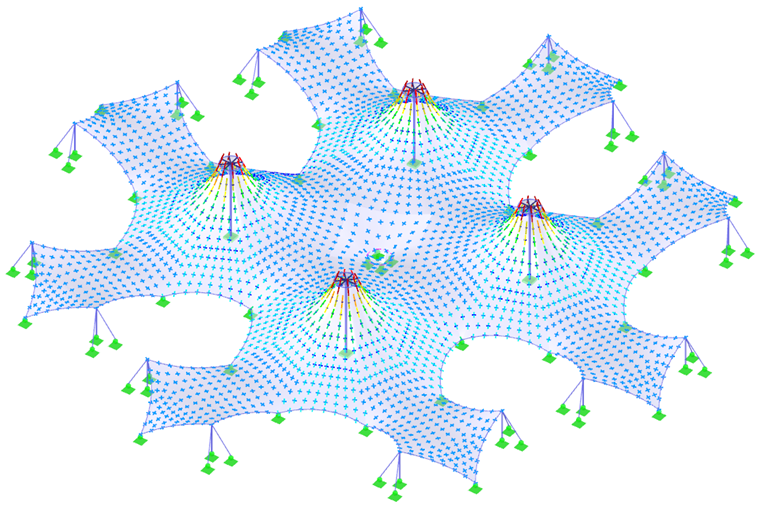
En el caso de una estructura anticlástica cuyo peso propio apenas influye en la forma encontrada, el equilibrio de fuerzas en un nudo viene dado por el pretensado y las curvaturas en la dirección opuesta. La cuestión ahora es si la curvatura de la estructura tiene que cambiar tan rápidamente. Si es así, el pretensado concentrado localmente es inherente a la estructura; de lo contrario, la concentración de pretensado no es necesaria para esta. Este método se puede aplicar a nuestros ejemplos. Las formas sin áreas cónicas (imágenes 4, 5, 8 y 10, excepto las áreas cónicas) no requieren cambios rápidos en la curvatura, por lo que se pueden pretensar uniformemente. Las áreas cónicas muestran cambios rápidos de las curvaturas radial y tangencial y, por lo tanto, no se puede evitar un cambio rápido del pretensado (imagen 6 y áreas cónicas en la imagen 10).
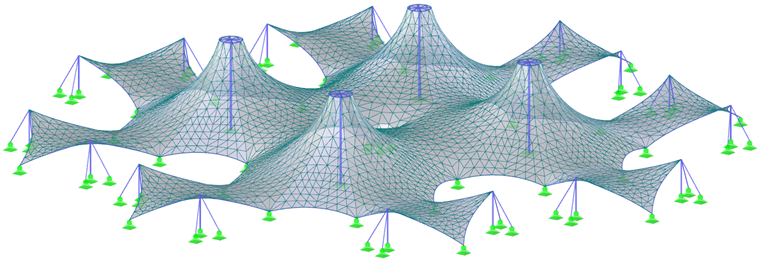
Al final de este capítulo se muestran dos estructuras más complejas (imágenes 7 y 9) y sus pretensados (imágenes 8 y 10). Para lograr los resultados más precisos posibles en el proceso de búsqueda de forma, así como en el análisis estructural, la estructura se debe modelar como un todo y no por partes. Por lo tanto, se considera la interacción de todas las partes de la estructura y la redistribución de esfuerzos debido a las deformaciones.
Corte de estructuras con membranas
El proceso para determinar los patrones de corte se explica en el siguiente texto. Describe los pasos individuales del proceso y luego presenta un ejemplo práctico para mostrar cómo las propiedades del material pueden afectar las formas de los patrones de corte.
Como se mencionó, la doble curvatura es una de las características típicas de las estructuras con membranas, por lo que su forma no se puede desarrollar en un plano. Sin embargo, las membranas están hechas de rollos de tejidos planos. Para esto, se debe generar un corte (es decir, patrones de corte planos individuales) que se aproxime a sus patrones correspondientes en el espacio. El proceso de creación de un patrón de corte consta de dos pasos. Primero, la estructura de la membrana se divide en patrones de corte espacial individuales por medio de líneas de corte; luego, se encuentra la mejor aproximación posible de los patrones de corte planos al espacial.
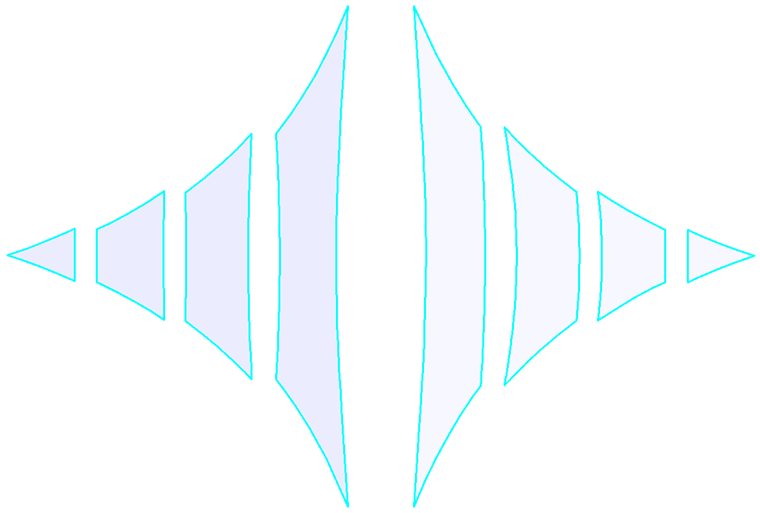
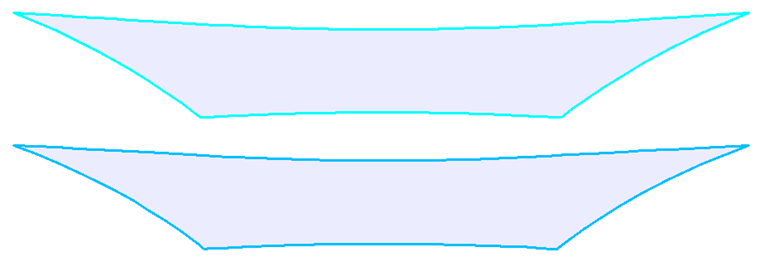
En teoría, una estructura con membranas se puede dividir en tiras parciales por cualquier línea de corte. Sin embargo, por razones prácticas, generalmente se usan líneas de corte geodésicas (imagen 11, izquierda), que se prefieren debido al eje recto de los patrones de corte después del aplanamiento (figura 12, izquierda). Las secciones planas (imagen 11, derecha) que no son rectas después del aplanamiento (imagen 12, derecha) se usan con menos frecuencia, y esto da como resultado un mayor requisito de material.
El segundo paso de la creación de un patrón de corte es mucho más complejo: encontrar la mejor aproximación posible de un patrón de corte plano al patrón de corte espacial correspondiente. Para este proceso, se diseñaron varios métodos; el más antiguo históricamente utilizó un método geométrico simplificado y los métodos posteriores, un mapeo matemático avanzado. Los métodos actuales se basan en la mecánica continua, con un análisis no lineal utilizando el método de elementos finitos (MEF) para la determinación del patrones de corte.
El último método se considera la solución más general para un problema de aproximación y le permite considerar las propiedades del material de la tela o lámina utilizada. Si no desea considerar las propiedades ortótropas del material textil o la contracción transversal, puede aplicar un material isótropo con el coeficiente de Poisson v = 0. Sin embargo, si se van a incluir las propiedades del material en el proceso de aplanado del patrón de corte, se puede lograr su forma óptima.
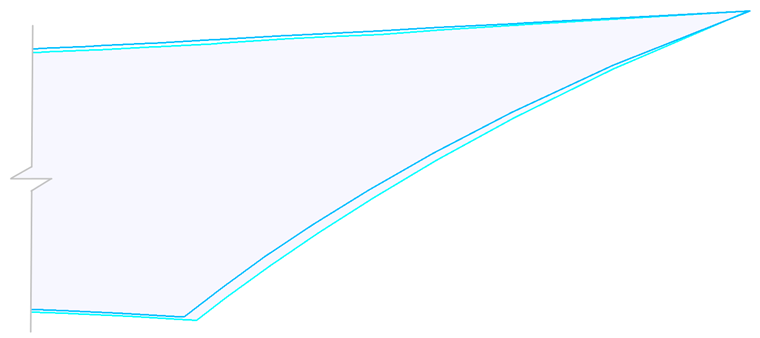
Cuando se prueban los materiales textiles utilizados para estructuras con membranas, usted determina normalmente las rigideces en las direcciones de la urdimbre y la trama, y el coeficiente de Poisson. Normalmente se omite la rigidez a cortante. El siguiente ejemplo muestra cómo la rigidez a cortante afecta la forma del patrón de corte resultante. Para el ejemplo, hemos seleccionado uno de los patrones de corte medio del paraboloide hiperbólico (imagen 11). Se utilizan dos materiales diferentes para el patrón de corte.
Se proporcionan los siguientes valores para la primera tela tratada superficialmente:
Ealabeo = 1.600 kN/m
Etrama = 1.200 kN/m
vurdimbre/trama = 0,05
G = 400 kN/m
El otro material, una malla textil sin tratamiento superficial, tiene los siguientes valores:
Ealabeo = 1.600 kN/m
Etrama = 1.200 kN/m
vurdimbre/trama = 0,05
G = 10 kN/m
La siguiente imagen muestra los patrones de corte planos resultantes. Al mover los centros de gravedad de ambos patrones de corte en el mismo punto y ampliar la parte derecha de los patrones de corte en el recorte (Imagen 14), la diferencia entre ambas formas se vuelve clara. Si considera las propiedades del material, puede lograr patrones de corte de mejor calidad. Después de ensamblar la estructura, el pretensado real está más cerca del pretensado previsto.
Para la determinación de los patrones de corte, también se utiliza una compensación, que se determina mediante pruebas biaxiales y simula la disolución del pretensado en el tejido.
Un cálculo no lineal según el método de elementos finitos proporciona un patrón de corte plano energéticamente óptimo en relación con el espacial. Dado que se basa en principios físicos, este método de cálculo es el más natural.
En el proceso de creación de un patrón de corte, también puede considerar otros requisitos de diseño. Principalmente, se requiere mantener las longitudes iguales de los bordes adyacentes de los patrones de corte adyacentes. A menudo, se requiere la aplicación de una compensación diferente para algunos bordes de los patrones de corte. Esto a menudo se conoce como descompensación de los bordes. Cumpliendo con estos requisitos de diseño y utilizando el análisis no lineal, se encuentra un patrón de corte energéticamente optimizado.
Conclusión
El objetivo de este artículo fue explicar los principales procesos relacionados con la planificación de estructuras con membranas. Se explican los principios físicos y las tesis individuales ilustradas con ejemplos. Estos ejemplos se crearon en el software de ingeniería RFEM de Dlubal Software GmbH [2].
Agradecimientos
Este artículo fue creado con el apoyo del proyecto FAST-J-15-2803.
Autores
Ing. Rostislav Lang
doc. Ing. Ivan Němec, CSc.
Ing. Hynek Stekbauser
Instituto de Mecánica Estructural, BUT FCE Brno, FEM consulting Brno
Verificador
Prof. Ing. Jiří Studnička, DrSc., Universidad Técnica Checa en Praga (ČVUT)
![Formas básicas de estructuras de membranas [1]](/es/webimage/009595/2419503/01-png.png)