Zurück zu Online-Handbüchern

540x

004088

28. September 2023

Handbuch wählen

Übersicht

Einführung

Berechnung

Finite Elemente

Materialnichtlinearität

Wenn die Ergänzung zur Analyse des nichtlinearen Materialverhaltens (Lizenz erforderlich) in den Modell - Basisdaten aktiviert ist, gibt es in der Liste der Materialmodelle weitere Auswahlmöglichkeiten zusätzlich zu den Materialmodellen "Isotrop | Linear Elastisch" und "Orthotrop | Linear Elastisch".

Materialmodelle für Analyse-Add-On 'Nichtlineares Materialverhalten'

Wenn Sie nichtlineare Materialmodelle in RFEM verwenden, wird immer eine iterative Berechnung durchgeführt. Je nach Materialmodell wird eine unterschiedliche Beziehung zwischen den Spannungen und Dehnungen definiert.

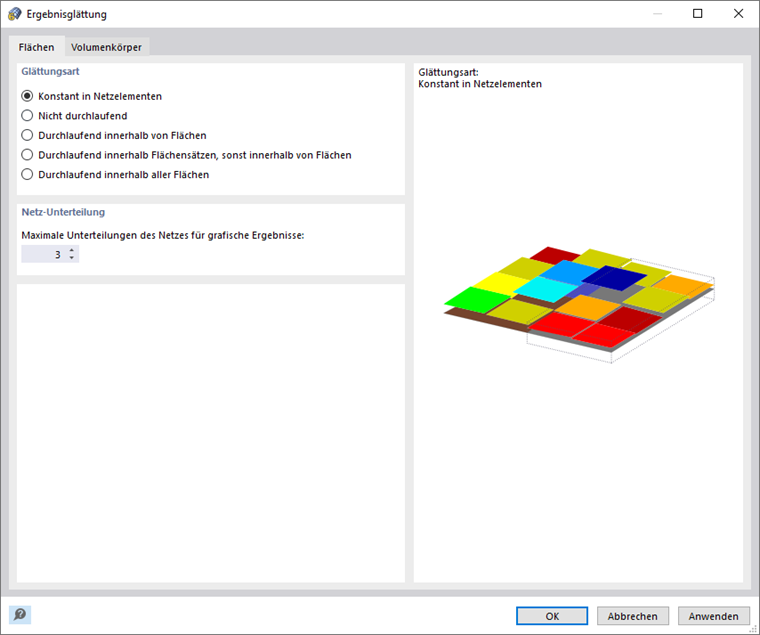
Die Steifigkeit der Finiten-Elemente wird im Laufe der Iterationen immer wieder angepasst, bis die Spannungs-Dehnungs-Beziehung erfüllt ist. Die Anpassung erfolgt immer für eine gesamte Fläche oder Volumenelement. Daher empfehlen wir, bei der Bewertung von Spannungen immer den Glättungstyp "Konstant auf Netzelementen" zu verwenden.

Ergebnisglättung

Einige Materialmodelle in RFEM sind mit "Plastisch" gekennzeichnet, andere mit "Nichtlinear Elastisch".

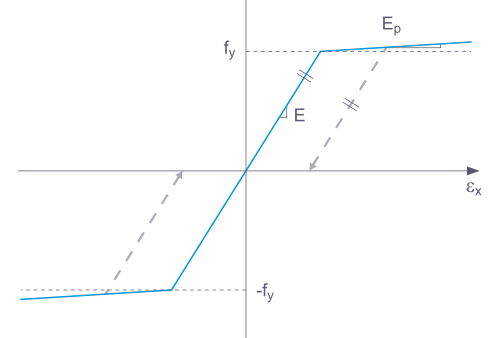
Wenn ein Bauteil mit einem nichtlinear elastischen Material erneut entlastet wird, geht die Dehnung auf demselben Weg zurück. Bei vollständiger Entlastung ist keine Dehnung mehr vorhanden.

Spannungs-Dehnungs-Diagramm nichtlinear elastisch

Bei der Entlastung eines Bauteils mit einem plastischen Materialmodell bleibt die Dehnung nach vollständiger Entlastung bestehen.

Spannungs-Dehnungs-Diagramm plastisch

Hintergrundinformationen über nichtlineare Materialmodelle finden Sie im technischen Artikel, der die Fließgesetze im isotropen nichtlinearen elastischen Materialmodell beschreibt.

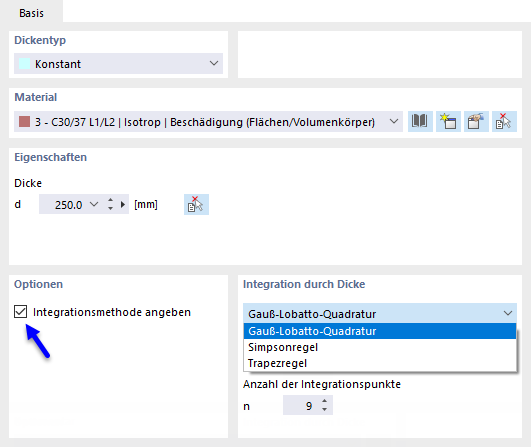
Die inneren Kräfte und Momente in Platten mit nichtlinearem Material resultieren aus der numerischen Integration der Spannungen über die Dicke d der Platte. Um die Integrationsmethode für die Dicke zu definieren, wählen Sie die Option "Integrationsmethode angeben" im Dialogfeld "Dicke bearbeiten". Folgende Integrationsmethoden stehen zur Verfügung:

Gauss-Lobatto-Quadratur
Simpsons Regel
Trapezregel

Integrationsmethode für Flächendicke festlegen

Des Weiteren können Sie die "Anzahl der Integrationspunkte" von 3 bis 99 nach der Plattenstärke spezifizieren.

Info

Eine theoretische Erklärung der einzelnen Integrationsmethoden finden Sie im Online-Handbuch für Mehrschichtige Flächen.

Isotrop Plastisch | Stäbe

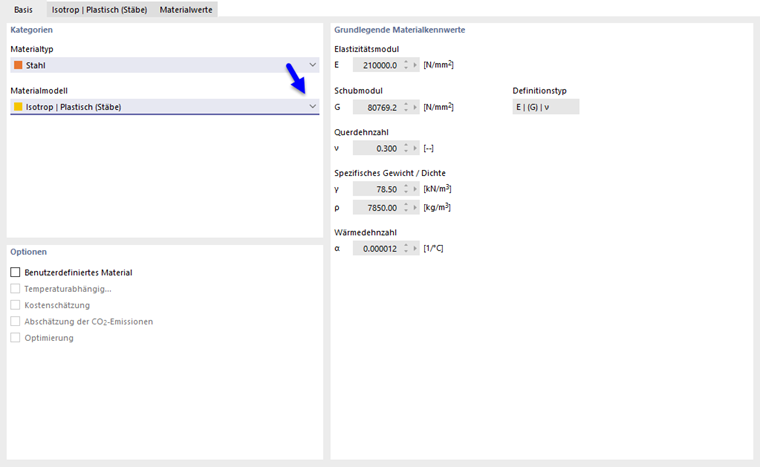
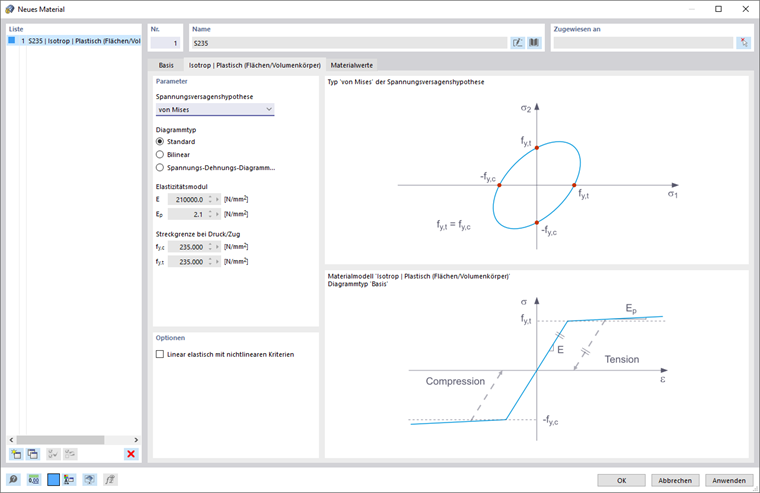
Beim Auswählen des Eintrags Isotrop | Plastisch (Stäbe) im Dropdown-Menü "Materialmodell" wird der Reiter zum Eingeben der nichtlinearen Materialparameter aktiviert.

Nichtlineares Materialmodell aktivieren

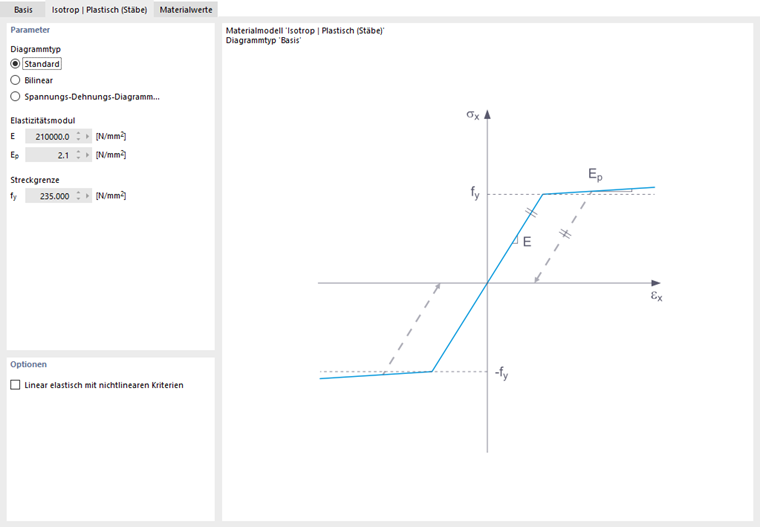
Nichtlineare Materialparameter definieren

In diesem Reiter definieren Sie das Spannungs-Dehnungs-Diagramm. Folgende Optionen stehen zur Verfügung:

Grundlegend
Bilingual
Spannungs-Dehnungs-Diagramm

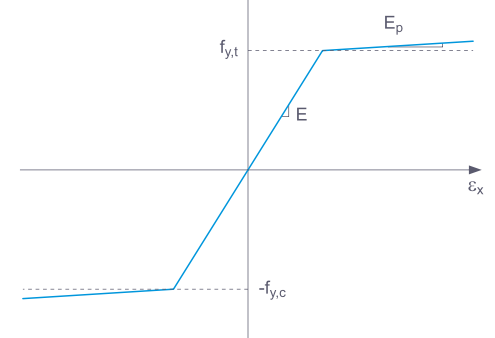
Wenn Grundlegend ausgewählt ist, verwendet RFEM ein bilineares Materialmodell. Werte aus der Materialdatenbank werden für den Elastizitätsmodul E und die Streckgrenze f_y verwendet. Aus numerischen Gründen ist der Verlauf des Diagramms nicht genau horizontal, sondern hat eine kleine Steigung E_p.

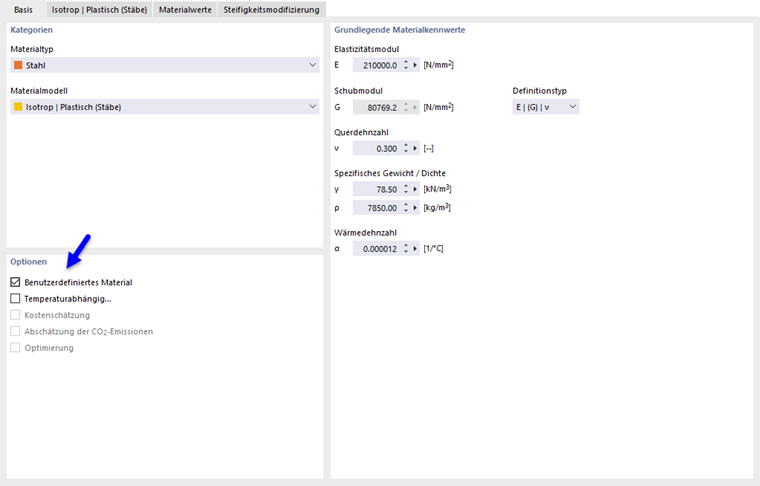
Wenn Sie die Werte für Streckgrenze und Elastizitätsmodul ändern möchten, aktivieren Sie das Kontrollkästchen "Benutzerdefiniertes Material" im Haupt-Reiter.

Benutzerdefiniertes Material aktivieren

Für eine bilineare Definition können Sie auch einen Wert für E_p eingeben.

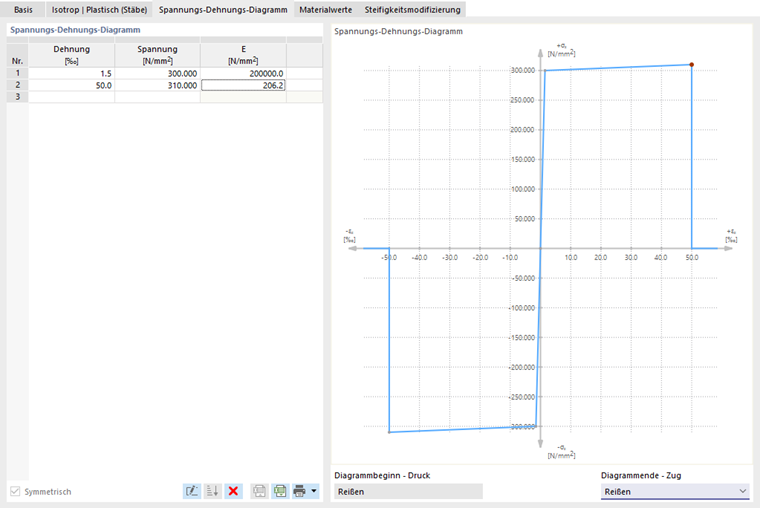
Komplexere Beziehungen zwischen Spannung und Dehnung können mittels des "Spannungs-Dehnungs-Diagramms" definiert werden. Wenn Sie diese Option auswählen, wird der Reiter "Spannungs-Dehnungs-Diagramm" angezeigt.

Benutzerdefiniertes Spannungs-Dehnungs-Diagramm eingeben

Definieren Sie einen Punkt für die Spannungs-Dehnungs-Beziehung in jeder Tabellenzeile. Sie können auswählen, wie das Diagramm nach dem letzten Definitionspunkt im "Diagramm-Ende"-Listenfeld unterhalb des Diagramms fortgesetzt wird:

Verlauf nach dem letzten Definitionspunkt

Im Fall von "Rissbildung" springt die Spannung nach dem letzten Definitionspunkt auf null zurück. "Fließen" bedeutet, dass die Spannung konstant bleibt, wenn die Dehnung zunimmt. "Kontinuierlich" bedeutet, dass das Diagramm mit der Steigung des letzten Abschnitts weitergeht.

Info

In diesem Materialmodell bezieht sich das Spannungs-Dehnungs-Diagramm auf die Längsspannung σ_x. Unterschiedliche Streckgrenzen für Zug und Druck können mit diesem Materialmodell nicht berücksichtigt werden.

Isotrop Plastisch | Flächen/Volumen

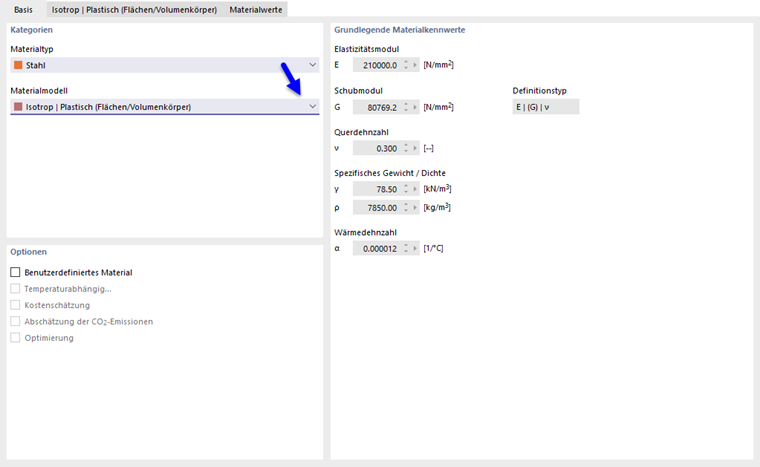
Beim Auswählen des Eintrags "Isotrop | Plastisch (Flächen/Volumen)" im Dropdown-Menü "Materialmodell" wird der Reiter zum Eingeben nichtlinearer Materialparameter aktiviert.

Plastisches Materialmodell auswählen

Zunächst wählen Sie die "Spannungsbruchhypothese" aus. Folgende Hypothesen stehen zur Auswahl:

von Mises (von Mises Fließkriterium)
Tresca (Tresca Fließkriterium)
Drucker-Prager
Mohr-Coulomb

Spannungsversagenshypothese festlegen

Bei der Auswahl von "von Mises" wird folgende Spannung im Spannungs-Dehnungs-Diagramm verwendet:

Flächen:

σ_{v} = \sqrt{σ_{x}^{2} + σ_{y}^{2} - σ_{x} σ_{y} + 3 (τ_{xy}^{2})}

Vergleichsspannung aus Grundspannungen nach von Mises

Volumen:

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Vergleichsspannung σ_v,Mises aus Grundspannungen

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Vergleichsspannung σ_v,Mises aus Hauptspannungen

Nach der "Tresca"-Hypothese wird folgende Spannung verwendet:

Flächen:

σ_{v} = \sqrt{{(σ_{x} - σ_{y})}^{2} + 4 {τ_{xy}}^{2}}

Vergleichsspannung nach Tresca

Volumen:

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Vergleichsspannung σ_v,Tresca

Nach der "Drucker-Prager"-Hypothese wird folgende Spannung für Flächen und Volumen verwendet:

σ_{v} = \frac{m - 1}{2} (σ_{1} + σ_{2} + σ_{3}) + \frac{m + 1}{2} \sqrt{\frac{1}{2} [{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}]}

m = \frac{σ_{c}}{σ_{t}}

σ_c	Grenzspannung für Druck
σ_t	Grenzspannung für Zug

Fließkriterium nach Drucker-Prager

Nach der "Mohr-Coulomb"-Hypothese wird folgende Spannung für Flächen und Volumen verwendet:

σ_{v} = \frac{m + 1}{2} \max \{|σ_{1} - σ_{2}| + K (σ_{1} + σ_{2}), |σ_{2} - σ_{3}| + K (σ_{2} + σ_{3}), |σ_{3} - σ_{1}| + K (σ_{3} + σ_{1})\}

K = \frac{m - 1}{m + 1}

m = \frac{σ_{c}}{σ_{t}}

Mohr–Coulomb

Isotrop Nichtlinear Elastisch | Stäbe

Die Funktionalität entspricht weitgehend der des isotropen plastischen (Stäbe) Materialmodells. Der Unterschied besteht darin, dass nach der Entlastung keine plastische Dehnung bleibt.

Isotrop Nichtlinear Elastisch | Flächen/Volumen

Die Funktionalität entspricht weitgehend der des isotropen plastischen (Flächen/Volumen) Materialmodells. Der Unterschied besteht darin, dass nach der Entlastung keine plastische Dehnung bleibt.

Isotrop Beschädigung | Flächen/Volumen

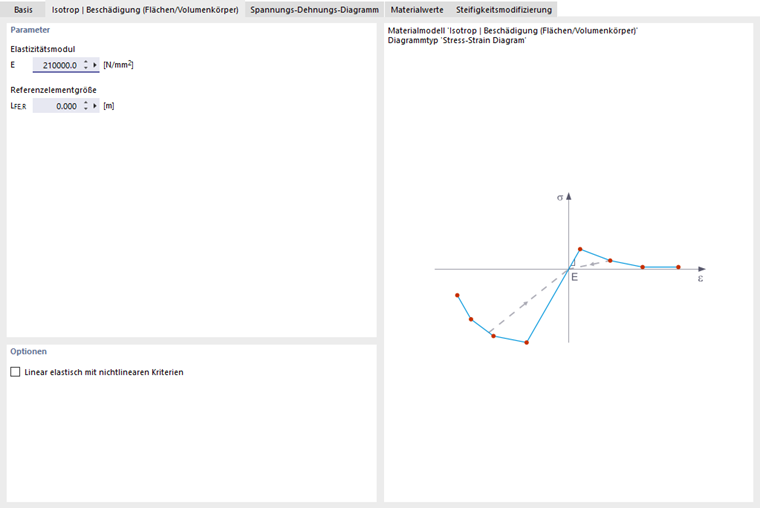
Im Gegensatz zu anderen Materialmodellen ist das Spannungs-Dehnungs-Diagramm für dieses Materialmodell nicht antimetric zum Ursprung. So kann mit diesem Materialmodell beispielsweise das Verhalten von stahlfaserverstärktem Beton dargestellt werden. Detaillierte Informationen zur Modellierung von stahlfaserverstärktem Beton finden Sie im technischen Artikel über die Bestimmung der Materialeigenschaften von stahlfaserverstärktem Beton.

Materialmodell 'Isotrop | Beschädigung'

In diesem Materialmodell wird die isotrope Steifigkeit mit einem skalaren Schaden-Parameter reduziert. Dieser Schaden-Parameter wird aus dem Spannungsverlauf bestimmt, der im Diagramm definiert ist. Dabei wird die Richtung der Hauptspannungen nicht berücksichtigt; vielmehr erfolgt der Schaden in Richtung der Äquivalentdehnung, welche auch die dritte, zur Ebene senkrechte Richtung umfasst. Der Zug- und Druckbereich des Spannungstensors wird separat behandelt. Verschiedene Schaden-Parameter gelten in jedem Fall.

Die "Referenzelementgröße" steuert, wie die Dehnung im Rissbereich auf die Länge des Elements skaliert wird. Mit dem Standardwert auf null wird keine Skalierung durchgeführt. So wird das Materialverhalten des stahlfaserverstärkten Betons realistisch modelliert.

Weitere Informationen zum theoretischen Hintergrund des "Isotrop Beschädigung" Materialmodells finden Sie im technischen Artikel über das nichtlineare Materialmodell Schaden.

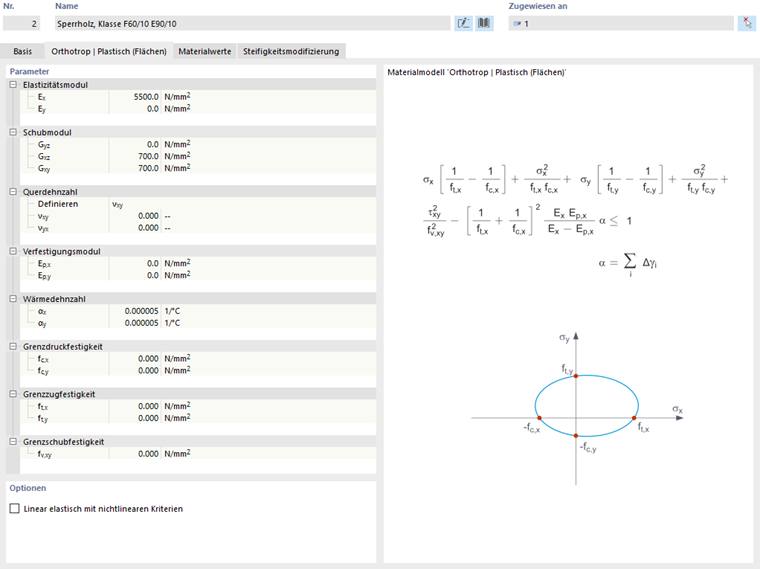
Orthotrop Plastisch | Flächen/Volumen

Das Materialmodell nach "Tsai-Wu" vereint plastische mit orthotropen Eigenschaften. Dies ermöglicht eine spezielle Modellierung von Materialien mit anisotropen Eigenschaften, wie faserverstärkte Kunststoffe oder Holz.

Wenn das Material plastifiziert ist, bleiben die Spannungen konstant. Die Umverteilung erfolgt nach den in den einzelnen Richtungen vorhandenen Steifigkeiten.

Materialmodell 'Orthotrop | Plastisch (Flächen)'

Materialmodell 'Orthotrop | Plastisch (Volumenkörper)'

Der elastische Bereich entspricht dem orthotropen Materialmodell. Die folgende Fließbedingung nach Tsai-Wu gilt für die plastische Zone:

Flächen (2D):

σ_{x} [\frac{1}{f_{t, x}} - \frac{1}{f_{c, x}}] + \frac{{σ_{x}}^{2}}{f_{t, x} f_{c, x}} +

σ_{y} [\frac{1}{f_{t, y}} - \frac{1}{f_{c, y}}] + \frac{{σ_{y}}^{2}}{f_{t, y} f_{c, y}} +

\frac{{τ_{xy}}^{2}}{{f_{v, xy}}^{2}} - {[\frac{1}{f_{t, x}} + \frac{1}{f_{c, x}}]}^{2} \frac{E_{x} E_{p, x}}{E_{x} - E_{p, x}} α \leq 1

α = \sum_{i} ∆ γ_{i}

Tsai-Wu, ebener Spannungszustand

Volumen (3D):

σ_{x} [\frac{1}{f_{t, x}} - \frac{1}{f_{c, x}}] + \frac{{σ_{x}}^{2}}{f_{t, x} f_{c, x}} +

σ_{y} [\frac{1}{f_{t, y}} - \frac{1}{f_{c, y}}] + \frac{{σ_{y}}^{2}}{f_{t, y} f_{c, y}} +

σ_{z} [\frac{1}{f_{t, z}} - \frac{1}{f_{c, z}}] + \frac{{σ_{z}}^{2}}{f_{t, z} f_{c, z}} +

\frac{{τ_{yz}}^{2}}{{f_{v, yz}}^{2}} + \frac{{τ_{xz}}^{2}}{{f_{v, xz}}^{2}} + \frac{{τ_{xy}}^{2}}{{f_{v, xy}}^{2}} -

{[\frac{1}{f_{t, x}} + \frac{1}{f_{c, x}}]}^{2} \frac{E_{x} E_{p, x}}{E_{x} - E_{p, x}} α \leq 1

α = \sum_{i} ∆ γ_{i}

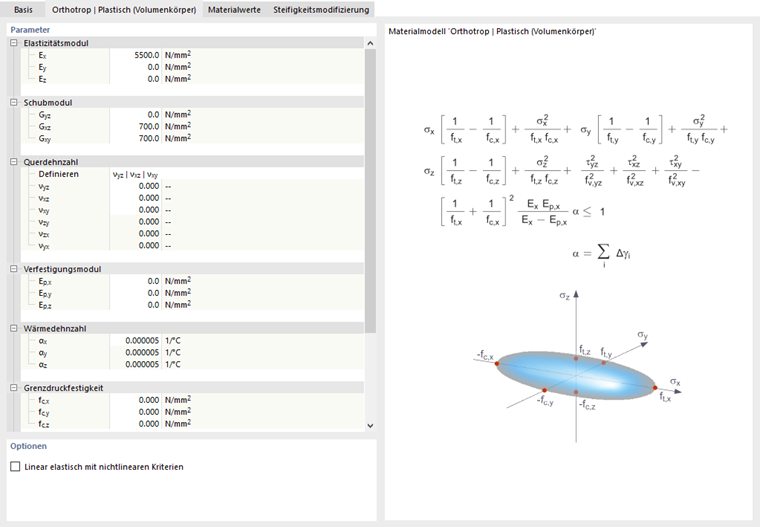
Tsai-Wu, räumlicher Spannungszustand

Alle Festigkeiten müssen positiv definiert werden.

Sie können sich das Spannungskriterium als eine elliptische Fläche in einem sechsdimensionalen Spannungsraum vorstellen. Wenn eine der drei Spannungs-Komponenten als konstanter Wert angewendet wird, kann die Fläche auf einen dreidimensionalen Spannungsraum projiziert werden.

Wenn der Wert für f_y(σ) gemäß der Tsai-Wu-Gleichung, Ebener Spannungszustand, kleiner als 1 ist, befinden sich die Spannungen im elastischen Bereich. Die plastische Zone ist erreicht, sobald f_y(σ) = 1. Werte größer als 1 sind nicht zulässig. Das Modellverhalten ist ideal-plastisch, das heißt es erfolgt keine Versteifung.

Übergeordnetes Kapitel

Nichtlinearität