Instrukcje online Walidacja oprogramowania

88x

004088

2023-09-28

Wybór ręczny

Nieliniowość materiału

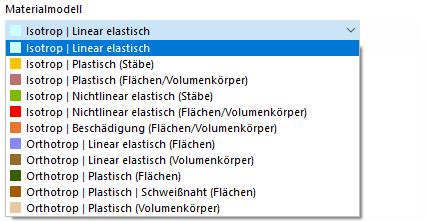
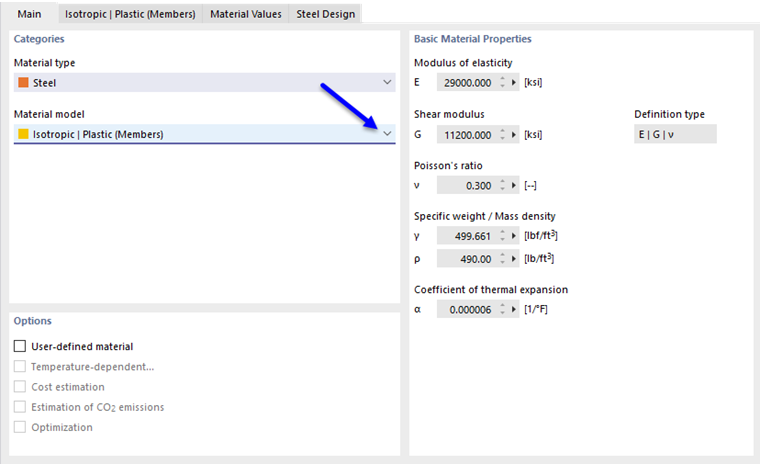
Jeżeli w sekcji Dane podstawowe modelu aktywowano rozszerzenie Nieliniowa analiza zachowania materiału (wymagana licencja), na liście modeli materiałowych oprócz opcji 'Izotropowy dostępne są dalsze opcje do wyboru. | Liniowo sprężysty' i 'Ortotropowy | liniowo-sprężysty' dostępne są także inne opcje.

Modele materiałowe dla 'Nieliniowego zachowania materiału' Rozszerzenie

W przypadku korzystania z nieliniowych modeli materiałowych w programie RFEM zawsze przeprowadzane są obliczenia iteracyjne. W zależności od modelu materiałowego definiowana jest inna zależność między naprężeniami a odkształceniami.

Sztywność elementów skończonych jest dostosowywana w trakcie iteracji, aż do osiągnięcia zależności naprężenie-odkształcenie. Dopasowanie jest zawsze przeprowadzane dla całej powierzchni lub elementu bryłowego. Z tego względu podczas oceny naprężeń zaleca się zawsze stosować typ uśredniania Stałe w elementach siatki.

Uśrednianie wyników

Niektóre modele materiałowe w programie RFEM są oznaczone jako 'plastyczne', inne jako 'nieliniowo-sprężyste'.

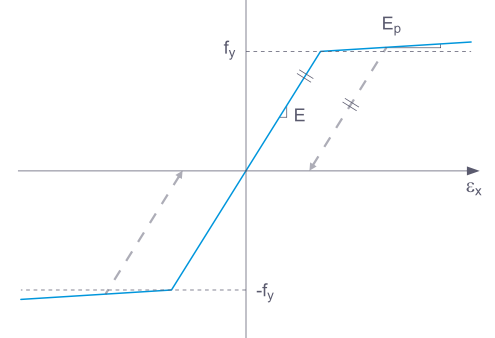
Jeżeli element konstrukcyjny z materiałem nieliniowo-sprężystym zostanie odciążony, odkształcenie powraca wzdłuż tej samej ścieżki. Po całkowitym odciążeniu odkształcenie zanika.

Wykres naprężenie-odkształcenie, nieliniowy wykres sprężysty

W przypadku elementu konstrukcyjnego z plastycznym modelem materiałowym odkształcenie występuje także po całkowitym odciążeniu.

Wykres naprężenie-odkształcenie, tworzywo sztuczne

Podstawowe informacje na temat nieliniowych modeli materiałowych można znaleźć w artykule technicznym dotyczącym Prawa plastyczności w izotropowej nieliniowej konstrukcji sprężystej model materiałowy.

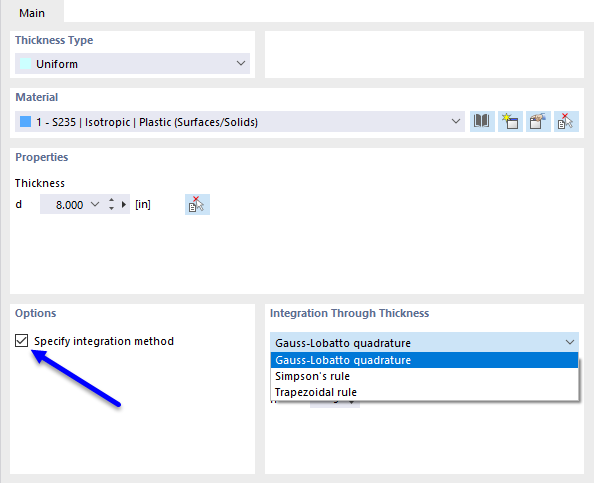
Siły wewnętrzne w płytach z materiałem nieliniowym wynikają z całkowania numerycznego naprężeń po grubości płyty. W celu zdefiniowania metody całkowania dla grubości w oknie dialogowym 'Edytować grubość' należy wybrać opcję Określić metodę całkowania. Dostępne są następujące metody całkowania:

kwadratura Gaussa-Lobatto
metoda Simpsona
metoda trapezów

Zdefiniuj metodę całkowania dla grubości powierzchni

Ponadto można zadać 'Liczbę punktów całkowania' na grubości płyty w zakresie od 3 do 99.

Informacje

Teoretyczne wyjaśnienie poszczególnych metod integracji można znaleźć na multilayer-surface-laminate-clt/003939 Instrukcja online Powierzchnie wielowarstwowe .

Izotropowy plastyczny (pręty)

W przypadku wybrania z listy rozwijanej "Model materiałowy" opcji Izotropowy | plastyczny (pręty) aktywowana zostaje zakładka do wprowadzania nieliniowych parametrów materiału.

Aktywacja nieliniowego modelu materiałowego

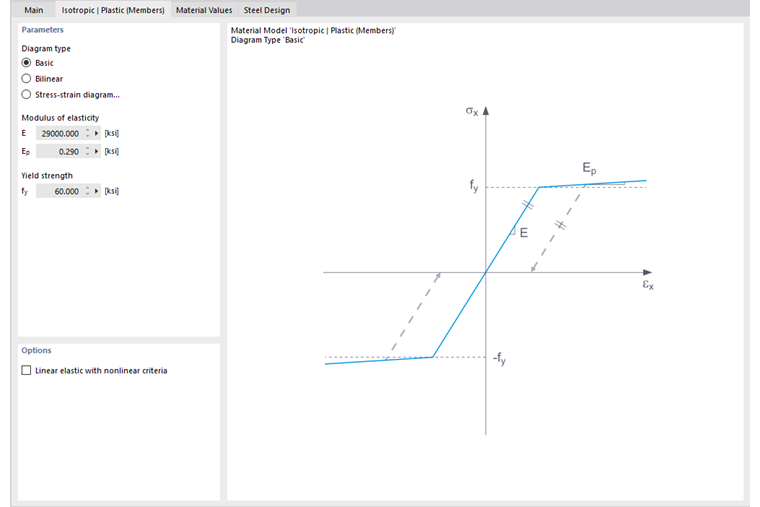
Zdefiniuj nieliniowe parametry materiałowe

W tej zakładce należy zdefiniować wykres naprężenie-odkształcenie. Dostępne są następujące opcje:

Informacje ogólne
Dwuliniowy
Wykres naprężenie-odkształcenie

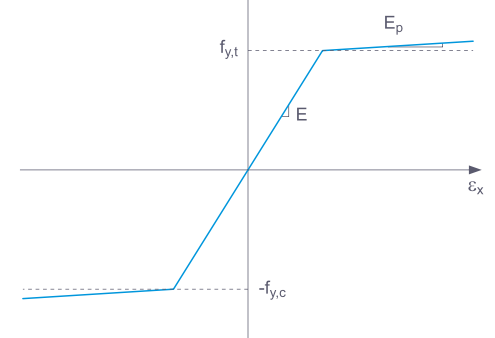
W przypadku wybrania opcji Podstawowe ' program RFEM stosuje bilinearny model materiałowy. Jako moduł sprężystości E i granica plastyczności f_y wykorzystywane są wartości z bazy danych materiałów. Gałąź wykresu ze względów numerycznych nie jest dokładnie pozioma, lecz ma niewielkie nachylenie E_p.

Aby zmienić wartości dla granicy plastyczności i modułu sprężystości, należy aktywować w zakładce 'Materiał główny' pole wyboru 'Materiał zdefiniowany przez użytkownika'.

Aktywuj materiał zdefiniowany przez użytkownika

W przypadku definicji dwuliniowej można również wprowadzić wartość parametru E_p.

Bardziej złożone zależności między naprężeniem a odkształceniem można zdefiniować za pomocą "Wykresu naprężenie-odkształcenie". Po wybraniu tej opcji wyświetlana jest zakładka 'Wykres naprężenie-odkształcenie'.

Wprowadź zdefiniowany przez użytkownika wykres naprężenie-odkształcenie

W każdym wierszu tabeli należy zdefiniować punkt dla stosunku naprężenie-odkształcenie. Sposób, w jaki wykres będzie przebiegał za ostatnim punktem definicji, można wybrać z listy 'Koniec wykresu' pod wykresem:

Rozkład za ostatnim punktem definicji

W przypadku 'Przerwania', naprężenie po ostatnim punkcie definicji powraca do zera. 'Uplastycznienie' oznacza, że naprężenie pozostaje stałe wraz ze wzrostem odkształcenia. 'Ciągły' oznacza, że wykres jest kontynuowany z nachyleniem z ostatniego przekroju.

Informacje

W tym modelu materiałowym wykres naprężenie-odkształcenie odnosi się do naprężenia podłużnego σ_x. W tym modelu materiałowym nie można uwzględnić różnych granic plastyczności dla rozciągania i ściskania.

Izotropowy plastyczny (powierzchnie/bryły)

W przypadku wybrania opcji „Izotropowy | Plastyczny (powierzchnie/bryły)" z listy rozwijanej 'Model materiałowy', aktywuje się zakładka do wprowadzania nieliniowych parametrów materiału.

Wybierz model z tworzywa sztucznego

Wählen Sie zunächst die 'Spannungsversagenshypothese' aus. Prosimy o podanie hipotezy:

Najpierw należy wybrać 'Naprężeniową hipotezę zniszczenia'. Do wyboru są następujące hipotezy:

von Mises (kryterium uplastycznienia von Mises'a)
Tresca (kryterium uplastycznienia Tresca)
Drucker-Prager
Mohr-Coulomb

Zdefiniuj hipotezę uszkodzenia naprężeniowego

W przypadku wybrania opcji „von Mises” na wykresie naprężenie-odkształcenie stosowane jest następujące naprężenie:

Powierzchnie:

σ_{v} = \sqrt{σ_{x}^{2} + σ_{y}^{2} - σ_{x} σ_{y} + 3 (τ_{xy}^{2})}

Naprężenia równoważne z naprężeń podstawowych według von Misesa

Bryły:

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{xy}^{2} + τ_{xz}^{2} + τ_{yz}^{2})}

Naprężenie równoważne σ_v,Mises z naprężeń podstawowych

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Naprężenie równoważne σ_{v, Mises} z naprężeń głównych

Zgodnie z hipotezą "Tresca" stosowane jest następujące naprężenie:

Powierzchnie:

σ_{v} = \sqrt{{(σ_{x} - σ_{y})}^{2} + 4 {τ_{xy}}^{2}}

Naprężenie równoważne według Tresca

Bryły:

σ_{v, Tresca} = max (|σ_{1} - σ_{2}|; |σ_{2} - σ_{3}|; |σ_{3} - σ_{1}|)

Naprężenie równoważne σ_{v, Tresca}

Zgodnie z hipotezą "Druckera-Pragera" dla powierzchni i brył stosuje się następujące naprężenie:

σ_{v} = \frac{m - 1}{2} (σ_{1} + σ_{2} + σ_{3}) + \frac{m + 1}{2} \sqrt{\frac{1}{2} [{(σ_{1} - σ_{2})}^{2} + {(σ_{2} - σ_{3})}^{2} + {(σ_{3} - σ_{1})}^{2}]}

m = \frac{σ_{c}}{σ_{t}}

σ_C	Naprężenie graniczne przy ściskaniu
σ_t	Naprężenie graniczne dla rozciągania

Kryterium wydajności według Druckera-Pragera

Zgodnie z hipotezą "Mohra-Coulomba" dla powierzchni i brył stosuje się następujące naprężenie:

σ_{v} = \frac{m + 1}{2} \max \{|σ_{1} - σ_{2}| + K (σ_{1} + σ_{2}), |σ_{2} - σ_{3}| + K (σ_{2} + σ_{3}), |σ_{3} - σ_{1}| + K (σ_{3} + σ_{1})\}

K = \frac{m - 1}{m + 1}

m = \frac{σ_{c}}{σ_{t}}

Mohr-Coulomb

Izotropowy nieliniowy sprężysty (pręty)

Funkcjonalność w dużej mierze odpowiada funkcjonalności izotropowego plastycznego modelu materiałowego (pręty). Różnica polega na tym, że po odciążeniu znika odkształcenie plastyczne.

Izotropowy nieliniowy sprężysty (powierzchnie/bryły)

Funkcjonalność w dużej mierze odpowiada funkcjonalności izotropowego plastycznego modelu materiałowego (powierzchnie/bryły). Różnica polega na tym, że po odciążeniu znika odkształcenie plastyczne.

Uszkodzenie izotropowe (powierzchnie/bryły)

W przeciwieństwie do innych modeli materiałowych, wykres naprężenie-odkształcenie dla tego modelu materiałowego nie jest antymetryczny względem początku. W ten sposób za pomocą tego modelu materiałowego można wyświetlić, na przykład, zachowanie betonu zbrojonego włóknami stalowymi. Szczegółowe informacje na temat modelowania betonu zbrojonego włóknami stalowymi można znaleźć w artykule technicznym na temat Określanie właściwości materiałowych włókien stalowych żelbet.

Model materiałowy „Izotropowy | Uszkodzenia"

W tym modelu materiału sztywność izotropowa jest redukowana za pomocą skalarnego parametru uszkodzenia. Ten parametr uszkodzenia wyznaczany jest z krzywej naprężeń określonej na wykresie. Nie uwzględnia się kierunku naprężeń głównych. Zamiast tego uszkodzenie występuje w kierunku odkształcenia zastępczego, które obejmuje również trzeci kierunek prostopadły do płaszczyzny. Obszary rozciągania i ściskania tensora naprężeń są traktowane oddzielnie. W każdym przypadku obowiązują inne parametry uszkodzenia.

"Wielkość elementu odniesienia" określa, w jaki sposób odkształcenie w obszarze rys jest skalowane do długości elementu. Przy domyślnej wartości zero skalowanie nie jest wykonywane. Pozwala to na realistyczne modelowanie zachowania materiałowego betonu zbrojonego włóknami stalowymi.

Więcej informacji na temat podstaw teoretycznych modelu materiałowego 'uszkodzenia izotropowego' można znaleźć w artykule technicznym opisującym [https://www.dlubal.com/pl/support-and-learning/support/knowledge-base/001461 Uszkodzenie modelu nieliniowego materiału.

Ortotropowy plastyczny (powierzchnie)/Ortotropowy plastyczny (bryły)

Model materiałowy według "Tsai-Wu" łączy właściwości plastyczne i ortotropowe. Pozwala to na specjalne modelowanie materiałów o właściwościach anizotropowych, takich jak tworzywa sztuczne wzmocnione włóknami lub drewno.

Podczas uplastycznienia materiału naprężenia pozostają stałe. Zachodzi redystrybucja w zależności od sztywności występującej w poszczególnych kierunkach.

BILD

Obszar sprężysty odpowiada modelowi materiałowemu Ortotropowy. W strefie plastycznej ma zastosowanie następujący warunek uplastycznienia według Tsai-Wu:

Powierzchnie (2D):

FORMEL

Bryły (3D):

FORMEL

Wszystkie wytrzymałości należy zdefiniować jako dodatnie.

Warunek plastyczności można wyobrazić sobie jako powierzchnię w kształcie elipsy w sześciowymiarowej przestrzeni naprężeń. Jeżeli jedna z trzech składowych naprężenia zostanie przyłożona jako stała wartość, powierzchnię tę można rzutować na trójwymiarową przestrzeń naprężeń.

Jeżeli wartość f_y (σ) według równania Tsai-Wu, płaski warunek naprężenia, jest mniejsza niż 1, naprężenia znajdują się w strefie sprężystej. Strefa plastyczna zostaje osiągnięta, gdy tylko_y (σ) = 1. Wartości większe niż 1 nie są dozwolone. Zachowanie modelu jest idealnie plastyczne, co oznacza, że nie występuje usztywnienie.

Rozdział nadrzędny

Nieliniowość