77x

004088

28.9.2023

Vybrat manuál

Nelinearita materiálu

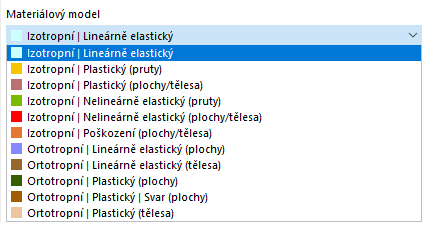
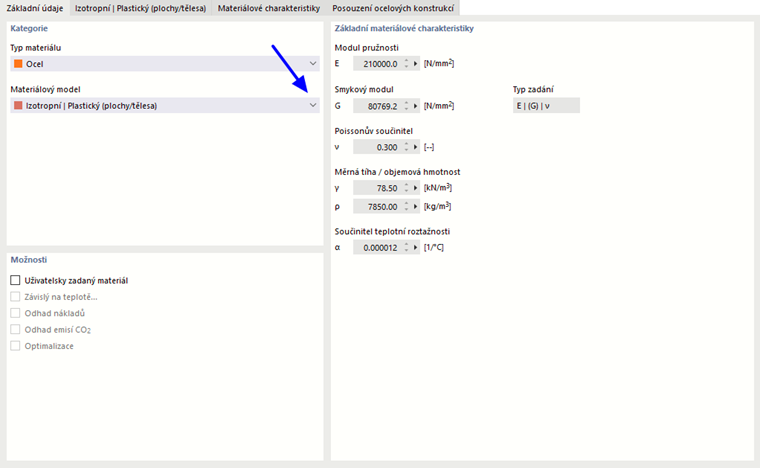
Pokud je v Základních údajích modelu aktivován addon Nelineární analýza chování materiálu (nutná licence), jsou v seznamu materiálových modelů kromě možnosti 'Izotropní k dispozici další možnosti pro výběr | Lineárně elastický' a 'ortotropní | Lineárně elastický' v seznamu materiálových modelů k dispozici další možnosti.

Materiálové modely pro addon ' Nelineární chování materiálu '

Pokud v programu RFEM používáte nelineární materiálové modely, provádí se vždy iterační výpočet. V závislosti na materiálovém modelu je definována patřičná závislost napětí a přetvoření.

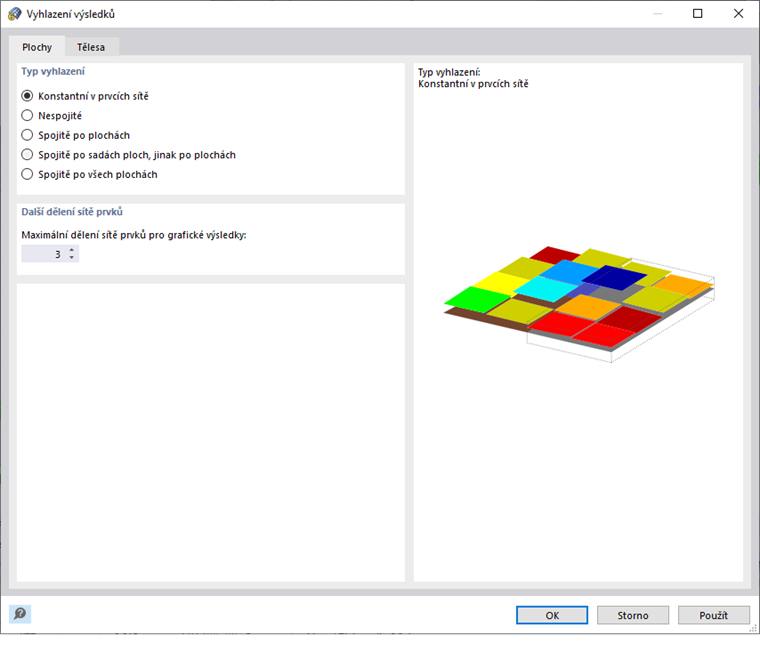
Tuhost konečných prvků se v průběhu iterací znovu a znovu upravuje, aby byl dodržen vztah mezi napětím a přetvořením. Úprava se provádí vždy pro celou plochu nebo těleso. Proto doporučujeme při vyhodnocování napětí vždy používat typ vyhlazení Konstantní na prvcích sítě.

Vyhlazení výsledků

Některé materiálové modely jsou v programu RFEM označeny jako 'plastické', jiné jako 'nelineárně elastické'.

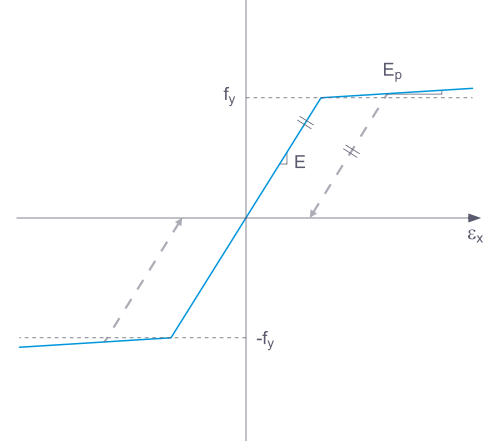
Pokud se konstrukční prvek z nelineárně elastického materiálu opět odlehčí, vrátí se přetvoření stejnou cestou zpět. Při úplném odlehčení nezůstává žádné přetvoření.

Pracovní diagram, nelineárně elastický

Při odlehčování konstrukčního prvku s plastickým materiálovým modelem zůstává po úplném odlehčení zbytkové přetvoření.

Pracovní diagram, plastický

Základní informace o nelineárních materiálových modelech najdete v odborném článku, který popisuje Podmínky plasticity v izotropním nelineárním elastiku materiálový model.

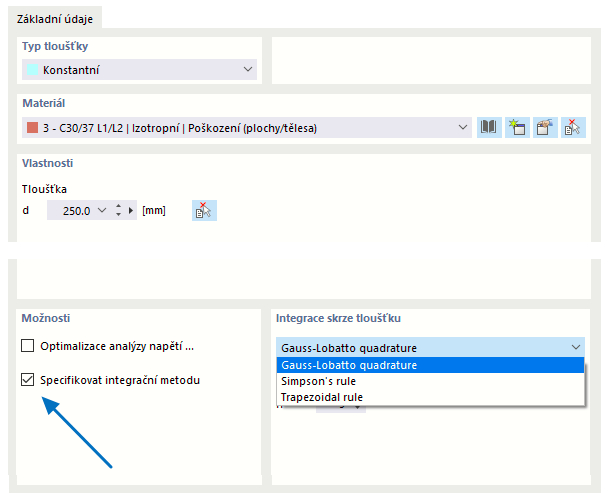
Vnitřní síly v deskách z nelineárního materiálu vyplývají z numerické integrace napětí přes tloušťku d desky. Chcete-li zadat metodu integrace pro tloušťku, vyberte v dialogu 'Upravit tloušťku' možnost Zadat metodu integrace. K dispozici jsou následující metody integrace:

Gaussova-Lobattova kvadratura
Simpsonovo pravidlo
Lichoběžníkové pravidlo

Zadat integrační metodu pro tloušťku plochy

Dále lze zadat 'počet integračních bodů' od 3 do 99 podle tloušťky plechu.

Informace

Teoretické vysvětlení jednotlivých metod integrace lze najít na multivrstve-plochy-laminat-clt/003939 Vícevrstvé plochy online manuál.

Izotropní plastický (pruty)

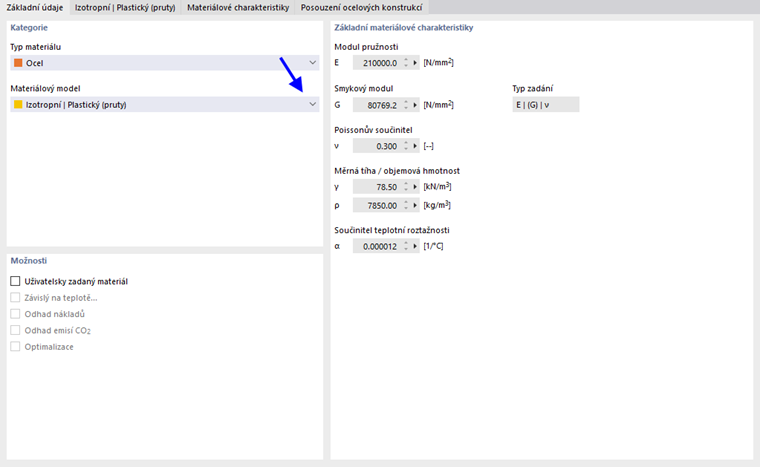
Při výběru možnosti Izotropní | Plastický (pruty), vytvoří se záložka pro zadání nelineárních materiálových parametrů.

Aktivujte nelineární materiálový model

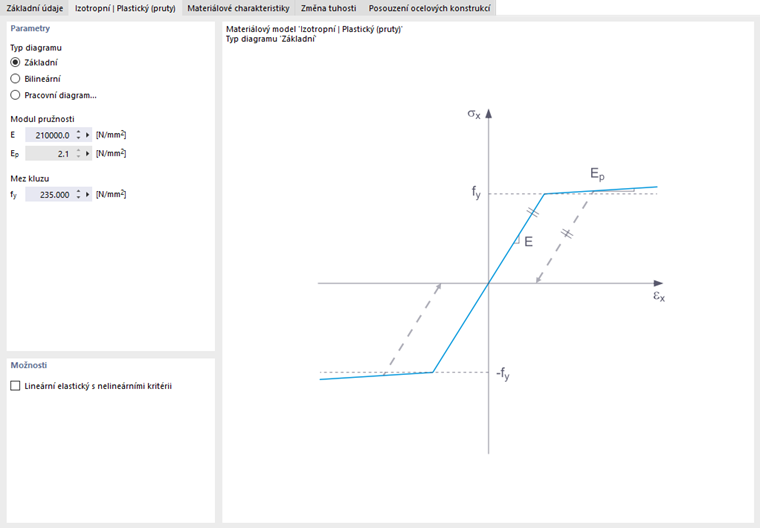
Definujte nelineární parametry materiálu

V této záložce zadejte závislost napětí-přetvoření. K dispozici jsou následující možnosti:

Basic
Bilineární
Pracovní diagram

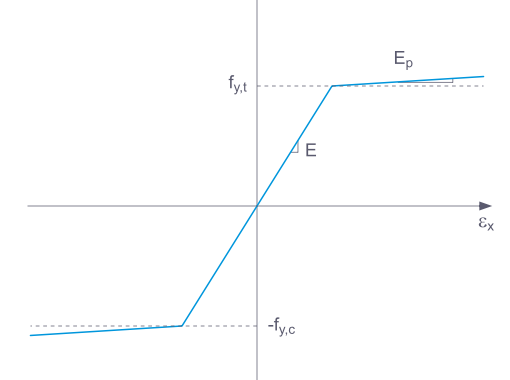
Pokud vybereme Základní ', použije RFEM bilineární materiálový model. Pro modul pružnosti E a mez kluzu f_y se použijí hodnoty z databáze materiálů. Z numerických důvodů není větev grafu přesně vodorovná, ale má malý sklon E_p.

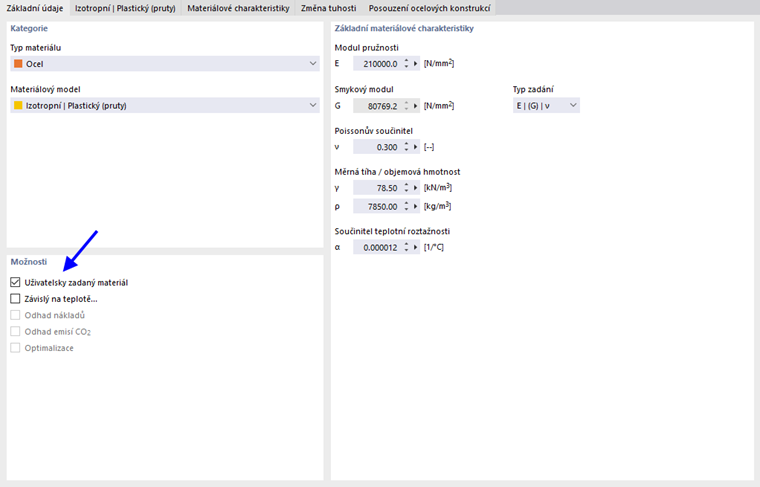
Pokud chcete změnit hodnoty meze kluzu a modulu pružnosti, zaškrtněte políčko "Uživatelsky zadaný materiál" v záložce 'Základní údaje'.

Aktivovat uživatelsky definovaný materiál

Pro bilineární zadání je možné zadat také hodnotu pro E_p.

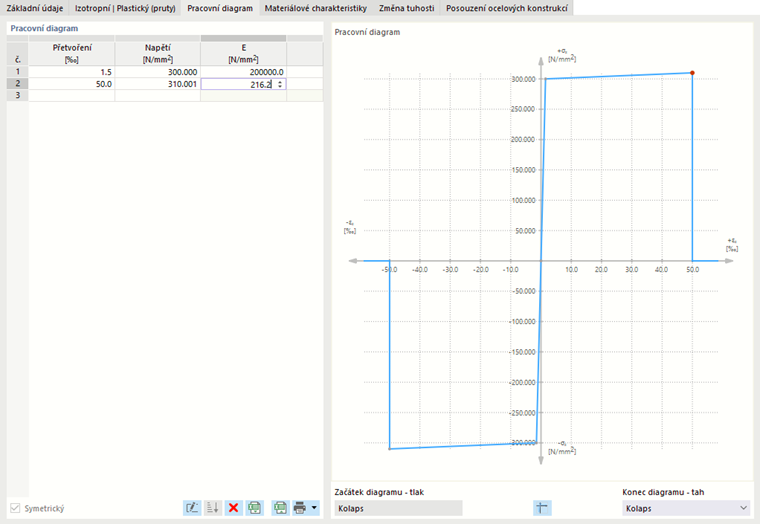
Složitější vztahy mezi napětím a přetvořením lze definovat pomocí "diagramu napětí-přetvoření". Pokud zaškrtnete tuto možnost, zobrazí se záložka 'Pracovní diagram'.

Zadejte uživatelsky definovaný pracovní diagram

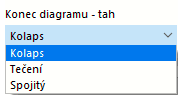
V každém řádku definujte bod pro závislost napětí-přetvoření. V seznamu 'Konec diagramu' pod diagramem můžete vybrat, jak má diagram pokračovat za posledním definičním bodem:

Průběh za posledním definičním bodem

V případě možnosti 'Kolaps' spadne napětí za posledním definičním bodem zpět na nulu. 'Tečení' znamená, že napětí zůstane konstantní s rostoucím přetvořením. 'Spojitý' znamená, že křivka pokračuje se sklonem stejným jako mezi posledními body.

Informace

V tomto materiálovém modelu se pracovní diagram vztahuje k podélnému napětí σ_x. Rozdílné meze kluzu pro tah a tlak nelze u tohoto materiálového modelu zohlednit.

Izotropní plastický (plochy/tělesa)

Při výběru možnosti "Izotropní | Plastický (plochy/tělesa)“ v rozbalovacím seznamu 'Materiálový model', je aktivována záložka pro zadání nelineárních materiálových parametrů.

Výběr plastického materiálového modelu

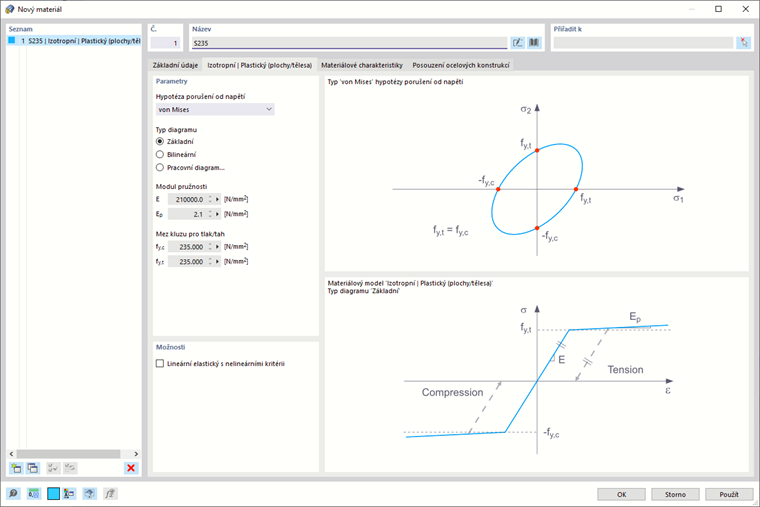
Wählen Sie zunächst die 'Spannungsversagenshypothese' aus. Zur Auswahl stehen diese Hypothesen:

Nejprve vyberte 'Hypotézu porušení od napětí' (pevnostní hypotézu). Můžete si vybrat z následujících hypotéz:

von Mises (energetická hypotéza)
Tresca (hypotéza max. smykového napětí)
Drucker-Prager
Mohr-Coulomb

Definujte hypotézu selhání napětí

Při volbě „von Mises“ se v pracovním diagramu použije následující napětí:

Plochy:

σ_{v} = \sqrt{σ_{x}^{2} + σ_{y}^{2} - σ_{x} σ_{y} + 3 (τ_{x y}^{2})}

Srovnávací napětí ze základních napětí podle von Misese

Tělesa:

σ_{v, Mises} = \sqrt{σ_{x}^{2} + σ_{y}^{2} + σ_{z}^{2} - σ_{x} σ_{y} - σ_{x} σ_{z} - σ_{y} σ_{z} + 3 (τ_{x y}^{2} + τ_{x z}^{2} + τ_{y z}^{2})}

Srovnávací napětí σ_{v, Mises} ze základních napětí

σ_{v, Mises} = \sqrt{\frac{1}{2} [(σ_{1} - σ_{2})^{2} + (σ_{1} - σ_{3})^{2} + (σ_{2} - σ_{3})^{2}]}

Srovnávací napětí σ_{v, Mises} z hlavních napětí

Podle „Trescovy“ hypotézy se použije následující napětí:

Plochy:

σ_{v} = \sqrt{(^{σ_{x} - σ_{y}) 2} + 4 {τ_{x y}}^{2}}

Srovnávací napětí podle Trescy

Tělesa:

σ_{v, Tresca} = max (|σ_{1} - σ_{2}); |σ_{2} - σ_{3}); |σ_{3} - σ_{1}))|||

Srovnávací napětí σ_{v, Tresca}

Podle „Drucker-Pragerovy“ hypotézy se pro plochy a tělesa používá následující napětí:

σ_{v} = \frac{m - 1}{2} (σ_{1} + σ_{2} + σ_{3}) + \frac{m + 1}{2} \sqrt{\frac{1}{2} [(^{σ_{1} - σ_{2}) 2} + (^{σ_{2} - σ_{3}) 2} + (^{σ_{3} - σ_{1}) 2})]}

m = \frac{σ_{c}}{σ_{t}}

σ_c	Mezní napětí v tlaku
σ_t	Mezní napětí v tahu

Výnosové kritérium podle Drucker-Prager

Podle „Mohr-Coulombovy“ hypotézy se pro plochy a tělesa používá následující napětí:

σ_{v} = \frac{m + 1}{2} m a x \{|σ_{1} - σ_{2}) + K (σ_{1} + σ_{2}), |σ_{2} - σ_{3}) + K (σ_{2} + σ_{3}), |σ_{3} - σ_{1}) + K (σ_{3} + σ_{1})|||)\}

K = \frac{m - 1}{m + 1}

m = \frac{σ_{c}}{σ_{t}}

Mohr - Coulomb

Izotropní nelineárně elastický (pruty)

Funkčnost do značné míry odpovídá izotropnímu plastickému (prutovému) materiálovému modelu. Na rozdíl od něj však po odlehčení napětí nedochází k žádné plastické deformaci.

Izotropní nelineárně elastický (plochy/tělesa)

Funkčnost do značné míry odpovídá izotropnímu plastickému materiálovému modelu (plochy/tělesa). Na rozdíl od něj však po odlehčení napětí nedochází k žádné plastické deformaci.

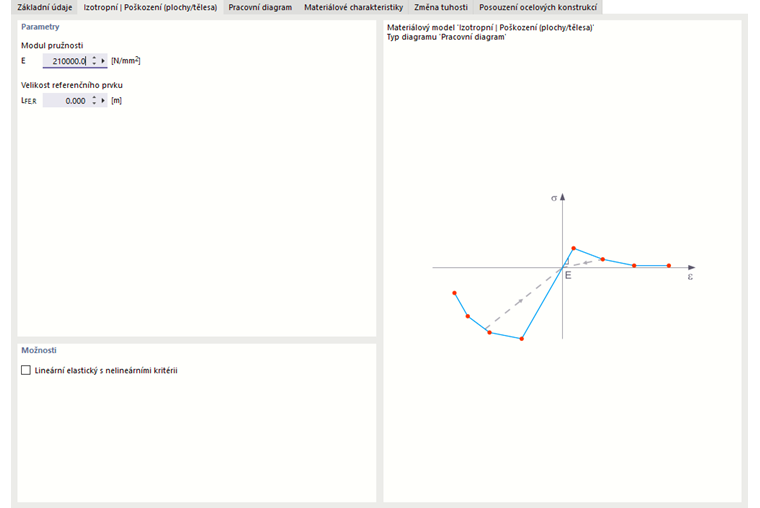
Izotropní Poškození (plochy/tělesa)

Na rozdíl od jiných materiálových modelů není pracovní diagram pro tento materiálový model antimetrický vzhledem k počátku. Tímto způsobem lze například modelovat chování drátkobetonu. Podrobné informace o modelování drátkobetonu najdete v odborném článku Stanovení materiálových vlastností drátkobetonu železobeton.

Materiálový model "Izotropní | Poškození "

U tohoto materiálového modelu je izotropní tuhost redukována skalárním parametrem poškození. Tento parametr poškození se stanoví na základě průběhu napětí, které je definováno v diagramu. V tomto případě se nezohledňuje směr hlavních napětí, ale dochází k poškození ve směru srovnávacího poměrného přetvoření, které zahrnuje také třetí směr kolmý na rovinu. Tahové a tlakové oblasti tenzoru napětí jsou řešeny odděleně. V každém případě platí různé parametry poškození.

Velikost "referenčního prvku" určuje, jak se má přetvoření v oblasti trhlin přizpůsobit délce prvku. Při přednastavené nulové hodnotě nedochází ke změně měřítka. Tímto způsobem se téměř realisticky modeluje materiálové chování drátkobetonu.

Další informace o teoretickém pozadí materiálového modelu 'Izotropní poškození' najdete v odborném článku [https://www.dlubal.com/cs/podpora-a-skoleni/podpora/databaze-znalosti/001461 Poškození nelineárního materiálového modelu.

Ortotropní plastický (plochy) / Ortotropní plastický (tělesa)

Materiálový model Tsai-Wu propojuje plastické a ortotropní vlastnosti. To umožňuje speciální modelování materiálů s anizotropními vlastnostmi, jako jsou plasty vyztužené vlákny nebo dřevo.

Při plastizaci materiálu zůstávají napětí konstantní. Dochází k jejich redistribuci v závislosti na tuhosti v jednotlivých směrech.

BILD

Pružná oblast odpovídá ortotropnímu materiálovému modelu. Pro plastickou oblast platí následující podmínka plasticity podle Tsai-Wu:

Plochy (2D):

FORMEL

Tělesa (3D):

FORMEL

Veškeré pevnosti je třeba zadat jako kladné hodnoty.

Podmínku plasticity si můžeme představit jako plochu ve tvaru elipsy v šestirozměrném prostoru napjatosti. Pokud se jedna z daných tří složek napětí uvažuje jako konstantní hodnota, lze plochu promítnout do trojrozměrného prostoru napjatosti.

Pokud je hodnota f_y (σ) podle rovnice Tsai-Wu, rovinná napjatost, menší než 1, jsou napětí v pružné oblasti. Plastické oblasti je dosaženo, jakmile f_y (σ) = 1. Hodnoty vyšší než 1 nejsou přípustné. Chování modelu je ideálně-plastické, to znamená, že nedochází k žádnému vyztužení.

Nadřazená kapitola

Nelinearita