描述
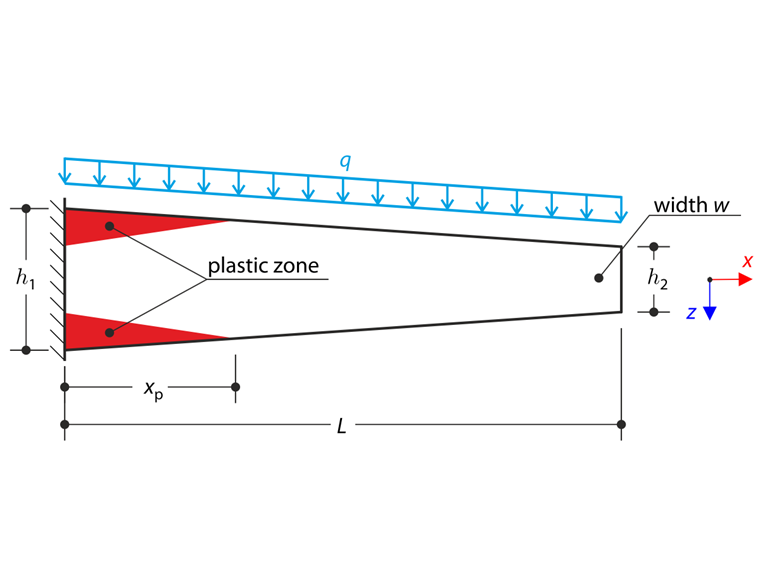
一根变截面悬臂梁在左端完全固定，并承受连续荷载 q。 在这个例子中考虑了小变形，并且忽略了自重。 该问题由以下一组参数描述。 确定最大挠度 uz,max 。
| 材料 | 弹塑性 | 弹性模量 | E | 210000,000 | MPa |
| 泊松比 | ν | 0,000 | - | ||
| 剪切模量 | G | 105000,000 | MPa | ||
| 屈服强度 | [F12]y | 40,000 | MPa | ||
| 几何形状 | 悬臂梁 | 周长 | l | 4,000 | m |
| 宽度 | w | 0.005 | m | ||
| 左侧高度 | h1 | 0,250 | m | ||
| 右侧高度 | h2 | 0.150 | m | ||
| 荷载 | 连续荷载 | q | 2300,000 | N/m | |
解析解
这是验证示例 17 的更复杂的变体。 在这种情况下考虑变截面悬臂梁。 连续荷载 q 导致板的弹塑性状态。 计算过程与验算例 17 类似。
02
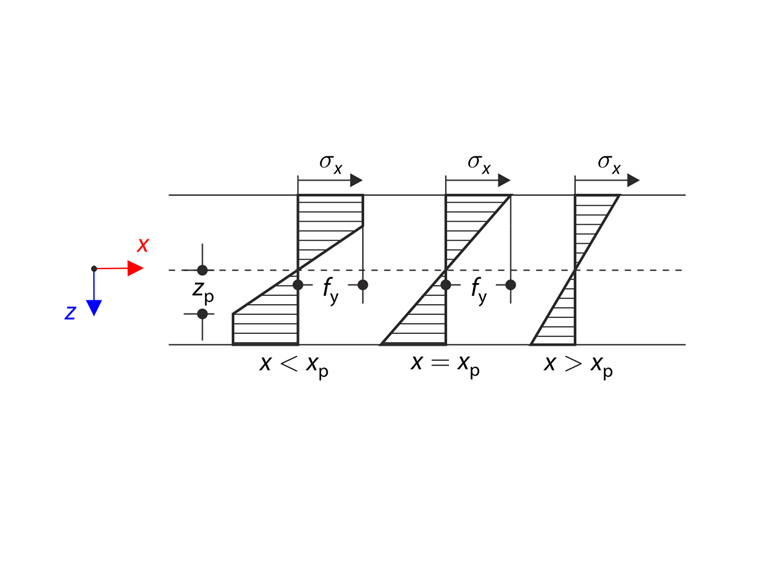
弯曲应力分布
弹塑性弯矩 Mep （内力）必须等于弯矩 M（外力）。 弹塑性区域中的曲率 κp就是由这个等式得出的。
使用 Mohr' 积分将结构的总挠度定义为弹塑性和弹性贡献的叠加。
RFEM 设置
- 在 RFEM 5.26 和 RFEM 6.02 中建模
- 单元尺寸 lFE =0.020 m 文件 0018.01-0018.03 和 lFE =0.005 m 文件 0018.04-0018.05
- 考虑几何线性分析
- 增量的数量是10
- 杆件的抗剪刚度被忽略
结果输出
| 型号 | 解析解 | RFEM 5 | RFEM 6 | ||
| uz,max [mm] | uz,max [mm] | 比率 [-] | uz,max [mm] | 比率 [-] | |
| 一维各向同性塑性 | 85,999 | 86,215 | 1,003 | 86,139 | 1,002 |
| 二维各向同性非线性弹性弹性板 | 86,566 | 1,007 | 86,431 | 1,005 | |
| 二维/三维各向同性塑性，板 | 84,142 | 0,978 | 84,142 | 0,978 | |
| 二维各向同性非线性弹性弹性板，可变厚度 | 83,728 | 0,974 | 83,121 | 0,967 | |
| 二维/三维各向同性塑性，板，可变厚度 | 83,088 | 0,966 | 83,088 | 0,966 | |
| 一维各向同性非线性弹性 | 86,215 | 1,003 | 86,136 | 1,002 | |
Dlubal_KohlA_]_LI.jpg?mw=350&hash=ee8d38f1c4853d80307fa156c159b5e78a3fdca9)
