Beschreibung
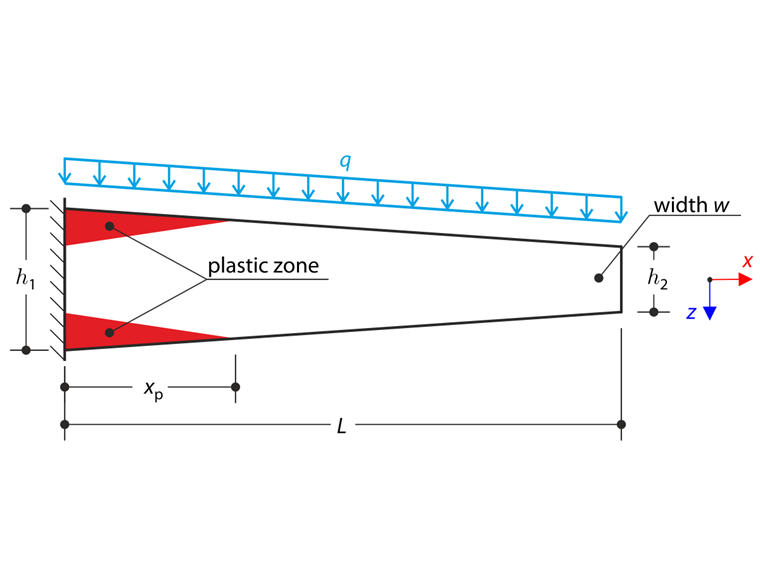
Am linken Ende ist ein Voutenkragarm vollflächig befestigt und mit einer Dauerlast q belastet. In diesem Beispiel werden kleine Verformungen berücksichtigt und das Eigengewicht wird vernachlässigt. Das Problem wird durch folgenden Parametersatz beschrieben. Es soll die maximale Durchbiegung uz,max bestimmt werden.
| Material | Elastisch-Plastisch | Elastizitätsmodul | E | 210000,000 | MPa |
| Querdehnzahl | ν | 0,000 | <nowiki>-</nowiki> | ||
| Schubmodul | G | 105000,000 | MPa | ||
| Fließgrenze | fy | 40,000 | MPa | ||
| Geometrie | Kragarm | Länge | L | 4,000 | m |
| Breite | w | 0,005 | m | ||
| Höhe der linken Seite | h1 | 0,250 | m | ||
| Rechte Seitenhöhe | h2 | 0,150 | m | ||
| Last | Dauerlast | q | 2300,000 | N/m | |
Analytische Lösung
Dies ist eine komplexere Variante des Nachweisbeispiels 17. Dabei wird der verjüngte Kragarm berücksichtigt. Die Dauerlast q bewirkt den elastisch-plastischen Zustand der Platte. Das Berechnungsverfahren ist analog zum Nachweisbeispiel 17.
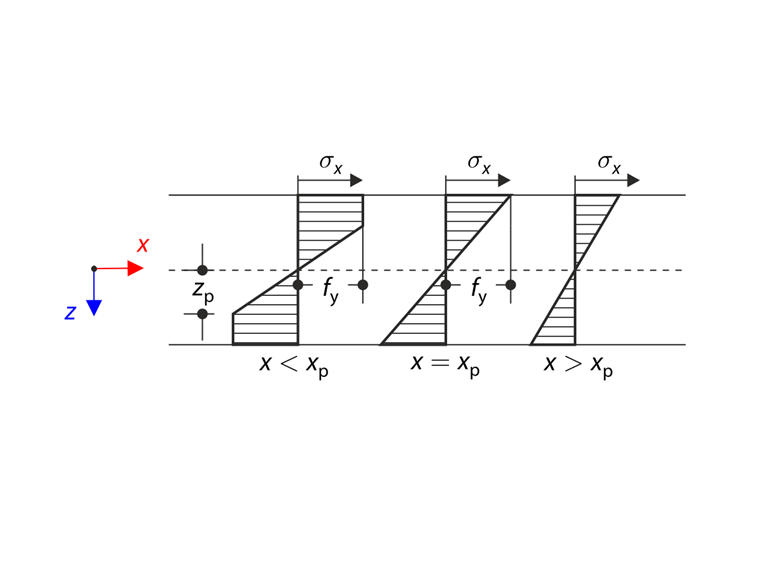
Das elastisch-plastische Moment Mep (Schnittgröße) muss gleich dem Biegemoment M (Fremdkraft) sein. Aus dieser Gleichheit resultiert die Krümmungp in der elastisch-plastischen Zone.
Die Gesamtdurchbiegung des Tragwerks wird als Überlagerung des elastisch-plastischen und des elastischen Beitrags über das Mohr-Integral definiert.
RFEM-Einstellungen
- Modelliert in RFEM 5.26 und RFEM 6.02
- Die Elementgröße beträgt lFE =0,020 m für die Dateien 0018.01-0018.03 und lFE =0,005 m für die Dateien 0018.04-0018.05
- Theorie I. Ordnung wird berücksichtigt.
- Die Anzahl der Inkremente beträgt 10
- Die Schubsteifigkeit der Stäbe wird vernachlässigt.
Ergebnisse
| Modell | Analytische Lösung | RFEM 5 | RFEM 6 | ||
| uz,max [mm] | uz,max [mm] | Ausnutzung [-] | uz,max [mm] | Ausnutzung [-] | |
| Isotrop plastisch 1D | 85,999 | 86,215 | 1,003 | 86,139 | 1,002 |
| Isotrop nichtlinear elastisch 2D, Platte | 86,566 | 1,007 | 86,431 | 1,005 | |
| Isotrop plastisch 2D/3D, Platte | 84,142 | 0,978 | 84,142 | 0,978 | |
| Isotrop nichtlinear elastisch 2D, Platte, Dicke veränderlich | 83,728 | 0,974 | 83,121 | 0,967 | |
| Isotrop plastisch 2D/3D, Platte, Dicke variable | 83,088 | 0,966 | 83,088 | 0,966 | |
| Isotrop nichtlinear elastisch 1D | 86,215 | 1,003 | 86,136 | 1,002 | |
Dlubal_KohlA_]_LI.jpg?mw=350&hash=ee8d38f1c4853d80307fa156c159b5e78a3fdca9)
