Description
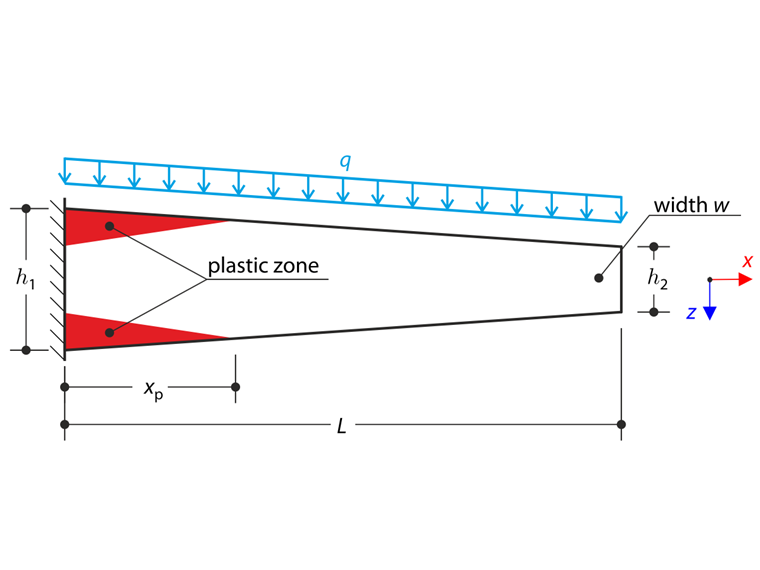
A tapered cantilever is fully fixed on the left end and subjected to a continuous load q. Small deformations are considered and the self-weight is neglected in this example. The problem is described by the following set of parameters. Determine the maximum deflection uz,max.
| Material | Elastic-Plastic | Modulus of Elasticity | E | 210000.000 | MPa |
| Poisson's Ratio | ν | 0.000 | - | ||
| Shear Modulus | G | 105000.000 | MPa | ||
| Yield Strength | fy | 40.000 | MPa | ||
| Geometry | Cantilever | Length | L | 4.000 | m |
| Width | w | 0.005 | m | ||
| Left Side Height | h1 | 0.250 | m | ||
| Right Side Height | h2 | 0.150 | m | ||
| Load | Continuous Load | q | 2300.000 | N/m | |
Analytical Solution
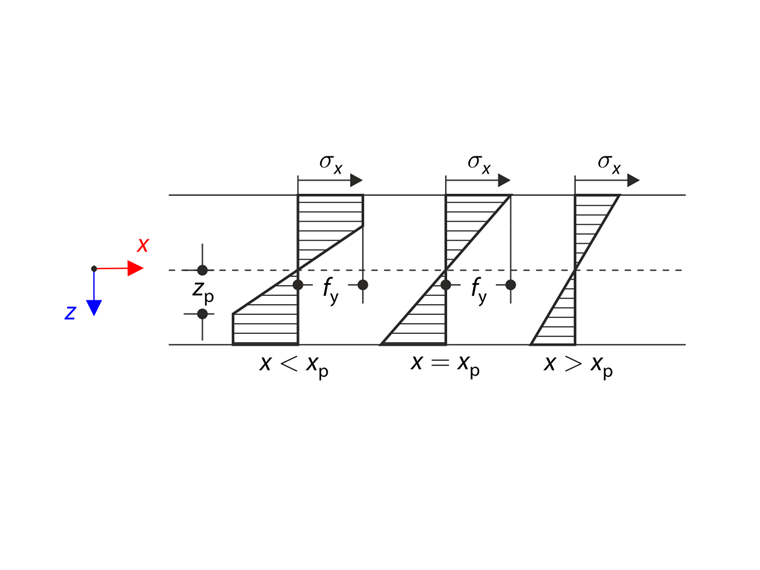
This is more complex variant of the verification example 17. The tapered cantilever is considered in this case. The continuous load q causes the elastic-plastic state of the plate. The calculation procedure is similar to verification example 17.
The elastic-plastic moment Mep (internal force) has to equal to the bending moment M (external force). The curvature κp in the elastic-plastic zone results from this equality.
The total deflection of the structure is defined as a superposition of the elastic-plastic and the elastic contribution using the Mohr's integral.
RFEM Settings
- Modeled in RFEM 5.26 and RFEM 6.02
- The element size is lFE=0.020 m for files 0018.01-0018.03 and lFE=0.005 m for files 0018.04-0018.05
- Geometrically linear analysis is considered
- The number of increments is 10
- Shear stiffness of the members is neglected
Results
| Model | Analytical Solution | RFEM 5 | RFEM 6 | ||
| uz,max [mm] | uz,max [mm] | Ratio [-] | uz,max [mm] | Ratio [-] | |
| Isotropic Plastic 1D | 85.999 | 86.215 | 1.003 | 86.139 | 1.002 |
| Isotropic Nonlinear Elastic 2D, Plate | 86.566 | 1.007 | 86.431 | 1.005 | |
| Isotropic Plastic 2D/3D, Plate | 84.142 | 0.978 | 84.142 | 0.978 | |
| Isotropic Nonlinear Elastic 2D, Plate, Variable Thickness | 83.728 | 0.974 | 83.121 | 0.967 | |
| Isotropic Plastic 2D/3D, Plate, Variable Thickness | 83.088 | 0.966 | 83.088 | 0.966 | |
| Isotropic Nonlinear Elastic 1D | 86.215 | 1.003 | 86.136 | 1.002 | |
Dlubal_KohlA_]_LI.jpg?mw=350&hash=ee8d38f1c4853d80307fa156c159b5e78a3fdca9)
