在RFEM和RSTAB中计算等效荷载

Mit RF-/DYNAM Pro Ersatzlasten ist es möglich, eine Ersatzlastberechnung anhand des multimodalen Antwortspektren-Verfahrens zu durchzuführen. Im dargestellten Beispiel wurde dies für einen Mehrmassenschwinger durchgeführt.

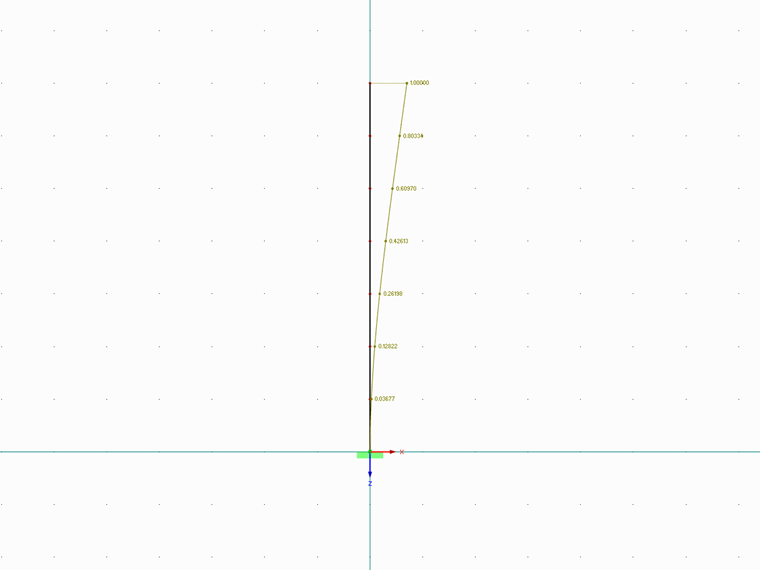
悬臂梁节点被细分为七个节点。在计算中使用了系统的第一个特征量确定了等效荷载和在各个节点上的分布。所需的固有频率和相应的等效质量系数通过RF-/DYNAM Pro Natural Vibrations确定。

示例

本文中的系统应该是一个约束柱，截面由HEB 500断面组成，高度为7 m。杆件上有七个对其施加自重的质量点。

可视化七个质量节点的悬臂梁

质量分布可以通过下面的矢量来描述：

m = (\begin{matrix} 1.000 \\ 1.000 \\ 1.000 \\ 1.000 \\ 1.000 \\ 1.000 \\ 1.000 \end{matrix})

m	Masse in kg

质量分布向量

固有振动分析的结果如下。

1. 固有频率f = 4.65 Hz
相应的周期长度t = 0.215 s
等效质量系数f_me，x = 0.667
沿结构高度上向量符号的归一化变形。

规范化变形

现在，该结构的光谱加速度为0.25 m/s²。第一个固有频率的等效质量系数和相应的频谱加速度可以用于计算地震总力。

H_{e, tot} = m_{Gesamt} \cdot f_{me, x} \cdot S_{d} (T_{1}) = 1, 167 kN

H_e,tot	Gesamterdbebenkraft in kN
m_Gesamt	Gesamtmasse in t
f_me,x	Ersatzmassenfaktor
S_d(T₁)	Beschleunigung aus Antwortspektrum für die erste Eigenform zur Periodenlänge T₁ in m/s²