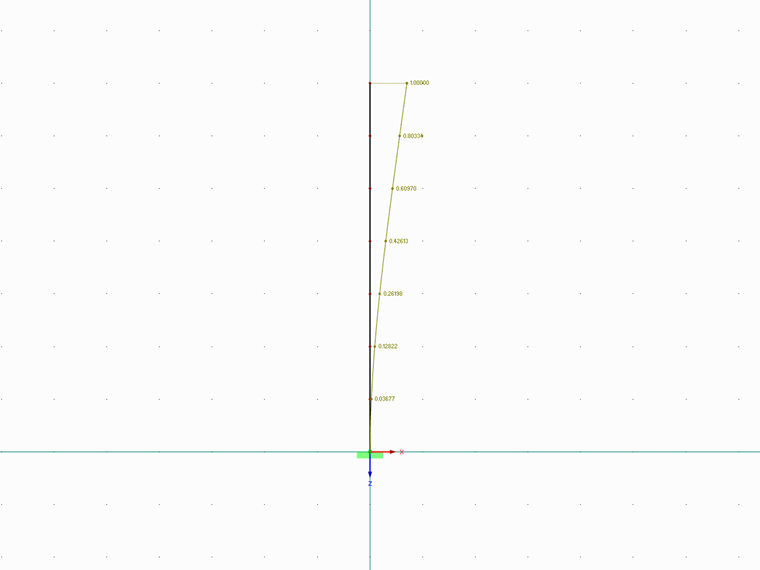
Pour ce faire, le porte-à-faux a été divisé en sept nœuds. Dans le calcul, la charge équivalente et la distribution sur les nœuds individuels ont été déterminées avec le premier vecteur propre du système. La fréquence propre requise et le facteur de masse équivalente correspondant ont été déterminés avec RF-/DYNAM Pro Natural Vibrations.
Exemple
Le système considéré doit être un poteau encastré constitué d'un profilé HEB 500 et d'une hauteur de 7 m. Le poids propre est appliqué à la barre.
La distribution des masses peut être décrite avec le vecteur suivant:
Les résultats de l'analyse des vibrations naturelles sont les suivants.
1. Fréquence propre f = 4,65 Hz
Durée de période correspondante t = 0,215 s
Facteur de masse équivalent fme, x = 0,667
Déformation normalisée en notation vectorielle sur la hauteur de la structure.
On suppose maintenant une accélération spectrale de 0,25 m/s² pour cette structure. Le facteur de masse équivalente de la première fréquence propre et l'accélération spectrale correspondante peuvent être utilisés pour déterminer la force sismique totale.
|
He,tot |
Gesamterdbebenkraft in kN |
|
mGesamt |
Gesamtmasse in t |
|
fme,x |
Ersatzmassenfaktor |
|
Sd(T1) |
Beschleunigung aus Antwortspektrum für die erste Eigenform zur Periodenlänge T1 in m/s2 |
À partir de cette force sismique totale, il est possible de calculer une contribution des points de masse pour la charge sismique totale à l'aide du déplacement normalisé.
|
λ |
Verteilungsfaktor |
|
si |
Verschiebung der Massen |
|
mi |
Gesamtmasse in kg |
|
sj |
Verschiebung der Massen in jedem Geschoss |
|
mj |
Stockwerksmassen in kg |
À l'aide de la distribution de la charge totale, vous pouvez désormais calculer les charges nodales.
|
He |
Knotenlast in jedem Stockwerk |
|
He,tot |
Gesamterdbebenlast in kN |
|
λ |
Verteilungsfaktor für jedes Geschoss |