Volver a la base de datos de conocimientos
¿Le ha resultado útil esta página?
3478x
000468
Dipl.-Ing. (FH) Stefan Frenzel
2021-01-28

Determinación de cargas equivalentes en RFEM y RSTAB

Mit RF-/DYNAM Pro Ersatzlasten ist es möglich, eine Ersatzlastberechnung anhand des multimodalen Antwortspektren-Verfahrens zu durchzuführen. En el ejemplo que se muestra aquí, esto se hizo para un oscilador de masas múltiples.

Para este propósito, el voladizo se subdividió en siete nudos. En el cálculo, la carga equivalente y la distribución en los nudos individuales se han determinado con el primer vector propio del sistema. La frecuencia natural necesaria y el factor de masa equivalente correspondiente se determinaron con RF-/DYNAM Pro Natural Vibrations.

Ejemplo

El sistema considerado debería ser un pilar coaccionado que consta de un perfil HEB 500 y tiene una altura de 7 m. La barra tiene siete puntos de masa a los que se aplica el peso propio.

Visualización del voladizo con siete nudos de masa
Visualización del voladizo con siete nudos de masa

La distribución de las masas se puede describir con el siguiente vector:

m = 1.0001.0001.0001.0001.0001.0001.000

m

Masse in kg
Vector de distribución masiva

Los resultados del análisis de vibraciones naturales son los siguientes.

1. Frecuencia natural f = 4,65 Hz
Longitud del periodo correspondiente t = 0,215 s
Factor de masa equivalente fme, x = 0,667
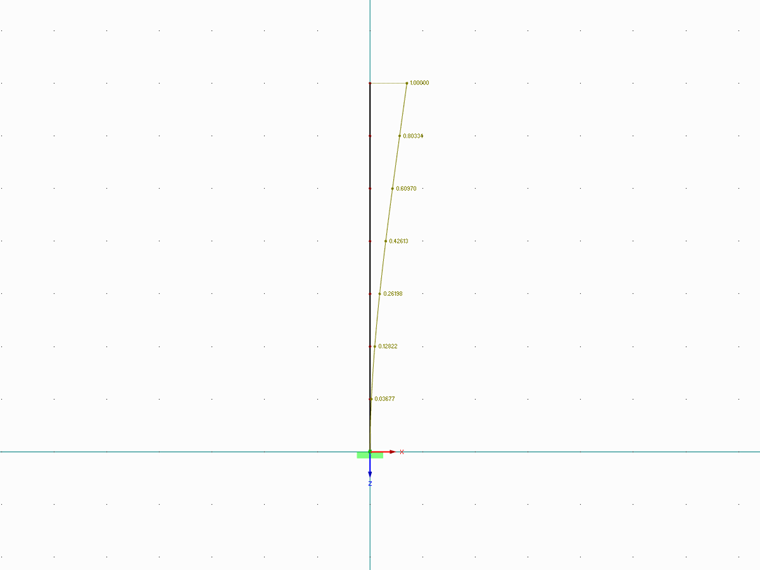
Deformación normalizada en notación vectorial sobre la altura de la estructura.

Deformación normalizada
Deformación normalizada

Ahora, se supone una aceleración espectral de 0,25 m/s² para esta estructura. El factor de masa equivalente de la primera frecuencia natural y la aceleración espectral correspondiente se pueden usar para determinar la fuerza sísmica total.

He,tot = mGesamt · fme,x · SdT1 = 1,167 kN

He,tot

Gesamterdbebenkraft in kN

mGesamt

Gesamtmasse in t

fme,x

Ersatzmassenfaktor

Sd(T1)

Beschleunigung aus Antwortspektrum für die erste Eigenform zur Periodenlänge T1 in m/s2 
esfuerzo de cortante de base

A partir de esta fuerza sísmica total, es posible calcular una contribución de los puntos de masa para la carga sísmica total por medio del desplazamiento normalizado.

λ = si · mi∑sj · mj

λ

Verteilungsfaktor

si

Verschiebung der Massen

mi

Gesamtmasse in kg

sj

Verschiebung der Massen in jedem Geschoss

mj

Stockwerksmassen in kg
Coeficiente de distribución de masas

Usando la distribución de la carga total, ahora también puede calcular las cargas en los nudos.

He = He,tot · λ = 0,360,290,220,150,090,050,01

He

Knotenlast in jedem Stockwerk

He,tot

Gesamterdbebenlast in kN

λ

Verteilungsfaktor für jedes Geschoss
Cargas sísmicas en nudos

Cargas sísmicas distribuidas sobre nudos de masa
Cargas sísmicas distribuidas sobre nudos de masa

ES | Bandera Base de datos de conocimientos
KB 000468 | Determinación de cargas equivalentes en RFEM y RSTAB
Autor

El Sr. Frenzel es responsable del desarrollo de productos para el análisis dinámico. También proporciona soporte técnico para los clientes de Dlubal Software.

Enlaces
  • Mia: asistente de IA
  • Última base de datos de conocimientos
Eventos
Vídeos
Modelos para descargar
Artículos de la base de datos de conocimientos
Visualización de un procedimiento para realizar un análisis de estabilidad según DIN EN 1992-1-1 en RFEM 6
Para componentes y estructuras de hormigón armado cuyo comportamiento estructural se ve afectado significativamente por los efectos según el análisis de segundo orden, el Eurocódigo 2 proporciona un método general basado en una determinación no lineal de los esfuerzos internos según el análisis de segundo orden (5.8.6), así como un método de aproximación basado en la curvatura nominal (5.8.8).

El objetivo de este artículo técnico es realizar un cálculo según el método general de cálculo del Eurocódigo 2 utilizando un ejemplo de un pilar de hormigón armado.
Modell eines Stahlbetonbalkens, der durch Kriechen und Schwinden beeinflusst wird
Este artículo técnico trata sobre el análisis de deformación directa de una viga de hormigón armado, teniendo en cuenta los efectos a largo plazo de la fluencia y la retracción. Se utiliza una viga de vano simple para explicar el cálculo directo según el Eurocódigo 2 (EN 1992-1-1, cláusula 7.4.3). Se presta especial atención a la rigidez a tracción, el comportamiento en el estado fisurado sobre la base del factor de distribución (parámetro de daño) y la consideración del comportamiento de la retracción y la fluencia.
Modelo que muestra uniones de acero integradas destacando la interacción entre la conexión y la estructura en el diseño
Este artículo explora la importancia de considerar la interacción unión-estructura en el modelado y diseño y cómo hacerlo en RFEM 6.
Illustration of equivalent lateral force method for seismic analysis in structural engineering
Este artículo proporciona una visión general completa de los métodos de análisis sísmico esenciales, explicando sus principios y aplicaciones, así como los escenarios en los que son más eficaces.
Capturas de pantalla
Características de los productos
Modelo de material anisótropo

En el complemento 'Comportamiento no lineal del material', puede usar el Modelo de material anisótropo para componentes de hormigón | Daño" del material para componentes estructurales de hormigón. Este modelo de material le permite considerar el daño del hormigón para barras, superficies y sólidos.

Puede definir un diagrama tensión-deformación individual a través de una tabla, usar la entrada paramétrica para generar el diagrama tensión-deformación o usar los parámetros predefinidos de las normas. Además, es posible considerar el efecto de la rigidez a tracción.

Para la armadura, están disponibles ambos modelos de material no lineal "Isótropo | Plástico (barras)" e "Isótropo | Elástico no lineal (barras)".

Es posible considerar los efectos a largo plazo debidos a la fluencia y retracción utilizando el "Análisis estático | Fluencia y retracción (lineal)" que se ha publicado recientemente. La fluencia se tiene en cuenta estirando el diagrama tensión-deformación del hormigón por el factor (1+phi) y la retracción como la predeformación del hormigón. Es posible realizar análisis de pasos de tiempo más detallados utilizando el complemento "Análisis dependiente del tiempo (TDA)".

Característica 002918 | Determinación de la armadura longitudinal necesaria para el análisis directo de fisuras

En el complemento Cálculo de hormigón, puede determinar la armadura longitudinal necesaria para el cálculo directo de las aberturas de fisura (wk).

Característica 002920 | Función automática de armadura longitudinal en barras

Para el diseño de barras de hormigón armado, hay una opción para determinar automáticamente el número o el diámetro de las barras de armadura.

Característica 002916 | Interacción unión-estructura para uniones de acero

¿Le gustaría considerar automáticamente la rigidez de las uniones de acero en su modelo global de RFEM? ¡Entonces use el complemento Uniones de acero!

Simplemente active la interacción unión-estructura en el análisis de rigidez de sus uniones de acero. Con esto las articulaciones con muelles se generan automáticamente en el modelo global y se tienen en cuenta en los cálculos posteriores.

Preguntas más frecuentes (FAQs)

En el complemento de Uniones de acero obtengo índices de aprovechamiento elevados para tornillos pretensados para la comprobación de esfuerzo a tracción. ¿De dónde proviene este alto aprovechamiento y cómo puedo evaluar las reservas de capacidad de carga del tornillo?

¿Cómo puedo comprender el cálculo de la armadura necesaria?

¿Cómo puede tratar una conexión como rígida resultar en un diseño poco económico?

¿Es posible considerar paneles de cortante y coacciones al giro también en el cálculo global?
Una unión de acero en mi modelo no es calculable. ¿Cómo puedo obtener más información para encontrar la causa?
Estoy calculando un pilar que está coaccionado en la base, sujeto en la cabeza en la dirección X y puede pandear en la dirección Y. He establecido las longitudes eficaces utilizando apoyos en nudos. En el cálculo, los valores de las longitudes eficaces para el cálculo son ambos iguales L_ (cr, z) = L_ (cr, y) = 2,41 m. ¿Qué he hecho mal?
Proyectos de clientes
Productos recomendados para usted
Mostrar familia de productos