A tale scopo, lo sbalzo è stato suddiviso in sette nodi. Nel calcolo, il carico equivalente e la distribuzione sui singoli nodi sono stati determinati con il primo autovettore del sistema. La frequenza naturale richiesta e il coefficiente di massa equivalente corrispondente sono stati determinati con RF-/DYNAM Pro Natural Vibrations.
Esempio
Il sistema considerato dovrebbe essere una colonna vincolata che consiste in un profilo HEB 500 ed è alta 7 m. L'asta ha sette punti di massa a cui si applica il peso proprio.
La distribuzione delle masse può essere descritta con il seguente vettore:
I risultati dell'analisi delle vibrazioni naturali sono i seguenti.
1. Frequenza naturale f = 4,65 Hz
Lunghezza del periodo corrispondente t = 0,215 s
Coefficiente di massa equivalente fme, x = 0,667
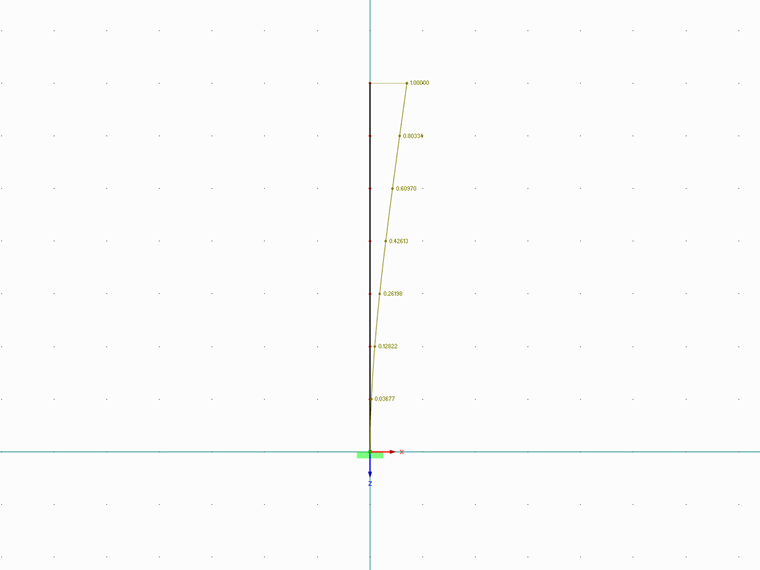
Deformazione normalizzata in notazione vettoriale sopra l'altezza della struttura.
Ora, si assume un'accelerazione spettrale di 0,25 m/s² per questa struttura. Il coefficiente di massa equivalente della prima frequenza naturale e la corrispondente accelerazione spettrale possono essere utilizzati per determinare la forza totale del terremoto.
|
He,tot |
Gesamterdbebenkraft in kN |
|
mGesamt |
Gesamtmasse in t |
|
fme,x |
Ersatzmassenfaktor |
|
Sd(T1) |
Beschleunigung aus Antwortspektrum für die erste Eigenform zur Periodenlänge T1 in m/s2 |
Da questa forza sismica totale, è possibile calcolare un contributo dei punti di massa per il carico sismico totale mediante lo spostamento normalizzato.
|
λ |
Verteilungsfaktor |
|
si |
Verschiebung der Massen |
|
mi |
Gesamtmasse in kg |
|
sj |
Verschiebung der Massen in jedem Geschoss |
|
mj |
Stockwerksmassen in kg |
Utilizzando la distribuzione del carico totale, è ora possibile calcolare anche i carichi nodali.
|
He |
Knotenlast in jedem Stockwerk |
|
He,tot |
Gesamterdbebenlast in kN |
|
λ |
Verteilungsfaktor für jedes Geschoss |