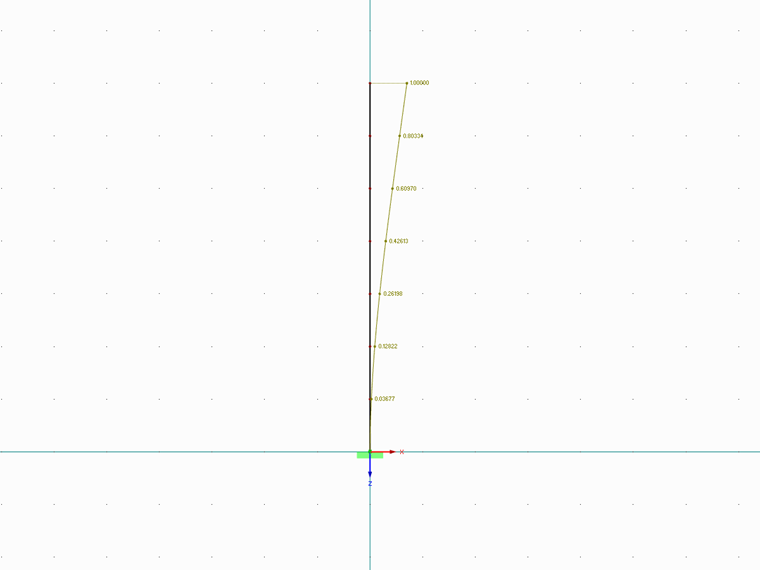
For this purpose, the cantilever was subdivided into seven nodes. In the calculation, the equivalent load and the distribution on the individual nodes were determined with the first eigenvector of the system. The required natural frequency and the corresponding equivalent mass factor were determined with RF-/DYNAM Pro Natural Vibrations.
Example
The system considered should be a restrained column that consists of an HEB 500 profile and is 7 m high. The member has seven mass points to which the self-weight is applied.
The distribution of the masses can be described with the following vector:
The results of the natural vibration analysis are as follows.
1. Natural frequency f = 4.65 Hz
Corresponding period length t = 0.215 s
Equivalent mass factor fme,x = 0.667
Normalized deformation in vector notation over the height of the structure.
Now, a spectral acceleration of 0.25 m/s² is assumed for this structure. The equivalent mass factor of the first natural frequency and the corresponding spectral acceleration can be used to determine the total earthquake force.
|
He,tot |
Gesamterdbebenkraft in kN |
|
mGesamt |
Gesamtmasse in t |
|
fme,x |
Ersatzmassenfaktor |
|
Sd(T1) |
Beschleunigung aus Antwortspektrum für die erste Eigenform zur Periodenlänge T1 in m/s2 |
From this total earthquake force, it is possible to calculate a contribution of the mass points for the total seismic load by means of the normalized displacement.
|
λ |
Verteilungsfaktor |
|
si |
Verschiebung der Massen |
|
mi |
Gesamtmasse in kg |
|
sj |
Verschiebung der Massen in jedem Geschoss |
|
mj |
Stockwerksmassen in kg |
Using the distribution of the total load, you can now also calculate the nodal loads.
|
He |
Knotenlast in jedem Stockwerk |
|
He,tot |
Gesamterdbebenlast in kN |
|
λ |
Verteilungsfaktor für jedes Geschoss |