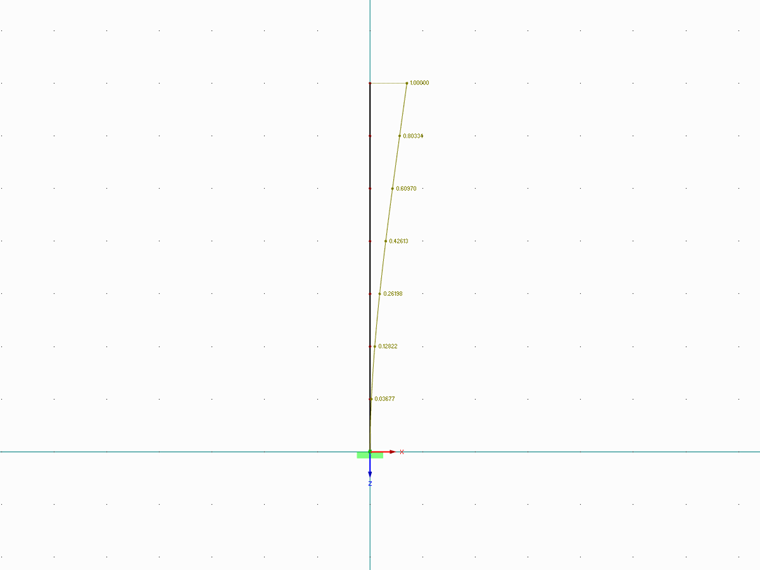
Vetknutý sloup byl rozdělen do sedmi uzlů. Při výpočtu byla stanovena náhradní zatížení a jejich rozložení v jednotlivých uzlech pro první vlastní tvar. Požadované vlastní frekvence a odpovídající modální hmoty byly stanoveny pomocí modulu RF-/DYNAM Pro Natural Vibrations.
Příklad
Uvažovaný systém je vetknutý sloup z profilu HEB 500 vysoký 7 metrů. Na prutu je 7 hmotných bodů, v nichž působí vlastní tíha.
Rozložení hmot lze popsat následujícím vektorem:
Výsledky analýzy vlastního kmitání jsou následující.
1. vlastní frekvence f = 4,65 Hz
příslušná perioda t = 0,215 s
faktor účinných modálních hmot fme,x = 0,667
normalizovaná deformace ve vektorovém zápisu podél výšky konstrukce.
Nyní předpokládejme pro tuto konstrukci spektrální zrychlení 0,25 m/s² po celou periodu. Pomocí faktoru účinných modálních hmot první vlastní frekvence a tomu odpovídajícímu spektrálnímu zrychlení lze stanovit celkovou smykovou seizmickou sílu.
|
He,tot |
Gesamterdbebenkraft in kN |
|
mGesamt |
Gesamtmasse in t |
|
fme,x |
Ersatzmassenfaktor |
|
Sd(T1) |
Beschleunigung aus Antwortspektrum für die erste Eigenform zur Periodenlänge T1 in m/s2 |
Z této celkové smykové seizmické síly lze pomocí normovaného posunu vypočítat příspěvek hmotných bodů pro celkové seizmické zatížení.
|
λ |
Verteilungsfaktor |
|
si |
Verschiebung der Massen |
|
mi |
Gesamtmasse in kg |
|
sj |
Verschiebung der Massen in jedem Geschoss |
|
mj |
Stockwerksmassen in kg |
Z rozdělení celkového zatížení lze nyní vypočítat také uzlová zatížení.
|
He |
Knotenlast in jedem Stockwerk |
|
He,tot |
Gesamterdbebenlast in kN |
|
λ |
Verteilungsfaktor für jedes Geschoss |